Determinarea indicilor de dispersie

DETERMINAREA INDICILOR DE DISPERSIE

Media, mediana si modul caracterizeaza un singur aspect al distributiei statistice: tendinta generala a datelor. Este necesar sa cunoastem si modul in care se repartizeaza diferite rezultate in jurul 'valorii centrale', adica organizarea interioara a distributiei. De exemplu, doua distributii statistice - cum sunt cele redate in figura 3.1. - pot avea aceeasi medie, dar ele sa fie totusi foarte diferite sub aspectul variabilitatii, respectiv al omogenitatii.

Figura 3.1.

Se pune deci problema de a gasi indicatori prin intermediul carora se poate masura variatia sau imprastierea datelor in jurul mediei. Acesti indicatori sunt: dispersia sau varianta, si abaterea standard.Cu ajutorul lor se obtin informatii asupra variabilitatii grupului studiat.

Dispersia si abaterea standard

Dispersia sau varianta se noteaza cu σ² sau cu s² si are ca formula de definiitie:

in care (x-m) reprezinta abaterea fiecarei valori de la media calculata, iar N este efectivul grupei de masurari.

Abaterea standard sau abaterea tip - care se noteaza cu σ sau cu s - nu este altceva decat radacina patrata din valoarea dispersiei: Asadar, pentru a determina abaterea standard trebuie oricum sa aflam mai intai dispersia σ².

Indicele de dispersie cel mai exact si mai des utilizat este de fapt abaterea standard, avand avantajul de a fi exprimat in aceleasi unitati ca si datele initiale pe care le prelucram. De exemplu, daca studiul se bazeaza pe note, abaterea standard este exprimata tot in note, permitand sa se analizeze mai corect gradul de variabilitate al grupului.

Abaterea tip se foloseste, de asemenea, in discutarea distributiilor normale. Dispersia are avantajul de a nu cuprinde radicalul in expresia ei algebrica si astfel se preteaza mai usor la calcule teoretice.

Daca analizam formula de definitie a dispersiei ne dam seama ca numai expresia de la numarator, adica suma patratelor abaterilor de la medie, ridica probleme mai dificile pentru calcul. Vom numi pe scurt aceasta expresie suma patratelor.

Determinarea sumei patratelor nu se face utilizand expresia de definitie Σ(x-m)² deoarece comporta operatii laborioase si de cele mai multe ori cu numere zecimale. Transformand expresia de definitie, se obtine o formula convenabila de calcul:

in care notatiile sunt deja cunoscute. Σx² reprezinta totalul patratelor celor N rezultate (valori) care compun grupul initial de date.

Formula de calcul a dispersiei devine astfel:

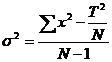
De notat ca T² si Σx² sunt valori cu totul diferite, ceea ce se poate verifica in tabelul 3.3.

In ceea ce priveste determinarea disprsiei, avand datele grupate, ne referim din nou la cele doua metode utilizate pentru calculul mediei.

Metoda de calcul ilustrata prin tabelul 3.3, ne-a condus la determinarea lui T prin insumarea produselor fxx, stiind ca Σfxx'T. Ridicand acum la patrat pe T si impartind apoi cu N (efectivul grupei), avem stabilit T²/N din formula de calcul a sumei patratelor stabilita mai sus. Ne ramane sa calculam doar Σx². Pentru aceasta la tabelul care a condus la determinarea lui T mai adaugam o coloana fxx² in care vom inscrie produsele (fxx) x x (adica produsele fxx notate in coloana precedenta se mai inmultesc o data cu valorile x).

Pentru ilustrare sa urmarim exemplul din tabelul 3.3.

Tabelul 3.3.

Insumand produsele inscrise in coloana (f x x) x x sau, pe scurt fxx², se obtine Σx² si in felul acesta avem asigurate toate elementele necesare pentru determinare sumei patratelor potrivit formulei.

Exemplul ales constituie oarecum un caz particular, avand ca interval de grupare i = 1. Valorile centrale x_k coincid cu valorile lui x. Aceasta este situatia seriilor de variatie mai mici, cand distanta dintre valorile extreme nu este mai mare si permite o grupare mai simpla a datelor (de pilda, in cazul notelor scolare).

Cand intervalul de grupare este mai mare decat 1 si lucram cu valori centrale x_k, produsele vor fi fxx_xxx_k, adica fxx_k².

Facand inlocuirile necesare in exemplul dat vom avea:

Pentru a determina dispersia sau varianta, impartim rezultatul obtinut la N - 1.

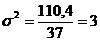
In continuare extragem radacina patrata din σ² sau s² si obtinem abaterea tip:

Se poate observa ca pentru determinarea dispersiei in tabelul de calcul utilizat la medie se adauga doar inca o coloana fxx². Pentru usurarea caculelor trebuie utilizate tabele matematice uzuale, care ne dau n² si pentru orice numere pana la 10.000.

_{In incheiere sunt necesare doua precizari esentiale:}

● In prezent, determinarea indicilor statistici se face cu ajutorul calculatorului, care preia munca de rutina a cercetatorului. Acesta din urma decide insa ce indici va calcula, ce tabele si grafice sunt necesare in functie de natura datelor, va intrevedea forma distributiei si obiectivele cercetarii. Programele informatice aplicate vor sugera modul in care trebuie pregatit si organizat materialul brut pentru prelucrarea statistica; psihologul - cercetator stapaneste datele de intrare si 'citeste' datele de iesire pe care le interpreteaza.

● Datele numerice sunt culese pe loturi sau grupuri extrase dintr-o colectivitate mai larga numita populatie. Elementele unui lot sau grup trebuie alese dupa regulile selectiei aleatoare pentru a putea formula concluzii valabile. Notam indicii obtinuti pe esantion cu si respectiv cu