ESTIMAREA MEDIEI ARITMETICE CAND σ ESTE CUNOSCUT

Atunci cand se estimeaza un punct, se alcatuieste un esantion aleatoriu, se calculeaza o medie aritmetica sau o proportie si se estimeaza ca valoarea parametrului respectiv este egala cu valoarea calculata pentru esantion. In acest tip de estimare se tine cont faptul ca eficienta estimatorului este direct proportionala cu dimensiunea esantionului, ceea ce inseamna ca probabilitatea ca estimatorul sa fie aproximativ egal cu parametrul corespunzator este cu atat mai mare, cu cat dimensiunea esantionului este mai mare.

Procedura de estimare a intervalelor este relativ mai complicata, dar este mai sigura, in sensul ca, atunci cand se estimeaza un interval, probabilitatea ca in acel interval sa se afle parametrul de interes este mai mare si poate fi stabilita cu precizie.

Fie o populatie cu media aritmetica μ si cu abaterea standard σ. Selectam aleatoriu un esantion de dimensiune n din aceasta populatie si calculam media aritmetica pentru esantion, . Conform teoremei limitei centrale, distributia de esantionare a mediilor aritmetice ale tuturor esantioanelor posibile de dimensiune n din populatia de referinta este aproximativ normala, cu media aritmetica egala cu cea a populatiei de referinta si cu abaterea standard egala cu . Pe baza caracteristicilor distributiei de esantionare si a tabelului distributiei normale standard putem formula enunturi de probabilitate despre mediile aritmetice ale esantioanelor. De pilda, din tabel aflam ca proportia de cazuri (medii aritmetice ale esantioanelor) cuprinse intre Z = 1,96 si media aritmetica este de 0,475. Intrucat curba este simetrica, proportia de cazuri cuprinse intre Z = 1,96 si media aritmetica este tot de 0,475. Astfel, proportia de cazuri cuprinse intre 1,96 abateri standard fata de medie este de 0,95, iar proportia de cazuri aflate sub 1,96 si peste 1,96 abateri standard fata de medie este de 0,05 (0,025 + 0,025):

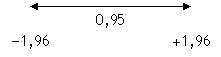
Acelasi lucru ca mai sus poate fi exprimat spunand ca 95% din mediile aritmetice ale esantioanelor se afla in intervalul dintre si  sau, pe scurt, in intervalul . Structura acestui tip de enunt de probabilitate poate fi folosita pentru a estima valoarea parametrului μ, prin construirea unui interval centrat pe valoarea cunoscuta pentru esantion, . Rezultatul este un interval de incredere estimat - o amplitudine de valori in care este probabil (nu sigur) sa se afle μ. Astfel, putem estima ca exista o probabilitate de 0,95 (sau 95%) ca media aritmetica a populatiei sa se afle in intervalul , ceea ce inseamna ca probabilitatea ca media aritmetica a populatiei sa nu se afle in acest interval este de 0,05 (sau 5%).

Probabilitatea ca media aritmetica a populatiei sa nu se afle in intervalul estimat sau, altfel spus, probabilitatea de eroare a estimarii se numeste nivel de semnificatie sau nivel alfa (α), iar probabilitatea ca intervalul estimat sa contina media aritmetica a populatiei se numeste nivel de incredere. Dupa cum reiese si din cele de mai sus, nivelul de incredere este complementarul nivelului alfa, fiind egal cu 1 α sau, in procente, cu (1 α) 100. A stabili, de pilda, ca α = 0,05 inseamna acelasi lucru cu a spune ca nivelul de incredere este de 95%. Intrucat probabilitatea de eroare este impartita in mod egal in extremitatea inferioara si cea superioara a distributiei de esantionare, stabilindu-se astfel limita inferioara si limita inferioara de incredere, vom nota scorul Z corespunzator nivelului α ales cu Z_α/2. Astfel, in cazul in care σ este cunoscut, formula de construire a unui interval de incredere estimat (IE) bazat pe media aritmetica a unui esantion este urmatoarea:

Formula 6.1

Ca exemplu, sa presupunem ca dorim sa estimam media aritmetica zilnica a orelor de vizionare a programelor TV de catre femeile casnice. Pentru aceasta, alcatuim un esantion aleatoriu de 200 de femei casnice (n = 200) si aflam ca acestea petrec in medie 6 ore pe zi vizionand programe TV (). Prin testari extensive stim ca abaterea standard a populatiei pentru vizionarea programelor TV este de aproximativ 0,7 (σ = 0,7). In aceasta cercetare suntem dispusi sa asumam o sansa de a gresi de 10%, stabilind α = 0,10. Pentru a determina limitele de incredere inferioara si superioara, trebuie sa scadem 0,05 (i.e. α/2) din 0,5 (proportia de cazuri aflate de o parte si de alta a mediei aritmetice a distributiei de esantionare). Rezultatul scaderii este 0,450, ceea ce reprezinta proportia de cazuri dintre o limita de incredere si medie:

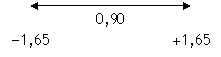
Astfel, pentru α = 0,10 trebuie sa cautam proportia 0,4500 in tabelul distributiei normale standard. Gasim insa o proportie de 0,4495, corespunzatoare scorului Z_α/2 = 1,64 si o proportie de 0,4505, corespunzatoare scorului Z_α/2 = 1,65. Scorul Z_α/2 pe care il cautam se afla undeva intre aceste doua scoruri. In aceste conditii, se ia cel mai mare dintre cele doua scoruri: 1,65. In acest fel, intervalul de incredere va fi cel mai mare posibil in circumstantele date. Prin urmare, vom avea:

6 1,65(0,7/14,14) =

= 6 1,65 0,0495 = 6 0,08

Pe baza mediei aritmetice a esantionului, estimam ca femeile casnice petrec in medie intre 5,92 (6 0,08) si 6,08 (6 0,08) ore pe zi vizionand programe TV. O alta modalitate de a enunta acest interval este 5,92 < μ < 6,08. Aceasta estimare are o sansa de 10% de a fi gresita, adica de a nu contine media aritmetica a populatiei.

In principiu, cercetatorul poate folosi orice valoare pentru nivelul de incredere. Totusi, nivelurile de incredere folosite in mod obisnuit sunt 90%, 95% si 99%. In cazul nivelului de incredere de 99% ne confruntam cu aceeasi problema ca in ultimul exemplu de mai sus. In acest caz, α = 0,01 si scazand 0,005 (α/2) din 0,5 obtinem 0,495. In tabel nu apare proportia 0,4950, dar apar proportiile 0,4949 (Z_α/2 = 2,57) si 0,4951 (Z_α/2 = 2,57). Ca mai sus, se ia cel mai mare dintre cele doua scoruri: 2,58. Tabelul urmator rezuma toate datele de care avem nevoie:

Tabelul 6.1 Niveluri de incredere si scoruri Z_α/2