Bacalaureat 2005 matematica – informatica m1 rezolvari

BACALAUREAT 2005 MATEMATICA – INFORMATICA M1 REZOLVARI

VARIANTA NR 3

SUBIECTUL I

1. 
2. 
3. 
4. Ecuatia nu are solutie
5. 
6. 
7. 
8. Numarul punctelor extrem este infinit
9. 
10. 

SUBIECTUL II

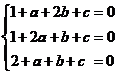
SUBIECTUL III

e.     Dimensiunea spatiului liniar este patru.Consideram matricele: Orice matrice patratica de ordinal doi este combinatie liniara a matricelor E,F,G,H In plus cele patru matrici formeaza un sistem liniar independent. Intradevar combinatia liniara aE+bF+cG+dH=O₂ este echivalenta cu sau adica a = b = c = d = 0. Sa aratam ca orice matrice este combinatie liniara a matriceloe E,F,G,H Evident

Functia f nu exte injectiva f Functia nu este surjectiva Presupunem ca este atunci oricare ar fi matricea Y din M₂ exista astfel incat AX-XA=Y rezulta Se obtine sau Se observa ca sistemul poate fi compatibil numai daca deci Z nu poate fi arbitrar.Ceea ce contrazice faptul ca f este surjectiva

SUBIECTUL IV

a.    

b.     In egalitatea precedenta rezulta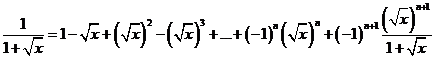

c.      Din si din >0 rezulta iar din

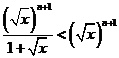
d. 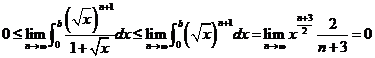    rezulta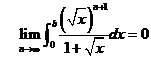

e.     Pentru calculul integralei amplificam fractia cu Rezulta 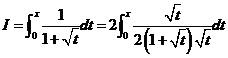Notam cu si obtinem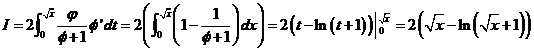

f.