
|
|
|
PUTERI SI RADICALI
Puteri cu exponent natural:
an unde aI|R, nI|N;
a0=1;
a1=a;
an
= ![]() ;
;
a - baza puterii;
n - exponentul puterii;
(ab)n=anbn, a,bI|R, nI|N*;
(am)n=amn, aI|R, m,nI|N*;
am an=am+n, aI|R, m,nI|N*;
![]() , b 0, a,bI|R, nI|N*;
, b 0, a,bI|R, nI|N*;
![]() , aI|R*, m,nI|N*, m>n.
, aI|R*, m,nI|N*, m>n.
Puteri cu exponent intreg negativ:
a-n=![]() unde aI|R*, nI|N;
unde aI|R*, nI|N;
restul proprietatilor se pastreaza.
Puteri cu exponent rational pozitiv:
![]() , a≥0,
, a≥0, ![]() Iℚ+;
Iℚ+;
![]() , a≥0,
, a≥0, ![]() ,
,![]() Iℚ+;
Iℚ+;
![]() , a,b≥0,
, a,b≥0, ![]() Iℚ+;
Iℚ+;
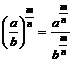 , a≥0, b>0,
, a≥0, b>0, ![]() Iℚ+;
Iℚ+;
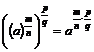 , a≥0,
, a≥0, ![]() ,
, ![]() Iℚ+;
Iℚ+;
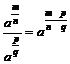 , a>0,
, a>0, ![]() ,
,![]() Iℚ+,
Iℚ+, ![]() >
>![]() .
.
Puteri cu exponent rational negativ:
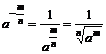 , a>0,
, a>0, ![]() Iℚ+;
Iℚ+;
restul proprietatilor se pastreaza.
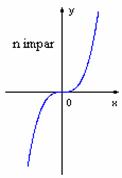
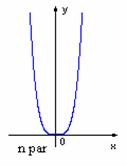 Functia putere cu exponent natural
nenul:
Functia putere cu exponent natural
nenul:
f(x)=xn, f:|R |R, nI|N*;
monotonia:
 ;
;
paritate:
![]() ;
;
semn: 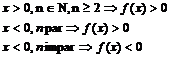 .
.
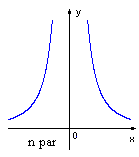
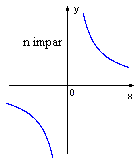 Functia putere cu exponent intreg
negativ:
Functia putere cu exponent intreg
negativ:
f(x)=x-n, f:|R- |R, nI|N*;
monotonia:
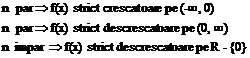 ;
;
paritate:
![]() ;
;
semn: 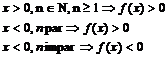 .
.
Functia putere cu exponent rational:
f(x)=![]() =
=![]() , f:(0, ) →(0, ),
, f:(0, ) →(0, ), ![]() Iℚ*;
Iℚ*;
daca
![]() >0 ⇒ f strict crescatoare;
>0 ⇒ f strict crescatoare;
daca ![]() <0 ⇒ f strict descrescatoare.
<0 ⇒ f strict descrescatoare.
Radicalul unui numar pozitiv:
ecuatia xn-a=0 (nI|N, n 2, aI|R, a>0) are o singura radacina reala pozitiva;
daca a>0, nI|N, n 2 se numeste radical de ordin n din a, numarul pozitiv a carui putere a n-a este a;
notatie
x=![]() ;
;
notatie
![]() =
=![]() ;
;
![]() =0;
=0;
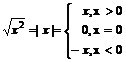 ;
;
Radicalul de ordin impar al unui numar negativ:
ecuatia xn-a=0 (nI|N, n 2, n impar, aI|R, a<0) are o singura radacina reala negativa;
daca a<0, nI|N, n 2, n impar, se numeste radical de ordin n din a, numarul negativ a carui putere a n-a este a;
notatie
x=![]() =
=![]() ;
;
Proprietatile radicalilor: m, n, kIℕ*, m, n, k≥2
P1) ![]() , a,b≥0;
, a,b≥0;
P2) ![]() , a≥0, b>0;
, a≥0, b>0;
P3) ![]() , a≥0;
, a≥0;
P4) (![]() )m =
)m =![]() , a≥0;
, a≥0;
P5) ![]() =
=![]() , a≥0;
, a≥0;
P6) ![]() , a≥0.
, a≥0.
Operatii cu radicali:
1. scoaterea unui factor de sub semnul radical: se descompune numarul de sub radical in factori, se aplica proprietatile 1, 3 si 5;
2. introducerea unui factor sub semnul radical: se utilizeaza proprietatile 1, 3 si 5;
3. inmultirea radicalilor de acelasi ordin sau ordine diferite: se utilizeaza proprietatea 1 si 5;
![]() , a1, a2, ., ak≥0;
, a1, a2, ., ak≥0;
![]() , a, b≥0;
, a, b≥0;
4. impartirea radicalilor de acelasi ordin sau ordine diferite: se utilizeaza proprietatile 2 si 5;
![]() , a≥0, b>0;
, a≥0, b>0;
![]() , a≥0, b>0;
, a≥0, b>0;
5. rationalizarea numitorilor
operatia de eliminare a radicalilor de la numitorul fractiilor;
expresii conjugate: - expresii cu radicali care prin inmultire dau o expresie fara radicali;
![]() , a, b≥0;
, a, b≥0;
![]() , a, b≥0;
, a, b≥0;
![]() , a, b≥0;
, a, b≥0;
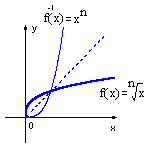
![]() , a, b≥0, n
impar;
, a, b≥0, n
impar;
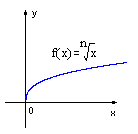 Functia radical:
Functia radical:
f(x)= ![]() , f:[0, [0, ), nI|N, n 2;
, f:[0, [0, ), nI|N, n 2;
monotonia: f strict crescatoare pe [0,
f(x) 0 xI[0,
functia este bijectiva;
inversa ei este functia putere.
f(x)= ![]() , f:|R |R, nI|N, n 2, n impar;
, f:|R |R, nI|N, n 2, n impar;
Ecuatii irationale:
ecuatii care contin necunoscuta sub semnul radical;
rezolvarea consta in eliminarea radicalilor prin diferite transformari (ridicari la putere = cu ordinul radicalului, inmultire cu expresia conjugata), reducandu-le la ecuatii studiate;
conditii
de existenta numai pentru radicali de ordin par ![]() : f(x)≥0 unde
f(x) este o expresie in functie de x;
: f(x)≥0 unde
f(x) este o expresie in functie de x;