Concursul de matematica al Revistei 'Arhimede' - Clasa a V-a

Concursul de matematica al Revistei 'Arhimede'

Clasa aV-a

I. 1 Puneti paranteze in expresia E=6·18+24:6+2 astfel incat rezultatul sa fie un numar natural cat mai mic.

2 Calculati: 2002³ - 2002² · 2001 - 2002 · 2000 - 1999.

II. Daca impartim un numar natural la 72 obtinem restul 68. Care este restul impartirii acelui numar la 24?

III. Determinati ultimele opt cifre ale numarului:A=1 · 2 · 3 · 4 · · 34 · 35.

IV. Calculati suma cifrelor numarului: B=4²⁰⁰² · 5⁴⁰⁰⁷ + 280.

Timp de lucru: 2 ore.

Fiecare subiect se noteaza cu 0-7 puncte.

Concursul de matematica al Revistei 'Arhimede'

Editia I, Bucuresti, 13-14 Decembrie 2003

Clasa aVI-a

I. 1 Determinati numarul natural n din egalitatea

2 Daca x, y, z sunt cifre nenule in baza 10, determinati numarul stiind ca A se divide cu 17.

II. Se considera multimea M

1) Comparati suma elementelor pare din multimea M cu suma elementelor impare din multimea M.

2) Se poate elimina un element din multimea M astfel incat suma elementelor pare ramase sa fie egala cu suma elementelor impare ramase?

III. Pe o dreapta d se iau punctele A, B, C,D astfel incat AB=a, BD=c, AC=b, BC=a+b, CD=a+b-c. Stabiliti ordinea punctelor A,B,C,D pe dreapta d.

IV. Aveti la dispozitie unghiuri cu masura de 17⁰. Descrieti un procedeu de a pune in evidenta un unghi cu masura de 3⁰.

Concursul de matematica al Revistei 'Arhimede'

Editia I, Bucuresti, 13-14 Decembrie 2003

Clasa aVII-a

I. Daca aIQ si bIQ astfel incat , calculati valoarea raportului

II. Fie a₁, a₂, a₃, , a₉ o scriere a numerelor naturale 1, 2, 3, , 9 intr-o alta ordine. Aratati ca numarul A a₁-1) · (a₂-1) ·(a₃-1) · ·(a₉-1) este par.

III. Fie M un punct in interiorul paralelogramului ABCD. Aratati ca se poate construi un patrulater convex xu aria egala cu jumatate din cea a paralelogramului ABCD si ale carui laturi au lungimile respectiv egale cu cele ale segmentelor MA, MB, MC, MD.

IV. 1) Aratati ca, intr-un triunghi, mediana corespunzatoare oricarei laturi este mai mica decat semisuma lungimilor celorlalte doua laturi.

2 In triunghiul ABC, (AD este bisectoarea unghiului A (DI (BC)). Paralela prin B la AD intersecteaza dreapta AC in E. Fie AM perpendiculara pe EB (MIEB). Aratati ca: MC 1/2·P_ABC (P_ABC este perimetrul triunghiului ABC).

Timp de lucru: 3 ore.

Fiecare subiect se noteaza cu 0-7 puncte.

Concursul de matematica al Revistei 'Arhimede'

Editia I, Bucuresti, 13-14 Decembrie 2003

Clasa aVIII-a

I. Fie aIR Q si bIRQ astfel incat a+bIQ. Aratati ca, oricare ar fi xIQ si yIQ, x y, avem a·x+b·yIR Q.

II. 1) Aratati ca, daca a, b,c sunt numere reale, atunci a²+b²+b² a·b+b·c+c·a.

2) Daca x, y, z sunt numere reale pozitive astfel incat x²+y²+z²=2, determinati cea mai mica valoare a expresiei

III. Cubul ABCDA'B'C'D' are muchia de lungime a. Punctul M apartine muchiei A'B' astfel incat distanta de la C' la dreapta MB este egala cu

IV. ABCD este un tetraedru in care AB BD si AC CD. E si F sunt mijloacele muchiilor [AD] si respectiv [BC]. Aratati ca, daca EF (BCD), atunci BD CD.

Timp de lucru: 3 ore.

Fiecare subiect se noteaza cu 0-7 puncte.

Concursul de matematica al Revistei 'Arhimede'

Editia I, Bucuresti, 13-14 Decembrie 2003

Clasa a IX-a

I. Fie a, b, c trei numere reale. Sa se demonstreze inegalitatile

1) a³+b³+b³ 3a·b·c daca a+b+c 0

2) (a²-b·c)³+ b²-a·c)³+ c²-a·b)³ 3 a²-b·c) b²-a·c) c²-a·b)

3) a⁴+b⁴+b⁴ a·b·c· (a+b+c)

* * *

II. Daca x₁, x₂, x₃, x₄ sunt numere reale strict pozitive, atunci

Sorin Radulescu si Marius Radulescu

III. Sa se determine valorile parametrului real m -1, astfel incat ecuatia

(m+1)· x²+x+m-1=0 sa admita cel putin o radacina intreaga.

Ana-Maria Petriceanu

IV. In triunghiul ABC, fie w centrul cercului lui Euler si   . Sa se calculeze in functie de urmatoarele sume

1)

2)

3)

(Revista Arhimede, nr. 1/2000)

Timp de lucru: 3 ore.

Fiecare subiect se noteaza cu 0-7 puncte.

Concursul de matematica al Revistei 'Arhimede'

Editia I, Bucuresti, 13-14 Decembrie 2003

Clasa a X-a

I. Fie z_k = (2·k+1)² +2·i, kIN^*. Sa se calculeze 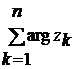nIN^*

(unde arg zI[0,2p) este argumentul numarului complex z

Costel Chites, D. Petriceanu

II. Se considera functiile: f, g: R R

Sa se demonstreze ca f si g sunt bijective.

Sorin Radulescu

III. Fie z₁, z₂ doua numere complexe. Sa se demonstreze ca

Marius Radulescu si Sorin Radulescu

IV. Determinati x, y numere reale stiind ca

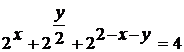
Dan Nedeianu (Revista Arhimede)

Timp de lucru: 3 ore.

Fiecare subiect se noteaza cu 0-7 puncte.