
|
|
|

![]()
Carl Friedrich Gauß, pictura de C.A. Jensen . Carl Friedrich Gauß, latinizat Carolo Friderico Gauss, (n.30 aprilie 1777, Braunschweig - d. 23 februarie 1855, Göttingen)
Carl Friedrich Gauss, el insusi cunoscut ca "print al matematicii", numea matematica "regina a stiintelor".
In latina - Regina Scientiarum, in germana - Königin der Wissenschaften. Ambele expresii sunt legate de cuvantul "stiinta" care inseamna (domeniu de) cunostinte. Intr-adevar, in acest sens, nu exista indoieli ca matematica este o stiinta. Restrangerea sensului de stiinta doar la domenii specializate care studiaza natura nu mai este de actualitate. Daca ar fi considerate stiinte doar acele domenii ale cunoasterii care se ocupa strict de lumea fizica, atunci matematica, sau cel putin matematica pura, ar trebui sa nu fie considerata o stiinta. Albert Einstein spunea ca "atunci cand legile matematicii se refera la realitate, ele nu sunt sigure iar cand sunt sigure, ele nu se refera la realitate" (as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality) [14]
Multi filozofi cred ca, ne putand fi demonstrata experimental, matematica nu poate fi o stiinta dupa definitia data de Karl Popper. [15] In anii 1930, lucrari importante de logica matematica au aratat ca matematica nu poate fi redusa la logica si Karl Popper a tras concluzia ca "cele mai multe teorii matematice sunt, ca si cele din fizica si biologie, deductive: ca urmare, matematica pura, in cele din urma, devine mult mai aproape de stiintele naturii ale caror ipoteze sunt presupuneri, asa cum s-a observat recent"[16]. Alti ganditori, printre care Imre Lakatos, au afirmat ca matematica insasi falsifica realitatea.
Un alt punct de vedere ar fi acela ca anumite domenii stiintifice (cum ar fi fizica teoretica) sunt de fapt stiinte matematice cu axiome care corespund realitatii. Cercetatorul in fizica teoretica J. M. Ziman a propus ca stiintele sa fie considerate cunostinte publice iar matematica sa fie inclusa intre ele. In orice caz, matematica are multe parti comune cu stiintele fizice, folosindu-se de studiul logic al unor ipoteze. Intuitia si experimentele au, de asemenea, roluri importante in formularea ipotezelor, atat in matematica, cat si in (alte) stiinte. Matematica experimentala continua sa capete o importanta tot mai mare intre stiintele matematice, in acest sens, computerizarea si simularea jucand roluri tot mai importante in stiinte si in matematica, slabind astfel obiectiile potrivit carora matematica nu ar utiliza metode stiintifice.
In 2002, in cartea sa, "A New Kind of Science", Stephen Wolfram sustinea ca matematica computationala merita sa fie explorata empiric, ca orice domeniu stiintific cu toate atributele. Opiniile matematicienilor in aceasta privinta sunt diferite. Multi dintre ei cred ca a denumi acest domeniu o stiinta inseamna a-i reduce importanta laturii sale estetice si a-i denatura istoria sa in cadrul celor 7 (sapte) arte libere; altii, dimpotriva, sustin ca ignorarea interferentelor cu stiintele inseamna a vedea cu un singur ochi deoarece aplicatiile matematicii in stiinte siinginerie au adus multe inovatii in matematica. Intr-un fel, aceste puncte de vedere diferite s-au transformat in dezbateri filosofice: daca matematica a fost si este creata (ca in arta) sau descoperita (ca in stiinta). A devenit un fapt obisnuit sa vezi universitati care au incluse sectii de Stiinta si Matematica, aratand in acest fel ca aceste doua domenii sunt privite ca fiind aliate dar nu identice. In practica, matematicile sunt in general grupate cu stiintele la nivele grosiere, dupa care sunt separate pe parcursul specializarii. Aceasta este una din chestiunile care fac obiectul filosofiei matematicii.
Premiile in matematica sunt in general tinute separat de echivalentele lor din stiinta. Cel mai prestigios premiu in matematica este Medalia Fields, stabilit in 1936 si acum acordat odata la 4 (patru) ani. Este adesea considerat, in mod eronat, echivalentul premiilor Nobel pentru stiinte. Premiul Wolf pentru Matematica, instituit in 1978, recunoaste realizarile pentru intreaga viata iar alt mare premiu international, Premiul Abel [17], a fost introdus in 2003. Acestea sunt acordate pentru lucrari speciale, care pot fi inovatii sau rezolvari ale unor probleme remarcabile dintr-un domeniu anume. O faimoasa lista de 23 de probleme deschise de acest fel, numita "Problemele lui Hilbert", a fost alcatuita de matematicianul german David Hilbertin 1900. Aceasta lista a devenit celebra printre matematicieni si in cele din urma noua dintre ele au fost rezolvate. O lista noua, intitulata "Problemele pentru premiul mileniului', a fost publicata in 2000. Solutionarea fiecareia dintre ele aduce un premiu de 1 milion de dolari celui care o rezolva. Numai una dintre ele (Ipoteza lui Riemann) se regaseste intre problemele lui Hilbert.

![]()
Abacul este o metoda simpla de numarare
Studiul cantitatii incepe cu numerele (mai intai cu numerele naturale si intregi) si cu operatiile artimetice. Alte proprietati ale intregilor sunt studiate de teoria numerelor, din care au aparut unele rezultate cunoscute, precum Marea teorema a lui Fermat, dar si unele teoreme inca nerezolvate: teoria numerelor prime gemene si Conjectura Goldbach.
Pe masura ce sistemul de numerotatie a avansat, numerele intregi au fost considerate un subset al numerelor rationale, care la randul sau sunt continute de multimea numerele reale. Numerele reale sunt folosite la reprezentarea functiilor continue. Mai departe avem numerele complexe, urmate de numere hipercomplexe: cuaternion, octonion, etc.
Un alt domeniu de studiu este dimensiunea multimilor, care conduce la numerele cardinale si spre un alt concept legat de infinit: numerele alef, care permit o comparatie intre multimi de dimensiune infinita.
![]()
![]()
![]()
![]()
![]()
Numar natural
Numar intreg
Numar rational
Numar real
Numar complex
Studiul spatiului a inceput cu studiul geometriei, mai exact, al geometriei euclidiene. Trigonometria combina spatiul si numerele si cuprinde cunoscuta teorema a lui Pitagora. Studiile moderne generalizeaza teoriile asupra spatiului introducand notiunea de geometrie neeuclidiana in locul celei de geometrie euclidiana. Geometria neeuclidiana ocupa un rol central inteoria relativitatii generalizate si topologie. Cantitatea si spatiul au roluri importante in geometria analitica, geometrie diferentiala si geometrie algebrica. In cadrul geometriei diferentiale apar conceptele de "fascicul de matase" ([2]fiber bundle) si calculul spatiilor topologice. Geometria algebrica descrie obiectele geometrice prin intermediul unor seturi de solutii aleecuatiilor polinomiale, combinand conceptele de cantitate, spatiu si studiul grupurilor topologice, acestea combinand notiunile de structura si spatiu. Grupurile Lie sunt folosite in studiul spatiului, structurii si schimbarii. Topologia are foarte multe ramificatii si a fost domeniul din matematica cu cea mai mare dezvoltare in secolul XX, cuprinzand faimoasa conjectura a lui Poicaré si controversata teorema a celor patru culori, a carei demonstratie, facuta doar pe calculator, nu a fost facuta inca de om.




Teorema lui Pitagora
Trigonometrie
Geometrie diferentiala
Topologie
Geometrie fractala
Subiecte legate de variatia functiilor matematice sau de variatia numerelor.




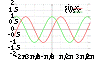
Calcul integral
Calcul vectorial
Ecuatii diferentiale
Sisteme dinamice
Teoria haosului
Multe obiecte matematice, precum multimile de numere si functiile au o structura interna. Proprietatile structurale ale acestor obiecte sunt investigate in studiul grupurilor, inelelor,campurilor si altor sisteme abstracte, care sunt la randul lor studiate de algebra abstracta. Un concept important in acest domeniu este cel de vector, generalizat in spatii vectoriale. Studiul vectorilor combina trei zone fundamentale ale matematicii: cantitatea, structura si spatiul. Algebra vectoriala dezvolta cercetarea intr-o a patra zona de cercetare fundamentala, cea a schimbarii. Un numar de probleme vechi din acest domeniu au fost rezolvate folosind teoria Galois.




Teoria numerelor
Algebra abstracta
Teoria grupurilor
Teoria ordinii
![]()

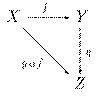
Logica matematica
Teoria multimilor
Fundamentele matematicii


![]()

Combinatorica
Computatie
Criptografie
Teoria grafurilor