|
|
|
Subiecte propuse analiza numerica
A 1. In formula de cuadratura a lui Gauss-Legendre(spre deosebire de metoda Newton-Cotes) nodurile se
aleg depinzand de functia ce urmeaza a fi integrata.
A 2. Metoda bisectiei converge liniar.
A 3. Se considera ecuatia
Dorim sa aflam o solutie
a ei pe intervalul [0,2]. Pentru a afla o astfel de solutie putem aplica metoda
bisectiei.
F 4. Daca f este un polinom de grad 4 atunci metoda lui Newton-Cotes cu 3 noduri echidistante pe [a,b]
va calcula in mod exact integrala
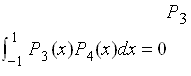A 5. Polinomul lui Legendre de grad 3 este ortogonal pe polinomul lui Legendre 
de grad 4 adica
A 6. In general metoda de interpolare a lui Lagrange e mai rapida decat metoda de interpolare cu diferente divizate.
F 7. Metoda bisectiei e intotdeauna mai rapida decat metoda lui Newton.
F 8. Polinoamul lui Legendre de grad 4 este ortogonal
pe 
adica 
F 9. In formula de cuadratura a lui Gauss-Legendre(spre deosebire de metoda Newton-Cotes) ponderile
se aleg depinzand de functia ce urmeaza a fi integrata.
A 10. Intotdeauna metoda lui Newton produce un sir de numere care converge catre solutia ecuatiei careia
ii aplicam metoda.
A 11. Se considera ecuatia f(x)=0
cu f continua pe intervalul [a,b] si f(a)f(b)<0. Atunci metoda bisectiei produce un sir ce converge catre una din solutiile ecuatiei de mai sus.
A 12. Se considera ecuatia 
Dorim sa aflam o solutie a ei pe intervalul [-1,2]. Pentru a afla o astfel de solutie putem aplica
metoda bisectiei.
A 13. Formulele Newton-Cotes sumate se obtin prin impartirea intervalului de integrare in subintervale
de lungime egala, aplicarea formulelor Newton-Cotes pe fiecare subinterval si sumarea rezultatelor obtinute.
F 14. Daca f este un polinom de grad n atunci metoda lui Newton-Cotes cu n+1 noduri echidistante pe
[a,b] va calcula in mod exact integrala
F 15. Se considera ecuatia
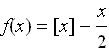
Dorim sa aflam o solutie a ei pe intervalul [-1,2]. In formula de mai sus [x] este partea intreaga a numarului x . Pentru a afla o astfel de solutie putem aplica metoda bisectiei.
16. Pentru A=
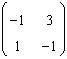sa se calculeze .
R: 4
17. Se rezolva sistemul cu matricea extinsa
Pentru rezolvarea acestui sistem putem aplica metoda GAUSS
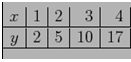18. Se da tabelul
Sa se calculeze diferenta divizata f[1,2].
R: 3 deoarece P(2)-P(1)=5-2=3
19. Se rezolva numeric ecuatia diferentiala
Fixam pasul h si consideram formula iterativa: la pasul i
unde
Aceasta este metoda RUNGE-KUTTE de ordin 4
20. Se aplica
metoda iterativa a lui Gauss-Seidel sistemului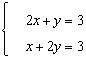 
cu predictie initiala
.
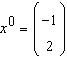Sa se calculeze urmatoarea iteratie in
metoda lui Gauss-Seidel.
R: (1/2 5/4) sau (0,50 1,25)
B
|
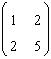pentru calculul descompunerii Cholesky A=B, unde B
este inferior triunghiulara(toate elementele deasupra diagonalei principale sunt nule). Sa se afle elementul
de pe a doua linie si prima coloana din matricea B.
R: 2
22. Se rezolva
ecuatia 
=0
pe intervalul [0,2] cu metoda bisectiei. Prima iteratie 
este
Care este a doua iteratie?
R: 0,5
23. Se rezolva cu metoda lui Gauss cu pivotare sistemul cu matricea extinsa
.
Dupa eliminari succesive se ajunge la sistemul cu matrice superior triunghiulara
R: matrice cu 2 linii si 3 coloane (2 1 3; 0 3 / 2 3 / 2)
24. Se rezolva cu metoda lui Gauss cu pivotare sistemul cu matricea extinsa
.
Dupa eliminari succesive se ajunge la sistemul cu matrice superior triunghiula
R: (3 2 1 ; 0 1 / 3 -1 / 3)
25. Se aplica metoda iterativa a lui Jacobi sistemului
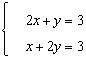cu predictie initiala
.
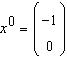Sa se calculeze urmatoarea iteratie in
metoda lui Jacobi.
R: (3 / 2 2) sau ( 1,50 2 )
26. Urmarim a aplica metoda
de integrare numerica a lui Newton-Cotes pentru a calcula 
prin utilizarea
a 2 noduri echidistante 0,2. Conform metodei Newton-Cotes
Cat este ?
R: 1
27. Se rezolva numeric ecuatia diferentiala
Notam 
.
Fixam pasul h si consideram formula iterativa
Aceasta este metoda lui Euler
28. Pentru A= sa
se calculeze 
.
R: 4
29. Pentru
A= sa se calculeze .
R: 6
30.Se considera ecuatia 
Dorim sa aflam o solutie a ei pe intervalul [0,3]. Punem a=0, b=3 apoi verificam ca f(a)f(b)<0. La primul pas
punem c=(a+b)/2 dupa care calculam f(a)f(c). Daca f(a)f(c)<0 punem b=c. Alftel
punem a=c . Acest pas este primul pas in metoda bisectiei
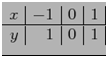31. Se da tabelul
Cat este (adica polinomul lui Lagrange corespunzator
nodului 0) ?
R: 1-x2
32. Metoda trapezului aproximeaza integrala lui f pe [a,b] dupa formula
R: (b-a)(f(b)+f(a)
33. Se rezolva cu metoda lui Gauss cu pivotare sistemul cu matricea extinsa
. Dupa eliminari succesive
se ajunge la sistemul cu matrice superior triunghiulara ..
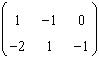
R: (-2 1 -1; 0 -1/2 -1/2)
34. Urmarim
a aplica metoda de integrare numerica a lui Newton-Cotes pentru a calcula prin
utilizarea a 3 noduri echidistante 0,1,2. Conform metodei Newton-Cotes
Cat este A0 ?
R: 0,3
35. Consideram un sistem compatibil determinat cu matrice asociata simetrica si pozitiv definita. Ce metode numerice pot fi utilizata pentru rezolvarea lui?
R: Metoda lui Cholesky (metoda radacinii patrate)
36. Aproximati integrala
cu metoda trapezului.
R: 1,5
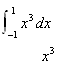37. Urmarim a aplica metoda de integrare numerica
a lui Newton-Cotes pentru a calcula prin
utilizarea a 2 noduri echidistante -1,1, si integrarea pe [-1,1] a polinomului interpolant al lui pe
nodurile -1,1. Aceasta metoda de integrare se numeste metoda trapezului
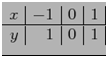38. Polinomul
lui Lagrange de ordin 2 ce interpoleaza valorile din tabelul
este x2
39. Se rezolva ecuatia 
=0
pe intervalul [0,2] cu metoda bisectiei. Prima iteratie este
1. Care este a doua iteratie?
R: 1,5
40. Aproximati
integrala
cu metoda lui Simpson.
R: 20
Metoda lui Simpson aproximeaza integrala lui f pe [a,b] cu formula (b-a)f(b)+4f(a+b)/2+f(a)) / 6
42. Aproximam integrala
cu metoda sumata a lui Simpson cu 3 subintervale. Formula de calcul este
R: f(0)=4f(1)+2f(2)+4f(30+2f(4)+4f(5)+f(6) / 3
43. Se rezolva ecuatia=
pe intervalul [0,1] cu metoda aproximatiilor succesive corespunzatoare
functiei .
Alegem predictie initiala si
notam cu 
urmatoarea iteratie si cu z solutia exacta a ecuatiei
considerate. Observam ca pe intervalul
[0,1]. Estimati eroarea 
conform teoremei de estimare a erorii in metoda
aproximatiilor succesive.
R: 3/2
44. Se rezolva numeric ecuatia diferentiala 
cu metoda lui Euler cu pas h=1. Observati ca solutia
exacta a ecuatiei este 
.
Care este aproximatia
produsa de aceasta metoda pentru 
,
unde y este solutia exacta a ecuatiei de mai sus?
R: 3
45. Pentru A=
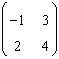sa se calculeze .
R: 7 = |-1|+|2|, |3|+|4| = max (3,7)
46. Care metode de rezolvare de sisteme liniare sunt metode iterative(adica sunt metode ce teoretic
produc un sir ce in anumite conditii converge catre solutia exacta a sistemului liniar ce se doreste a fi rezolvat)?
R: Jacob ( + Gauss- Seidel)
47. Se da tabelul
x
0
1
2
y
1
1
3
si functia
spline cubica naturala care interpoleaza datele din acest tabel.
Se specifica faptul ca pe [1,2] functia spline
e data de 
iar pe [0,1] functia spline
este data de
.
Cat este m?
R: m = -0,5
48. Se rezolva numeric ecuatia diferentiala
cu metoda lui Euler cu pas h=1. Observati ca
solutia exacta a ecuatiei este .
Care este aproximatia
produsa de aceasta metoda pentru 
?
R: 1
49. Care metode de rezolvare de sisteme liniare nu sunt metode iterative(adica sunt metode ce teoretic produc solutia exacta a sistemului liniar ce se doreste a fi rezolvat)?
R: metoda lui Gauss pentru rezolvarea de sisteme algebrice liniare ( + metoda lui Cholesky)
50. Se aplica
metoda iterativa a lui Gauss-Seidel sistemului 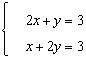cu predictie initiala
.
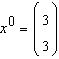Sa se calculeze urmatoarea iteratie in
metoda lui Gauss-Seidel.
R: (0 1,50)
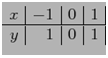51. Se da tabelul
Fie polinomul de grad 2 interpolant al valorilor
din tabel, adica .
Cat este 
?
R: 9
52. Se rezolva
ecuatia 
cu metoda lui Newton cu predictie initiala 
.
Cat este urmatoarea iteratie ?
R: 1/2
53. Se aplica
metoda iterativa a lui Jacobi sistemului 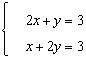cu predictie initiala
.
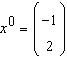Sa se calculeze urmatoarea iteratie in
metoda lui Jacobi.
R: (0,50 2)
54. Se rezolva
ecuatia 
cu metoda lui Newton cu predictie initiala .
Cat este urmatoarea iteratie ?
R: 1/4
55. Polinomul lui Lagrange de ordin 2 ce interpoleaza valorile din tabelul
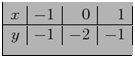
R: este x2-2
56. Aproximati integrala
cu metoda trapezului.
R: 0
57. Pentru
A=
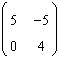sa se calculeze .
R: 10=|5|+|-5|, |0|+|4|=max (10,4)
a
si P(x) polinomul de grad 1 care interpoleaza valorile
lui f pe nodurile 0,1.
Cat este atunci P(2)?
R: 0
59. Urmarim
a aplica metoda de integrare numerica a lui Newton-Cotes pentru a calcula 
prin utilizarea a 3 noduri echidistante -1,0,1,
si integrarea pe [-1,1] a polinomului interpolant al lui 
pe nodurile -1,0,1
Aceasta metoda de integrare este exacta pe polinoame de grad mai mic sau cel mult
R: egal cu 2
60. Se rezolva numeric ecuatia diferentiala
Notam .
Fixam pasul h si consideram formula iterativa
Aceasta este metoda Euler
61. Se rezolva
sistemul cu matricea extinsa
Pentru rezolvarea acestui sistem putem aplica metoda lui Gauss
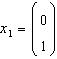
62. Se aplica metoda lui Ritz pentru calculul inversei
matricii. La primul pas se alege vector si
se calculeaza matricea 
63. Se da tabelul
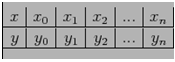
Fie polinomul lui Lagrange interpolant al valorilor din tabel, adica ,
e
grad P , calculat
cu metoda lui Lagrange. Care e cu aproximatie numarul de operatii efectuate pentru
calcularea valorii
presupunand ca 2 nu este printre valoril 
.
R: 4n2
64. Se rezolva sistemul cu matricea A data de
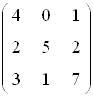
Se doreste a se aplica metoda
lui Gauss-Seidel cu predictie initiala 
De ce este metoda lui Gauss-Seidel garantata sa convearga?
R: Ca matricea sistemului este diagonal dominate pe linii
65. Se aplica metoda iterativa a lui Gauss-Seidel sistemului
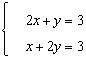cu predictie initiala
.
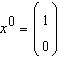S ba se calculeze urmatoarea iteratie in
metoda lui Gauss-Seidel.
R: (1,50 0,75)
66. Pentru A=
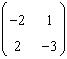sa se calculeze .
R: 5=|-2|+|1|, |2|+|-3|=max (3,5)
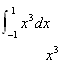67. Urmarim
a aplica metoda de integrare numerica a lui Newton-Cotes pentru a calcula prin
utilizarea a 2 noduri echidistante -1,1, si integrarea pe [-1,1] a polinomului interpolant al lui pe
nodurile -1,1. Aceasta metoda de integrare este exacta pe polinoame de grad mai mic sau egal decat
R: 1
68. Se rezolva numeric ecuatia diferentiala
Utilizam metoda Euler-Cauchy
cu h=1 . Notam 
.
Care este prima iteratie 
?
R: 3
69. Se da tabelul
Sa se calculeze diferenta divizata f[1,2,3,4,5] .
R: 0
70. Se da tabelul
x
0
1
2
y
0
2
3
si functia spline cubica naturala care interpoleaza
datele din acest tabel.
Se specifica faptul ca pe [1,2]
functia spline e data de 
iar pe [0,1]
functia spline este data de
.
Calculati valoarea lui m.
R: m=2,25
____ 71. Se da tabelul
x
0
1
2
y
1
1
4
si functia spline cubica naturala care interpoleaza
datele din acest tabel.
Se specifica faptul ca pe [1,2]
functia spline e data de 
iar pe [0,1]
functia spline este data de
.
Cat este m?
R:-0,75
72. Pentru A=
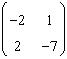sa se calculeze .
R: 5=|-2|+1, |2|+|-3|=max (3,5)
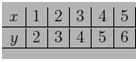73. Se da tabelul
Sa se calculeze diferenta divizata f[1,2,3,4,5] .
R: 0
74. Se rezolva numeric ecuatia diferentiala y'=y-6x, y(0)=1
cu metoda lui Euler cu
pas h=1. Notam . Cat este prima iteratie produsa
de
metoda lui Euler?
R: 2
75. Se da tabelul
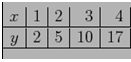
Sa se calculeze diferenta divizata f[2,3].
R: 5
B
|
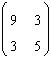pentru calculul descompunerii Cholesky A=B ,
unde
B este inferior triunghiulara(toate elementele deasupra diagonalei principale sunt nule). Sa se afle elementul
de pe a doua linie si prima coloana din matricea B.
R: 5
77. Care este
forma polinoamelor Lagrange de interpolare pe nodurile ?
R: ?
Se rezolva ecuatia 
cu metoda lui Newton cu predictie initiala .
Cat este urmatoarea iteratie ?
R: 1/4
79. Se rezolva numeric ecuatia diferentiala
y'=y+x, y(0)=1
cu metoda lui Euler cu pas
h=1. Notam .
Care este aproximatia produsa de aceasta metoda pentru y(1), unde y este solutia
exacta a ecuatiei diferentiale de mai sus?
R: 2
80. Se considera functia 
si P(x) polinomul lui Lagrange de grad 1 care interpoleaza
valorile lui f pe nodurile 0,1 . Cat este atunci P(2)?
R: 1
81. Urmarim
a aplica metoda de integrare numerica a lui Newton-Cotes pentru a calcula 
prin utilizarea a 3 noduri echidistante -1,0,1.
Conform metodei Newton-Cotes
este aproximata de
unde este un anumit polinom de grad cel mult 2. Cat
este ?
R: X
82. Urmarim
a aplica metoda de integrare numerica a lui Newton-Cotes pentru a calcula prin
utilizarea a 3 noduri echidistante -1,0,1, si
integrarea pe [-1,1] a polinomului interpolant al lui pe
nodurile -1,0,1. Aceasta metoda de integrare cu trei noduri se numeste metoda SIMPSON
R: Simpson
83. Se rezolva sistemul compatibil determinat cu matricea extinsa A data de
Se doreste a se aplica metoda
lui Jacobi cu predictie initiala .
De ce este metoda lui
Jacobi garantata sa convearga?
R: ca matricea sistemului este diagonal dominata pe linii
84. Se rezolva ecuatia 
=0
pe intervalul [0,2] cu metoda bisectiei. Prima iteratie este
1. Care este a doua iteratie?
R: 0,5
85. Se aplica metoda lui Ritz pentru calculul inversei
matricii . La primul pas se alege
vector si
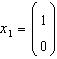
se calculeaza matricea
R: matrice 2 linii cu 2 coloane (1/2 0; 0 0)
86. Se rezolva numeric ecuatia diferentiala
, y(1)=1
utilizam metoda Euler-Cauchy
cu pas h= . Notam . Efectuam zece iteratii in metoda
Euler-
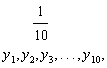Cauchy. Obtinem iteratiile succesive . Atunci 
este aproximatia produsa de metoda numerica pentru
2
87. Se considera ecuatia
Pentru rezolvarea ei vom
alege si apoi vom defini recursiv .
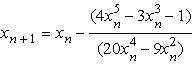
Aceasta este metoda Newton
88.Aproximam integrala
cu metoda sumata a trapezului cu 3 subintervale. Formula utilizata este ...
R: (f(0)+2f(1) +2f(2)+f(3)) / 2
89. Se considera functia si polinomul de grad
4 care interpoleaza valorile lui f pe
nodurile 1,2,3,4,5 . Cat este ?
R: 1
90. Se rezolva cu metoda lui Gauss cu pivotare sistemul cu matricea extinsa
.
Dupa eliminari succesive se ajunge la sistemul cu matrice superior triunghiulara
R: (3 1 4; 0 2/3 2/3)
91. Se aplica
metoda iterativa a lui Jacobi sistemului 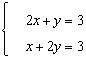cu predictie initiala
.
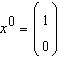Sa se calculeze urmatoarea iteratie in
metoda lui Jacobi.
R: (3/2 1) sau (1,50 1)
92. Se aplica metoda iterativa a lui Jacobi sistemului
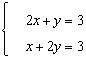cu predictie initiala
.
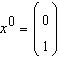Sa se calculeze urmatoarea iteratie in
metoda lui Jacobi.
R: (1 3/2) sau (1 1,50)
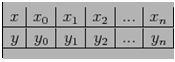93. Se da tabelul
Notam cu polinomul lui Lagrange corespunzator nodului
i adica 
are grad n s
i
daca
si . Atunci
polinomul lui Lagrange ce interpoleaza valorile din tabelul de mai sus
este dat de formula:
R: P(x) = Sni=0 yili (x)
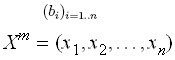94. Consideram
un sistem compatibil determinat cu matrice asociata 
si termen
liber . Consideram urmatoarea formula recursiva: la pasul m avem vectorul
si calculam urmatoarea
iteratie dupa
formula pentru i de la 1 la n
Ce metoda numerica este caracterizata de aceasta formula recursiva?
R: Jacobi (pentru rezolvarea de sisteme liniare)
95. Se aplica metoda iterativa a lui Gauss-Seidel sistemului
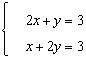cu predictie initiala
.
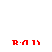
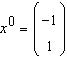Sa se calculeze urmatoarea iteratie in
metoda lui Gauss-Seidel.
96. Ce metoda de interpolare utilizeaza polinoamele
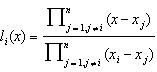
R: Metoda de interpolare cu polinoame Lagrange
97. Se rezolva
ecuatia = pe intervalul
[0,1] cu metoda aproximatiilor succesive corespunzatoare
functiei .
Alegem predictie initiala si
notam cu urmatoarea iteratie si cu z solutia exacta a ecuatiei
considerate. Observam ca pe intervalul
[0,1]. Estimati eroarea conform teoremei de estimare a erorii in metoda
aproximatiilor succesive.
R: 1/2
98. Se da tabelul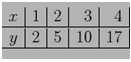
Sa se calculeze diferenta divizata f[3,4].
R: 7
99. Se aplica
metoda iterativa a lui Gauss-Seidel sistemului 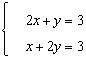cu predictie initiala
.
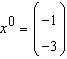Sa se calculeze urmatoarea iteratie in
metoda lui Gauss-Seidel.
R: (3 0 )
100. Se da tabelul
x
0
1
2
y
0
1
3
si functia spline cubica naturala care interpoleaza
datele din acest tabel.
Se specifica faptul ca pe [1,2]
functia spline e data de 
iar pe [0,1]
functia spline este data de
.
Cat este m?
R: m= 0,75
101. Se rezolva ecuatia =
pe intervalul [0,1] cu metoda aproximatiilor succesive corespunzatoare
functiei . Alegem predictie initiala 
.
Cat este urmatoarea iteratie conform metodei aproximatiilor succesive?
R: 2/3
B
|
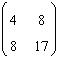pentru calculul descompunerii Cholesky A=B ,
unde B este inferior triunghiulara(toate elementele deasupra diagonalei principale sunt nule). Sa se afle
elementul de pe a doua linie si prima coloana din matricea B.
R: 4
103. Se rezolva ecuatia =
pe intervalul [0,1] cu metoda aproximatiilor succesive corespunzatoare
functiei . Alegem predictie initiala .
Cat este urmatoarea iteratie conform metodei aproximatiilor succesive?
R: 1/2
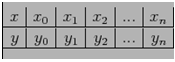104. Se da
tabelul
Notam cu polinomul de grad n ce interpoleaza valorile din tabelul de
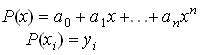mai sus adica .
Atunci coeficientii 
pot fi determinati prin rezolvarea sistemului
R: ?
105. Se rezolva numeric ecuatia diferentiala
y'=y-x, y(0)=1
cu metoda lui Euler cu pas
h=1. Notam .
Care este aproximatia produsa de aceasta metoda pentru y(1) unde y este solutia
exacta a ecuatiei diferentiale de mai sus?
R: 2
106.Se da tabelul
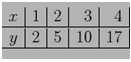
R: 1
Sa se calculeze unde este polinomul interpolant al valorilor din tabel.
107.Se rezolva ecuatia 
cu metoda lui Newton cu predictie initiala
.
Cat este urmatoarea iteratie ?
R: 1/4
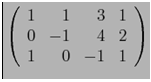108. Se rezolva sistemul cu matricea extinsa
Pentru rezolvarea acestui sistem putem aplica metoda
R: Gauss
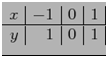109. Se da tabelul
Cat este (adica polinomul lui Lagrange corespunzator
nodului 0 din tabel evaluat la 0.5)
R: 0,75
Vrem sa aplicam formula de
cuadratura a lui Gauss-Legendre cu n noduri 
pentru aproximarea unei integrale pe intervalul
[-1,1]. Care sunt pasii efectuati in aceasta metoda de cuadratura ?
R: ?
111. Se rezolva cu metoda lui Gauss cu pivotare sistemul cu matricea extinsa
.
Dupa eliminari succesive se ajunge la sistemul cu matrice superior triunghiulara
R: (2 1 3; 0 1/2 ½ )
112. Aproximati integrala
cu metoda trapezului.
R: 0,5
B
|
|
B este inferior triunghiulara(toate elementele deasupra diagonalei principale sunt nule). Sa se afle elementul
de pe a doua linie si prima coloana din matricea B.
R: 1
114. Se rezolva
ecuatia =
pe intervalul [0,1] cu metoda aproximatiilor succesive corespunzatoare
functiei .
Alegem predictie initiala .
Cat este urmatoarea iteratie conform metodei
aproximatiilor succesive?
R: 1/2
115. Se rezolva
ecuatia =0
pe intervalul [0,2] cu metoda bisectiei. Prima iteratie este
1 iar a doua este notata 
.
Notam cu 
solutia exacta a ecuatiei ce este aproximata de
metoda bisectiei.
Estimati eroarea
|
cu teorema de estimare a erorii corespunzatoare metodei bisectiei.
R: 1/2
116. Vrem sa aplicam formula de cuadratura a lui
Gauss-Legendre cu 2 noduri 
pentru aproximarea integralei unei functii f pe
intervalul [-1,1]. Atunci in mod necesar sunt
R: radacinile polinomului de interpolare al lui Lagrange pentru functia f pe nodurile -1 si 1
Formula de cuadratura a lui Gauss-Legendre este o metoda de
R: integrare numerica
Consideram formula de cuadratura a lui Gauss-Legendre pe intervalul [-1,1] cu n noduri. Aceasta metoda este exacta pe polinoame de grad mai mic sau egal cu
R: 2n-1
Se rezolva ecuatia 
cu metoda lui Newton cu predictie initiala .
Cat este urmatoarea iteratie ?
R: 1/2
120. Se rezolva numeric ecuatia diferentiala
cu metoda lui Euler cu pas h=0.5 . Notam 
.
Formula iterativa din metoda lui Euler in acest caz este
R: yi+1=yi+ 0.5(xi+sin(yi))
121. Aproximati integrala
cu metoda lui Simpson.
R: 4
122. Se aplica metoda lui Ritz pentru calculul inversei
matricii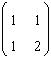 
.
La primul pas se alege vector 
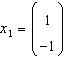
si se calculeaza matricea R: (1 -1; -1 1)
123. Se considera ecuatia
Dorim sa aflam o solutie a ei pe intervalul [0,3]. Punem a=0, b=3 apoi verificam ca f(a)f(b)<0. La
primul pas punem c=(a+b)/2 dupa care calculam f(a)f(c). Daca f(a)f(c)<0 punem b=c. Alftel punem a=c . Acest pas este primul pas in metoda
R: bisectiei
124. Se rezolva cu metoda lui Gauss cu pivotare sistemul cu matricea extinsa
.
La primul pas in aplicarea metodei lui Gauss se permuta liniile
R: 1 cu 3
125. Se rezolva sistemul cu matricea
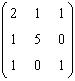
Pentru rezolvarea acestui sistem putem aplica metoda
R: metoda lui Cholessky (metoda radacinii patrate)
Ce conditii sunt suficiente pentru ca metoda lui Jacobi pentru rezolvarea de sisteme liniare sa produca un sir ce converge catre solutia exacta a sistemului liniar?
R: Matricea sistemului e diagonal dominant ape linii
127. Consideram un prim pas:
intr-o metoda numerica utilizata pentru rezolvarea unui anumit tip de sisteme liniare. Ce metoda numerica incepe cu acest pas?
R: Metoda lui Cholesky (metoda radacinii patrate)
B
|
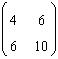pentru calculul descompunerii Cholesky A=B ,
unde B este inferior triunghiulara(toate elementele deasupra diagonalei principale sunt nule). Sa se afle
elementul de pe a doua linie si prima coloana din matricea B.
R: 3
129. Pentru A=
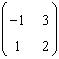sa se calculeze .
R: 5=|-1)+ |1|, |3|+|2| = max (2,5)
130. Metoda lui Simpson se incadreaza in metodele mai generale de tip
R: Newton-Cotes
131. Se da tabelul
x
0
1
2
y
1
1
2
si functia spline cubica naturala care interpoleaza
datele din acest tabel.
Se specifica faptul ca pe [1,2]
functia spline e data de 
iar pe [0,1]
functia spline este data de
.
Cat este m?
R: m= -0,25
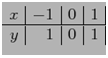132. Se da tabelul
Cat este (adica polinomul lui Lagrange corespunzator
nodului 0 din tabel evaluat la 2)
R: 3
133. Pentru A=
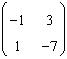sa se calculeze .
R: 8= |-1|+|3|, |1|+|-7| = max (4,8)
134. Se aplica metoda iterativa a lui Jacobi sistemului cu predictie initiala
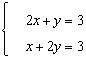
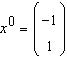
. Sa se calculeze urmatoarea
iteratie in metoda lui Jacobi.
R: (1 2)
135. Se aplica metoda lui Ritz pentru calculul inversei
matricii . La primul pas se alege
vector
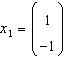
si se calculeaza matricea
R: 1/2 (1 -1; -1 1)
Metoda Newton-Cotes este o metoda de
R: integrare numerica
137. Se considera
ecuatia
Pentru rezolvarea ei vom
alege si apoi vom defini recursiv , n
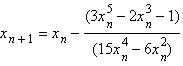
numar natural. Aceasta este metoda
R: Newton
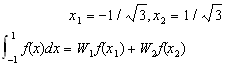138. Radacinile polinomului lui Legendre de grad 2 sunt . Se considera
urmatoarea metoda de integrare numerica:
Cum alegeti pentru
ca aceast metoda numerica sa fie exacta pe polinoame de grad cel mult 3?
R: alegem |1, |2 (L) polinoamele lui Legendre corespunzatoare nodurilor x1, x2 si apoi integram aceste
polinoame pe [-1, 1}
139. Se rezolva numeric ecuatia diferentiala y'=y, y(0)=1
cu metoda lui Euler cu
pas h=1. Notam . Calculati aproximatia
produsa de aceasta
metoda pentru y(1) unde y(x) e solutia exacta a ecuatiei de mai sus.
R: 2
B
|
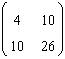pentru calculul descompunerii Cholesky A=B
unde B este inferior triunghiulara(toate elementele deasupra diagonalei principale sunt nule). Sa se afle
elementul de pe a doua linie si prima coloana din matricea B.
R: 5
141. Se rezolva numeric ecuatia diferentiala
,
y(1)=1
Utilizam metoda Euler cu h=1/20. Notam . Efectuam 20 de iteratii in metoda Euler. Obtinem
iteratiile succesive 
.Atunci 
este aproximatia produsa de metoda numerica
Pentru
R: 2
142. Se aplica
metoda lui Ritz pentru calculul inversei matricii .
La primul pas se alege vector 
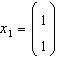si
se calculeaza matricea
R: 1/6 ( 1 1; 1 1)
143. Consideram un sistem compatibil
determinat cu matrice asociata si termen
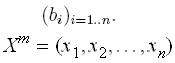liber . Consideram
urmatoarea formula recursiva: la pasul m avem vectorul
si calculam urmatoarea
iteratie
dupa formula pentru i de la
1 la n 
Ce metoda numerica este caracterizata de aceasta formula iterativa?
R: Metoda lui Cholesky (metoda radacinii patrate)
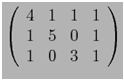144. Se rezolva
sistemul cu matricea extinsa
Pentru rezolvarea acestui sistem putem aplica metoda
R: Gauss
145. Vrem sa aplicam formula de cuadratura a lui
Gauss-Legendre cu 2 noduri pentru
aproximarea integralei unei functii f pe intervalul [-1,1]. Aceasta metoda este exacta pe polinoame
de grad mai mic sau egal ca
R: 3
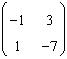
146. Pentru
A= sa se calculeze .
R: 10= |-1|+|1|, |3|+|-7| = max (2,1
