
|
|
|
Derivate partiale si diferentiale de ordin superior
Fie D un deschis din Rn si f:D![]() R o functie derivabila prtial pe D.
Fie
R o functie derivabila prtial pe D.
Fie ![]() , i=
, i=![]() cele n derivate partiale ale lui f.
cele n derivate partiale ale lui f.
Definitia11
I.Daca exista derivate partiala in a![]() (respectiv in orice a
(respectiv in orice a![]() ) in raport cu xk a
functiei
) in raport cu xk a
functiei![]() , atunci aceasta se va numi derivata partiala de ordin doi a
functiei f in punctual a(respective pe D) si se va nota prin
, atunci aceasta se va numi derivata partiala de ordin doi a
functiei f in punctual a(respective pe D) si se va nota prin
(1)![]() sau f''
sau f''![]() (a) daca i
(a) daca i![]() k
k
si
(2)![]() sau f''
sau f''![]() (a) daca i=k
(a) daca i=k
![]() cu i
cu i![]() k se vor numi derivate
mixte de ordin 2 in punctual a.
k se vor numi derivate
mixte de ordin 2 in punctual a.
II. Daca![]() este derivabila partial pe D in
raport cu variabila xk , atunci se obtin functiile
este derivabila partial pe D in
raport cu variabila xk , atunci se obtin functiile ![]() :D
:D![]() , i
, i![]() k si
k si ![]() daca i=k numite, derivate partiale de ordin 2.
(
daca i=k numite, derivate partiale de ordin 2.
(![]() cu i
cu i![]() k se va numi derivata partiala mixta de ordin 2)
k se va numi derivata partiala mixta de ordin 2)
Ex1.
Fie f:R2![]() R definita prin f(x1,x2)=sin(
R definita prin f(x1,x2)=sin(![]() ).Atunci
).Atunci
![]()
![]()
![]()
![]()
![]()
![]()
(toate derivatele partiale au fost calculate in punct curent).
Derivatele partiale de ordin superior se vor
defini in aceeasi maniera ca si derivatele partiale de ordin 2. Astfel,
derivatele partiale de ordin 3 se vor defini ca derivatele partiale de ordin 1
ale derivatelor partiale de ordin 2. Spre exemplu, prin 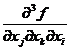 vom intelege derivate in raport cu
variabila xj a derivatei partiale de ordin doi
vom intelege derivate in raport cu
variabila xj a derivatei partiale de ordin doi ![]() .Pentru
.Pentru 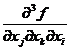 vom mai utilize si notatia f'''
vom mai utilize si notatia f'''![]()
Continuand recurrent, vom putea defini derivatele partiale de ordin q≥2 ale functiei f ca derivatele partiale de ordin 1 al ederivatelor partiale de ordin q-1.De asemenea, vom spune ca f este derivabila partial de ordin qin raport cu variabila xk daca toate derivatele partiale de ordin q-1 sunt derivabile in raport cu xk.
Derivatele partiale de ordin superior, calculate in raport cu cel putin doua variabile diferite, se numesc derivate partiale mixte.
Am definit in cap 11.2 notiunea de functie de clasa C1 pe un deschis D din Rn.In acelasi mod, vom putea defini notiunea generala de functie de clasa Cq pe D (q≥2).
Definitia2
Fie D un deschis din Rn si f:D![]() .Spunem ca f este de clasa Cq pe D (q≥2)
daca f este derivabila partial de ordin q (in raport cu toate variabilele) pe D
si toate derivatele partiale de ordin q sint continue pe D.
.Spunem ca f este de clasa Cq pe D (q≥2)
daca f este derivabila partial de ordin q (in raport cu toate variabilele) pe D
si toate derivatele partiale de ordin q sint continue pe D.
Multimea functiilor de clasa Cq (q≥2) pe D o vom nota prin Cq(D).
Daca notam prin C0(D) multimea
functiilor continue pe D, rezulta ca orice functie de clasa C1 este
si de clasa C0. In adevar, daca f![]() C1(D), atunci f este
diferentiabila conform criteriului de diferentiabilitate (vezi th 11.2.7), deci
si continua.
C1(D), atunci f este
diferentiabila conform criteriului de diferentiabilitate (vezi th 11.2.7), deci
si continua.
Tinand seama de aceasta observatie, rezulta ca orice functie de clasa Cq pe D este,in acelasi timp, si o functie de clasa Cq-1.
Definim functiile de clasa C∞ pe D (numite si functii indefinite derivabile partial pe D) drept functii de clasa Cq pe D pentru orice q=0,1,2,,,, obtinem urmatorul sir de incluziuni
C∞(D)![]()
![]() Cq(D)
Cq(D)![]() Cq-1(D)
Cq-1(D)![]()
![]() C1(D)
C1(D)![]() C0(D).
C0(D).
In exemplul 1 am vazut ca derivatele partiale
mixte de ordin 2 sunt egale doua cate doua (![]()
![]()
![]() ); remarcam,insa, ca acest lucru nu
este adevarat intotdeauna.Pentru aceasta sa analizam
); remarcam,insa, ca acest lucru nu
este adevarat intotdeauna.Pentru aceasta sa analizam
Ex2.
Fie functia
f(x,y)=
Observam direct prin calcul ca
![]() pentru
pentru ![]() (x,y)
(x,y)![]() (0,0),
(0,0),
iar![]() pentru
pentru ![]() (x,y)
(x,y) ![]() (0,0),
(0,0),
de unde ![]() iar
iar ![]() x,y
x,y![]() 0.
0.
Sa studiem derivabilitatea partiala a functiei f in (0,0).
Avem ![]()
si
![]()
Prin urmare , ![]()
Sa calculam acum derivatele mixte de ordin 2 in (0,0):
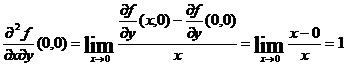
si
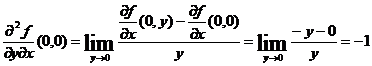
Se observa ca ![]()
In continuare , vom indica anumite cinditii suficiente care sa asigure egalitatea derivatelor partiale mixte de ordin doi intr-un punct.
Teorema1 (teorema lui Schwarz)
Fie D un deschis din Rn si f:D![]() R.Daca f are derivatele partiale
mixte
R.Daca f are derivatele partiale
mixte 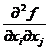 si
si 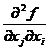 (i
(i![]() j) intr-o vecinatate a unui punct a
j) intr-o vecinatate a unui punct a![]() finite si daca functiile
finite si daca functiile 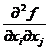 si
si 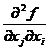 sunt continue in a, atunci
sunt continue in a, atunci
(3) 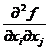 (a)=
(a)= 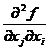 (a).
(a).
Dem.
EtapaI. Vom demonstra , mai intai, teorema entru n=2.In acest caz vom consudera f de variabile x si y in loc de x1,x2.
Fie a=(a1,a2)![]() si fie V=S(a,r) o vecinatate a lui a
pe care exista functiile
si fie V=S(a,r) o vecinatate a lui a
pe care exista functiile ![]()
![]() . Daca (x,y) este un punct arbitrar
din V a.i. x
. Daca (x,y) este un punct arbitrar
din V a.i. x![]() a1 si y
a1 si y![]() a2 sa consideram
urmatoarea expresie:
a2 sa consideram
urmatoarea expresie:
(4)E(x,y)=f(x,y)-f(a1,y)-f(x, a2)+f (a1, a2).
Observam ca exista un interval deschis I![]() R ce contine pe a1 a.i.
pentru orice u
R ce contine pe a1 a.i.
pentru orice u![]() punctele (u,y) si (u,a2)
apartin lui V.
punctele (u,y) si (u,a2)
apartin lui V.
Definim functia
(5) ![]() =f(u,y)-f(u,a2), pentru
=f(u,y)-f(u,a2), pentru ![]() u
u![]() I.
I.
Desen
Atunci E(x,y)= ![]()
![]()
Cum f este derivabila partial in raport cu x pe V
rezulta ca ![]() satisface conditiile teoremei lui
Lagrange pe intervalul [x,a1] (sau [a1,x]).Atunci ,
exista un punct
satisface conditiile teoremei lui
Lagrange pe intervalul [x,a1] (sau [a1,x]).Atunci ,
exista un punct ![]()
![]() (x,a1) (sau
(x,a1) (sau ![]() (a1,x)) a.i.
(a1,x)) a.i.
(6)
E(x,y)= ![]()
![]() =(x-a1)
=(x-a1) ![]() '(
'(![]() ).
).
Dar
din (5) ![]() '(
'(![]() )=
)=![]() , care inlocuita in
relatia (6) da
, care inlocuita in
relatia (6) da
(7)
E(x,y)=(x-a1)[ ![]() ].
].
(8) Observam, acum , ca functia ![]() , definite pe un interval deschis J
, definite pe un interval deschis J![]() R astfel ales incat a2
R astfel ales incat a2![]() si pentru orice v
si pentru orice v![]() J punctual (
J punctual (![]()
![]() V, satisface si ea conditiile
teoremei lui Lagrange pe intervalul [y,a2](sau [a2,y])
intrucat exista
V, satisface si ea conditiile
teoremei lui Lagrange pe intervalul [y,a2](sau [a2,y])
intrucat exista ![]() pe V.
pe V.
Si atunci , din (7) obtinem
(8)
E(x,y)= (x-a1)[ ![]()
![]() ]=(x-a1)(y-a2)
]=(x-a1)(y-a2)![]()
=(x-a1)(y-a2)
![]()
![]()
Unde ![]() (sau (a2,y))
(sau (a2,y))
Inversand rolurile celor doua variabile x,y si
facand un rationament complet analog, vom gasi un punct ![]()
![]() (x,a1) ( sau
(x,a1) ( sau ![]()
![]() (a1,x)) si un punct
(a1,x)) si un punct ![]()
![]() (y,a2) ( sau
(y,a2) ( sau ![]()
![]() (a2,y)) a.i.
(a2,y)) a.i.
(9) E(x,y)=( x-a1)( y-a2) ![]()
![]()
![]()
Din relatia (8) si (9) gasim
(10) ![]()
![]()
![]()
![]()
![]()
Fie acum, un sir de puncte (xn,yn)![]() V a.i. (xn,yn)
V a.i. (xn,yn)![]() (a1,a2) cu xn
(a1,a2) cu xn![]() a1 si yn
a1 si yn![]() a2 .
a2 .
Din consideratiile de mai sus, vom obtine
punctele ![]() din intervalul (xn,a1)
(sau (a1,xn)) si punctele
din intervalul (xn,a1)
(sau (a1,xn)) si punctele ![]() din intervalul (yn,a2)
(sau (a2,yn)) pentru
din intervalul (yn,a2)
(sau (a2,yn)) pentru ![]() n
n![]() a.i. sa aiba loc
a.i. sa aiba loc
(10') ![]()
![]()
![]()
![]()
![]()
![]() n
n![]()
Cum (xn,yn)![]() (a1,a2),
rezulta ca
(a1,a2),
rezulta ca ![]()
![]()
![]()
![]()
![]() si deci
si deci
![]()
![]()
![]() ( a1,a2), (
( a1,a2), (![]()
![]()
![]() (a1,a2).
(a1,a2).
Facand n![]() in (10') si tinand seama de
continuitatea in a a functiilor
in (10') si tinand seama de
continuitatea in a a functiilor ![]() si
si ![]() , obtinem
, obtinem ![]() (a1,a2)=
(a1,a2)= ![]() (a1,a2).
(a1,a2).
Etapa a-II-a.
Daca n>2, fara a micsora generalitatea,
putem presupune ca i<j.Fie a=(a1,a2,..,an)![]() si fie functia
si fie functia
g(x,y)=f(a1,.,ai-1,x,ai+1,.,aj-1,y,aj+1,.,an), definite pe un deschis ce contine punctual (ai,aj).Aplicand rezultatul obtinut in etapa I functiei g, avem
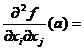
![]()
![]()
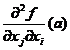 , cu care teorema este complet
demonstrate.
, cu care teorema este complet
demonstrate.
Corolar1
Fie D un deschis din Rn si fie f:D![]() Daca f este de clasa C1 pe D si derivatele partiale
Daca f este de clasa C1 pe D si derivatele partiale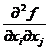 si
si 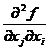 (i
(i![]() j) exista si sunt continue pe D,
atunci
j) exista si sunt continue pe D,
atunci
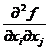
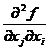
Corolar2
Daca f ![]() Cq(D), atunci derivatele
partiale mixte de ordin ≤q nu depend de ordinea de derivare.
Cq(D), atunci derivatele
partiale mixte de ordin ≤q nu depend de ordinea de derivare.
Teorema2 (Criteriul lui Young)
Fie D un deschis din Rn si f:D![]() .Daca f este derivabila partial pe o
vecinatate V a punctului a
.Daca f este derivabila partial pe o
vecinatate V a punctului a ![]() iar derivatele partiale
iar derivatele partiale ![]() i=
i=![]() , sunt diferentiabile in punctul a, atunci exista derivatele partiale
mixte de ordinal doi si sunt egale in a.
, sunt diferentiabile in punctul a, atunci exista derivatele partiale
mixte de ordinal doi si sunt egale in a.
Dem.
La fel ca in demonstratia criteriului lui Schwarz
putem reduce consideratiile la cazul n=2.De asemenea, vom lua a=(a1,a2), (x,y)
un punct arbitrar din V cu x![]() a1, y
a1, y![]() a2 si E(x,y) ca in (4).
Utilizand aceeasi functie auxiliara
a2 si E(x,y) ca in (4).
Utilizand aceeasi functie auxiliara ![]() si repetand rationamentul facut in
demonstratia criteriului lui Schwarz, rezulta ca exista
si repetand rationamentul facut in
demonstratia criteriului lui Schwarz, rezulta ca exista ![]() (x,a1) (sau (a1,x))
astfel ca sa aiba loc
(x,a1) (sau (a1,x))
astfel ca sa aiba loc
(7)
E(x,y)=( x-a1)[![]()
Adunand si scazand in paranteza ![]() (a1,a2), avem
(a1,a2), avem
(11)E(x,y)= (x-a1) [![]()
Intrucat ![]() este diferentiabila in punctul (a1,a2),rezulta
ca exista o functie
este diferentiabila in punctul (a1,a2),rezulta
ca exista o functie ![]() a.i.
a.i. ![]() iar
iar
(12) ![]()
![]() pentru
pentru ![]()
![]()
![]()
Utilizand aceasta relatie in (11), obtinem
E(x,y)=
=(x-a1)[(![]()
![]() (a1,a2)+(y-a2)
(a1,a2)+(y-a2)
![]()
![]()
![]()
![]()
![]() (y-
(y-![]()
![]()
![]()
(x-a1)[(y-![]()
![]()
![]()
![]()
![]()
Pe de alta parte , si ![]() este o funtie diferentiabila pe V si
atunci exista o functie
este o funtie diferentiabila pe V si
atunci exista o functie ![]() a.i.
a.i. ![]() , iar
, iar
(14) ![]()
![]()
![]()
![]()
![]()
Inversand rolurile celor doua variabile x si y tinand seama de (14), vom obtine
(15) E(x,y)= (y-a2)[(x-a1)![]()
![]()
![]()
![]()
unde ![]() (y,a2) ( sau (a2,y)).
(y,a2) ( sau (a2,y)).
Din (13) si (15) obtinem
(x-a1)[(y-![]()
![]() +(x-a1)
+(x-a1) ![]()
![]()
![]() (x-a1)=
(x-a1)=
(x-a1)[(y-![]()
![]() + (y-
+ (y-![]()
![]()
![]()
![]() ((y-
((y-![]()
Impartind prin (x-a1)(y-![]() ) ambii membrii ai ultimei egalitati
avem:
) ambii membrii ai ultimei egalitati
avem:
(16)![]()
![]()
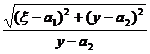
![]()
![]()
![]()
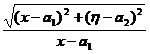
![]()
Luand , acum, un sir (xn,yn)![]() (a1,a2), cu xn
(a1,a2), cu xn![]() a1, yn
a1, yn![]() a2 a.i. |xn-a1|=|yn-a2|,
rezulta ca pentru orice n
a2 a.i. |xn-a1|=|yn-a2|,
rezulta ca pentru orice n![]() exista un
exista un ![]() (sau (a1,xn))si un
(sau (a1,xn))si un ![]() (sau (a2,yn))
a.i. sa aiba loc (16) , adica
(sau (a2,yn))
a.i. sa aiba loc (16) , adica
(16') ![]()
![]()
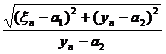
![]()
![]()
![]()
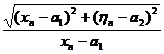
![]()
Facand n![]() in (16') si tinand seama ca
in (16') si tinand seama ca ![]()
![]() , iar
, iar
![]() | ≤1, |
| ≤1, |![]() |≤1, rezulta ca
|≤1, rezulta ca ![]()
![]() , adica tocmai ceea ce trebuia
demonstrat.
, adica tocmai ceea ce trebuia
demonstrat.
Corolar3
Fie D un
deschis din Rn si f:D![]() .Daca f este derivbila partial pe D
(in raport cu toate variabilele), iar functiile
.Daca f este derivbila partial pe D
(in raport cu toate variabilele), iar functiile ![]() , i=
, i=![]() , sunt diferentiabile pe D, atunci
exista toate derivatele partiale de ordinal doi iar cele mixte sunt egale doua
cate doua pe D.
, sunt diferentiabile pe D, atunci
exista toate derivatele partiale de ordinal doi iar cele mixte sunt egale doua
cate doua pe D.
Observatii!
1. Se observa ca daca D este un deschis din Rn, f:D![]() admite derivate partiale de ordin
doi pe o vecinatate V a unui punct a
admite derivate partiale de ordin
doi pe o vecinatate V a unui punct a![]() care sunt continue in a, atunci derivatele partiale de ordin
1,
care sunt continue in a, atunci derivatele partiale de ordin
1, ![]() , i=
, i=![]() , avand derivate partiale de ordin 1
continue in a, sunt functii
diferentiabile in a si atunci,
conform criteriului lui Young, derivatele partiale mixte de ordin 2 sunt egale
doua cate doua in punctul a.
, avand derivate partiale de ordin 1
continue in a, sunt functii
diferentiabile in a si atunci,
conform criteriului lui Young, derivatele partiale mixte de ordin 2 sunt egale
doua cate doua in punctul a.
2. Criteriile lui Schwarz si Young au campuri de aplicabilitate diferite, ambele asigurand egalitatea deriavtelor mixte.Se observa, insa , ca pentru functii de clasa C2 pe deschisul D sunt aplicabile ambele criterii.
Definitia3
Fie f:D![]() , unde D este un deschis din Rn.
, unde D este un deschis din Rn.
I. Spunem ca f este de q (q≥2) ori diferentiabila intr-un punct a![]() daca f este de q-1 ori diferentiabila
partial intr-o vecinatate V a lui a,
iar toate derivatele partiale de ordin q-1 ale lui f sunt diferentiabile in a.
daca f este de q-1 ori diferentiabila
partial intr-o vecinatate V a lui a,
iar toate derivatele partiale de ordin q-1 ale lui f sunt diferentiabile in a.
II. Spunem ca f este de q ori diferentiabila pe D daca este de q ori diferentiabila in orice
punct a![]()
Observatie!
Din criteriul lui Young rezulta ca daca f este
diferentiabila de q ori in punctul a![]() atunci exista toate derivatele
partiale de ordin q in punctual a iar derivatele partiale mixte de ordin ≤
q nudepind de ordinea de derivare.
atunci exista toate derivatele
partiale de ordin q in punctual a iar derivatele partiale mixte de ordin ≤
q nudepind de ordinea de derivare.
Propozitia1
Daca f:D![]() , unde D este un deschis din Rn
, este derivabiola partial de ordin q pe D si daca derivatele partiale de ordin
q sunt continue in a, atunci f este
diferentiabila de ordin q in punctul a.
, unde D este un deschis din Rn
, este derivabiola partial de ordin q pe D si daca derivatele partiale de ordin
q sunt continue in a, atunci f este
diferentiabila de ordin q in punctul a.
Dem.
Intrucat f este derivabila partial de ordin q in punctul a,rezulta ca exista derivatele partiale de ordin q-1 pe o vecinatate V a lui a.In plus, aceste derivate partiale rivate partiale pe V, care sunt continue in a, ceea ce asigura ca derivatele partiale de ordin q-1 sunt diferentiabile in a. Conform definitiei 3, f este de q ori diferentiabila in punctul a.
Am vazut in cap 11.2 ca pentru o functie f diferentiabila intr-un punct a are loc egalitatea
f(a)(h)=h1![]() h2
h2![]() .+hn
.+hn![]() ,
, ![]() h=(h1,h2,.,hn)
h=(h1,h2,.,hn)![]() Rn
Rn
Tinand seama de definitia diferentiabilitatii de ordin q intr-un punct, este naturat sa consideram urmatoarea definitie a diferentialei de ordin q a unei functii intr-un punct:
Definitia4
Fie f:D![]() , unde D este un deschis din Rn
, o functie de q ori diferentiabila intr-un punct a
, unde D este un deschis din Rn
, o functie de q ori diferentiabila intr-un punct a![]() Numim diferentiala de ordin q a functiei f in punctul a functia dqf(a):Rn
Numim diferentiala de ordin q a functiei f in punctul a functia dqf(a):Rn![]() R definite prin
R definite prin
(17) dqf(a)(h)=(
h1![]() h2
h2![]() .+hn
.+hn![]() )(q) ,
)(q) , ![]() Rn, unde notatia din membrul
al doilea inseamna ca expresia din paranteza se ridica, formal, la puterea simbolica q dupa o formula clasica de tip
"binomila" in care puterea semnfica ordinal de derivare.
Rn, unde notatia din membrul
al doilea inseamna ca expresia din paranteza se ridica, formal, la puterea simbolica q dupa o formula clasica de tip
"binomila" in care puterea semnfica ordinal de derivare.
Astfel
(![]() ) (q) reprezinta
) (q) reprezinta ![]()
![]() )(q-1)(
)(q-1)( ![]() ) reprezinta
) reprezinta 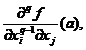
![]() )(q-1)(
)(q-1)( ![]() )(2) reprezinta
)(2) reprezinta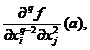 etc...,
etc...,
sau, in general,
(![]()
![]()
![]()
![]()
![]()
![]() reprezinta
reprezinta ![]()
Unde ![]()
![]()
![]()
Observatii!
1. In formula (17) derivatele partiale mixte de ordin ≤ q sunt egale in baza corolarului3.
2.
In cazul q=2 , d2f(a) este o forma patratica d2f(a)(h)=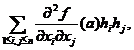
![]() Rn.
Rn.
Matricea asociata acestei forme patratice , adica
H=[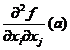 ]1≤i,j≤n se numeste matricea hessiana a lui f in a
si, conform observatiei1, este o matrice simetrica.
]1≤i,j≤n se numeste matricea hessiana a lui f in a
si, conform observatiei1, este o matrice simetrica.
3.
In cazul q=3, d3f(a)(h)= 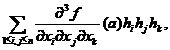
![]() Rn.
Rn.
4. Formula (17) se mai poate scrie si sub forma
(17') dqf(a)(h)=[![]() ](q),
](q), ![]() Rn,
Rn,
Sau , punand hk=prkhd(prkh)=dxk(a), sub forma
(17'') dqf(a)(h)=[![]() ](q),
](q),![]() Rn.
Rn.
Daca (17'') are loc pentru ![]() Rn si
Rn si ![]() , atunci o putem scrie si sub forma
condensata
, atunci o putem scrie si sub forma
condensata
(18)
dqf=[![]() ](q).
](q).
5. Pentru n=2, daca f:D![]() , unde D este un deschis din R2,
formula (17) devine
, unde D este un deschis din R2,
formula (17) devine
(19) dqf(a)(h)=(
h1![]() h2
h2![]() )(q),
)(q), ![]() R2,
R2,
formula (17'') devine
(20) dqf(a)(h)=(![]() )(q) ,
)(q) ,
iar (18) devine
(21)dqf=(![]() )(q) .
)(q) .
Ex2.
Sa se scrie diferetialele de ordin 1 si 2 in
punct current pentru functia f:R3![]() R definita prin
R definita prin
f(x,y,z)=cos(x+2y+3z).
Sa calculam , mai intai, derivatele partiale de ordin1. Avem
![]()
![]() si
si
![]() de unde
de unde
df=-sin(x+2y+3z)dx-2sin(x+2y+3z)dy-3sin(x+2y+3z)dz.
Sa
determinam diferentiala de ordin 1 in punctual a=(![]() ).
).
Avem df(a)=-sin![]()
![]()
Pentru a determina d2f sa calculam derivatele partiale de ordin 2. Obtinem
![]()
![]()
![]()
![]()
![]()
![]()
Atunci
d2f=-cos(x+2y+3z)(dx2+4dy2+9dz2+4dxdy+6dxdz+12dydz).
Teorema3 (Formula lui Taylor)
Fie D un
deschis din Rn, f:D![]() R o functie de q+1 ori diferentiabila
pe D, a un punct din D si S(a,r) o sfera deschisa inclusa in D.Atunci, pentru orice x
R o functie de q+1 ori diferentiabila
pe D, a un punct din D si S(a,r) o sfera deschisa inclusa in D.Atunci, pentru orice x![]() S(a,r) exista un punct
S(a,r) exista un punct ![]() apartinand segmentului determinat de punctele a si x (
apartinand segmentului determinat de punctele a si x (![]() [a,x]) a.i.
[a,x]) a.i.
(22) f(x)=f(a)+![]()
Dem.
Fie v=(v1,v2,.,vn)
un versor din Rn. Daca t![]() , atunci x=a+tv
, atunci x=a+tv![]() S(a,r)
S(a,r)![]()
Sa consideram functia
(23) ![]() f(a+tv)=f(a1+tv1,a2+tv2,..,an+tvn),
f(a+tv)=f(a1+tv1,a2+tv2,..,an+tvn),
![]()
Intrucat f este de (q+1) ori diferentiabila
rezulta ca si ![]() este de (q+1) ori diferentiabila pe (-r,r).
este de (q+1) ori diferentiabila pe (-r,r).
Sa calculam cele q+1 derivate ale lui ![]() .Observam ca
.Observam ca
![]() v1
v1![]() v2
v2![]() .+vn
.+vn![]()
![]()
apoi
![]()
![]()
=[![]() ](2)=
](2)=![]()
![]() ](2).
](2).
Procedand inductive obtinem
(24) ![]()
![]() ](k) pentru k=1,2,.,q+1.
](k) pentru k=1,2,.,q+1.
Sa aplicam
formula lui Maclurin cu restul lui Lagrange functiei ![]() Obtinem pentru
Obtinem pentru
![]() exista un
exista un ![]()
![]() (sau
(sau ![]()
![]() (t,0)) a.i.
(t,0)) a.i.
(25)![]() .
.
Tinand
seama ca x=a+tv ![]() x-a=tv, din (24) avem
x-a=tv, din (24) avem
t![]()
=(x1-a1)![]()
=df(a)(x-a)
t2![]()
![]()
=[(x1-a1)
![]() ](2)=d2f(a)(x-a)
](2)=d2f(a)(x-a)
tq![]() dqf(a)(x-a)
dqf(a)(x-a)
si
tq+1![]() = tq+1[
= tq+1[![]() ](q+1)=
](q+1)=
=[![]() ](q+!)=
](q+!)=
=[(x1-a1) ![]() ](q+1)=
](q+1)=
=dq+1f(![]() )(x-a),
)(x-a),
unde
![]() a+
a+![]() v
v![]() [a,x], care, inlocuite in (25), conduc la
[a,x], care, inlocuite in (25), conduc la
f(x)=f(a)+![]()
adica
tocmai relatia (22) ce trebuia demonstrate (![]() si
si ![]()
In particular, obtinem
Teorema4
Daca D este un deschis din R2, f:D![]() o functie de doua ori diferentiabila
pe D, si a=(a1,a2)
o functie de doua ori diferentiabila
pe D, si a=(a1,a2)![]() atunci exista un r>0 a.i. pentru
orice punct (x,y)
atunci exista un r>0 a.i. pentru
orice punct (x,y)![]() S(a,r)
S(a,r)![]() D are loc relatia
D are loc relatia
(22') f(x,y)=f(a1,a2)+ ), unde
), unde ![]() este un punct situate pe segmentul ce uneste
punctele (a1,a2) si (x,y).
este un punct situate pe segmentul ce uneste
punctele (a1,a2) si (x,y).