Componentele modelului cantitativ, Structura modelelor cantitative

SLIDE 5

Agenda

1. Faza de proiectare
2. Componentele modelului cantitativ
3. Structura modelelor cantitative

1. Faza de proiectare

Gasirea, dezvoltarea & analizarea posibilelor actiuni de desfasurat → include intelegerea problemei & testarea fezabilitatii solutiilor + construirea, testarea & validarea modelului de luare a deciziilor.

Modelarea = abstractizarea problemei in forme cantitative &/ calitative. Pentru modele matematice - identificarea variabilelor & stabilirea relatiilor dintre ele, eventual simplificarea ipotezelor. Exemplu, relatiile dintre 2 variabile se presupun liniare, chiar daca ele au un efect neliniar → gasirea unui echilibru intre simplificare & reprezentarea realitatii: o simplificare duce la costuri mai mici in rezolvare & solutii mai rapide dar poate denatura realitatea.

Modelarea = arta + stiinta:

• ca stiinta - clase de modele standard disponibile - determinarea modelului aplicabil in situatia data;
• ca arta - creativitatea & finetea in determinarea simplificarilor ipotezelor, combinarea caracteristicilor claselor de modele, modul de integrare a modelelor pentru a obtine solutii corecte.

Subiecte referitoare la modelele cantitative (matematice, financiare, etc.):

componentele modelului;

structura modelului;

selectarea unui principiu de alegere (criteriu pentru evaluare);

generarea alternativelor;

previzionarea iesirilor;

masurarea iesirilor;

scenarii.

2. Componentele modelului cantitativ

Orice model - 3 componente de baza:

variabilele decizionale

variabilele necontrolabile (parametrii);

variabilele de iesire (rezultatele)

legate prin relatii matematice. In modelele necantitative - relatiile simbolice / calitative.

Rezultatele deciziilor - determinate de:

• decizia luata (valoarea variabilelor de decizie);
• factorii care nu pot fi controlati de decident (de exemplu mediul);
• relatiile dintre variabile.

Exemplu de variabile din modele economice din slide trecut:

2.1.          Variabilele rezultat

Nivelul de efectivitate a sistemului - cat de bine functioneaza sistemul pentru a obtine scopul (rezultatul dorit) - reprezinta iesiri / variabile dependente. Evenimentul descris de variabilele de iesire presupune ca in prealabil au avut loc alte evenimente → sunt rezultatul unor valori ale variabilelor decizionale & a parametrilor.

2.2.          Variabilele decizionale

Descriu cursuri alternative ale actiunii. Nivelul acestor variabile se stabileste de decident. Exemplu, in problema de investitii, valoarea investitiei este o variabila decizionala, in probleme de planificare variabilele decizionale sunt legate de personal, timp si planificari, alte exemple sunt in tabel.

2.3.          Variabile incontrolabile / parametrii

In situatiile decizionale - factori care afecteaza variabilele de iesire dar nu sunt sub controlul decidentului. Ei pot fi ficsi = parametrii / pot lua diferite valori (variabile). Exemple: reglementari referitoare la taxe & impozite, ce si cat se cere, etc. (Tabel). Acesti factori sunt incontrolabili deoarece sunt determinati de mediu. Unii dintre acestia limiteaza actiunile decidentului → restrictii / constrangeri ale problemei.

2.4.          Variabile cu rezultate intermediare

= iesiri intermediare. Exemplu: in planificarea activitatilor pe masini, rebuturile reprezinta un rezultat intermediar, profitul total este rezultatul final, dar este influentat de rebuturi. Alt exemplu: nivelul de salarizare a angajatilor = variabila decizionala → satisfactia salariatilor (rezultat intermediar) → nivelul de productivitate (rezultat final).

3.       Structura modelelor cantitative

Componentele modelelor cantitative - legate prin relatii matematice (algebrice - ecuatii & inecuatii).

Exemplu: P=V-C - P=profit, V=venit, C=cheltueli - ecuatia descrie relatia dintre variabile.

Alt exemplu: valoarea actualizata a cash-flow:

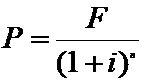
P=valoarea actuala, F = valoarea in viitor, i = rata de amortizare (procente).

Exemple mai complexe: mixul de productie. Companie de calculatoare produce 2 tipuri de calculatoare:

• CC-7 - 300 zile munca & 10.000 u.m. materiale;
• CC-8 - 500 zile munca & 15.000 u.m. materiale.

Profitul adus de CC-7 = 8.000 u.m. de CC-8 - 12.000 u.m. Fabrica are capacitate de 200.000 zile munca & buget 8.000.000 u.m. Marketingul cere cel putin 100 bucati CC-7 & 200 bucati CC-8 pe luna. Problema este: cate CC-7 & CC-8 sa se produca pe luna pentru un profit maxim.

Modelarea - standard prin programare liniara cu cele 3 componente:

• Variabile decizionale:

X₁ = nr. de unitati CC-7 de produs;

X₂ = nr. de unitati CC-8 de produs;

• Variabile rezultat:

Profit total = Z - functia obiectiv de maximizat: Z=8000X₁+12000 X₂

• Variabile necontrolate (restrictii)

Restrictii de munca:   300X₁+500 X₂ 200000 (zile)

Restrictii de buget: 10000X₁+15000 X₂ 8000000 (u.m.)

Cereri de marketing: X₁ 100 (unitati)

Cereri de marketing: X₂ 200 (unitati)

• In programarea liniara exista variabile intermediare nespecificate explicit. Modelul mai are 4 variabile intermediare si anume:
• primele doua restrictii au nevoie de doua variabile intermediare pentru a mari membrul stang pentru a deveni egal cu cel drept;
• ultimele doua restrictii au nevoie de doua variabile intermediare pentru a micsora membrul stang pentru a deveni egal cu cel drept.

Variabilele intermediare sunt importante pentru decident deoarece metodele de rezolvare a problemelor de programare liniara le stabilesc ca parametrii a senzitivitatii pentru analize de tip what-if.

Problema mixului de productie are un numar nelimitat de solutii, in ipoteza ca planul de productie global nu este limitat. Se doreste insa solutia care maximizeaza profitul.

Problema poate fi rezolvata prin metoda simplex sau utilizand add-in Solver din Excel→Tools. Solutia data cu Solver:

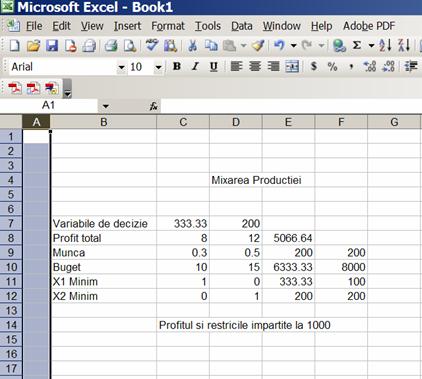
→ X₁=333.33, X₂=200, Profitul=5.066.640 u.m. Solverul mai poate da o serie de rapoarte auxiliare.

Alte probleme de optimizare:

• probleme de alocare (cea mai buna potrivire);
• programare dinamica;
• investitie (maximizarea profitului, ratei de revenire);
• programare liniara & in numere intregi;
• probleme de grafe & retele (pentru planificare);
• programare neliniara;
• modele simple de stocuri;
• modele de transport;
• modele de fire de asteptare, etc.

Evaluarea alternativelor depinde de criteriul ales, daca se cauta solutia optimala, una suboptimala sau una suficient de buna.

4.       Selectarea principiului de alegere

Principiul de alegere = criteriul ce descrie acceptabilitatea solutiei. Exista 2 principii: normativ & descriptiv.

Modelele normative

→ demonstrabilitatea faptul ca se alege cea mai buna solutie dintre toate solutiile posibile. Procesul se numeste optimizare & se atinge prin 3 metode:

• atingerea unui nivel maxim a scopului avand un set de resurse - exemplu, profit maxim la investirea unei sume de bani;
• atingerea unei rate maximale corespunzatoare unui cost (profit pe u.m. investita) sau a productivitatii;
• determinarea alternativei cu cost minim (sau alte resurse) pentru atingerea unui nivel acceptabil al scopului, exemplu: realizarea unui produs dupa o anumita specificare; care metoda va duce la realizarea lui cu costul minimal?

Teoria deciziilor normative se bazeaza pe urmatoarele ipoteze ale decidentului rational:

• omul econom - interesul sa-si maximizeze tinta; daca decidentul este rational. [Mai mult dintr-un lucru bun (venit, bucurie) este preferabil decat putin; putin dintr-un lucru rau (cost, tristete) este preferabil la mai mult].
• pentru o situatie decizionala sunt cunoscute desfasurarile actiunilor alternative & consecintele acestora / probabilitatea & valorile consecintelor sunt cunoscute;
• decidentul are o ordine a preferintelor care-i permite ordonarea consecintelor analizei.

Pot exista anomalii majore in comportamentul economic & financiar cauzate motive ca: incompetenta, lipsa de cunostinte, scopuri multiple inadecvate, neintelegerea problemei de catre decident, impactului presiunii timpului etc.

Suboptimizare

Optimizarea - decidentul ia in considerare impactul fiecarei alternative pe intreaga organizatie deoarece o decizie intr-un domeniu poate avea implicatii semnificative in alte domenii. Exemplu, departamentul de productie  dezvolta un plan de sine statator de a produce o cantitate mare dintr-un produs → costuri scazute, dar are implicatii la stocuri & marketing.

Sistemic trebuie stabilit impactul tuturor deciziilor pentru intregul sistem. → o analiza costisitoare, consumatoare de timp si complicata. In MSS se divide sistemul parti delimitate, de exemplu se ia in considerare numai o parte a organizatiei (departamentul de productie) si se incorporeaza relatiile intr-un model care amana interactiunile complexe cu celelalte componente. Aceasta abordare este o suboptimizare.

O decizie suboptimala pentru o parte a organizatiei fara a lua in considerare restul → un rezultat inferior fata de optimizarea problemei din punctul de vedere al organizatiei. Metoda - foarte practica ca fiind prima abordare in multe probleme. Scuteste de amanunte. Se analizeaza o portiune a sistemului se stabileste o solutie & se testeaza efectele asupra restului sistemului. Daca solutia nu are efecte negative semnificative se implementeaza.

Suboptimizarea se poate utiliza & pentru simplificarea ipotezelor unei probleme. De multe ori sunt detalii sau date de incorporat intr-o situatie decizionala, dar nu toate se utilizeaza in model. Daca solutia modelului pare rezonabila se considera ca fiind valida pentru problema & se adopta. Exemplu, stocurile pentru departamentul de productie de regula se impart in categoriile A/B/C. Entitatile din categoria A sunt ansambluri costisitoare, din care se comanda putine si au un nivel de stoc scazut; cele de nivel C sunt piese in general foarte ieftine (suruburi, piulite etc.) din care se comanda cantitati mari. Fiecare piesa din categoria A este monitorizata atent de management iar aprovizionarea se face cu mare grija; cele de nivel C se aprovizioneaza pe loturi anuale sau semestriale. Cele de tip B fiind intre cele doua se aprovizioneaza mai ritmic si se inventariaza periodic → suboptimizarea aprovizionarii se refera in primul rand la A.

Suboptimizarea poate marginii cautarea optimului (printr-o euristica) prin considerarea mai unui numar mai mic de criterii sau alternative eliminand o buna poarte din problema evaluarii.

Se aplica foarte bine in dezvoltarea iterativa (pas-cu-pas) a abordarii prin DSS.

Modele descriptive

Descriu lucrurile cum sunt sau cum se crede ca sunt. Se bazeaza pe instrumente matematice & se utilizeaza intensiv in DSS pentru a investiga consecintele diferitelor alternative in cazul diverselor intrari si moduri de procesare. Analizeaza performantele sistemului numai in anumite alternative & nu in toate alternativele posibile → nu garanteaza optimalitatea solutiei. Metoda de modelare cea mai uzuala din aceasta categorie este simularea. Ea a fost aplicata in multe probleme decizionale dar si in alte domenii ca jocuri pe calculator sau video. Realitatea virtuala este o forma de simulare. Mediul este unul simulat, nu unul real.

Exemplu, Metoda Monte Carlo:

MC - metoda experimentarilor statistice - metoda modelarii variabilelor aleatoare - scopul determinarea caracteristicilor repartitiilor lor.

1949 Metropolis & Ulam "The MC Method", J Amer. Stat. Asoc. - fizica neutronului, metodele clasice de aproximare inutile → metodele fizicii statistice → probleme economice - metodele analitice inoperante.

Problema principala in MC consta in estimarea valorii medii a unei variabile aleatoare in functie de eroarea admisibila si o probabilitate data.

Studiu de caz - Intocmirea planului de productie in functie de performantele echipamentului existent.

Atelier de tricotaje pentru copii - set de masini de tricotat noi - care in functie de tip, fire, indemanarea lucratorilor duce la rezultate diferite. Productia la 100 zile:

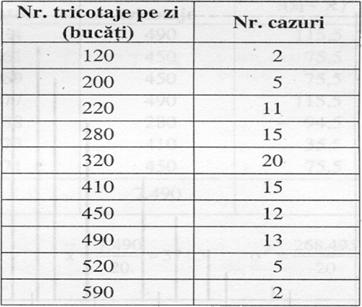
Se doreste cunoasterea performantelor atelierului.

MC - evaluarea performantelor plecand de la experimental pe cele 100 zile lucrate.

Calcul probabilitati:

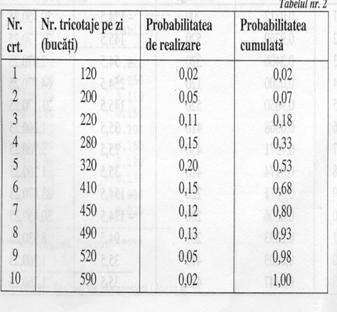
Generam 20 de numere aleatoare functia RAND():

x = AVERAGE(B1,B20) = SUM(B1,B20)/20 = 313.5

σ= DEVSTD(B1,B20) = 98.31609

C_V = 98.3169/313.5

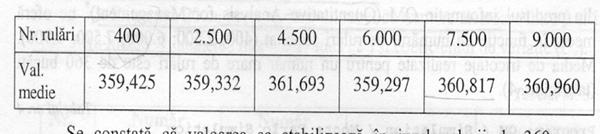
Se stabilizeaza in jurul lui 360.

Alte metode descriptive:

• Fluxuri informationale
• Analiza scenariilor
• Planificarea financiara
• Deciziile complexe de stocuri
• Analiza impactului mediului
• Previziuni
• Problema cozilor de asteptare
• Lanturi Markov.

Proces Markov - daca prezentul este cunoscut, viitorul nu depinde de trecut discrete/continue. => starea de la sfarsitul unui interval de timp t se poate determina in functie de starile din intervalele anterioare => lant Markov - determinat de distributia initiala a_j si matricea stohastica P.

Formalizare: E₁ , E_{2, .} - rezutate posibile - p₁ , p_{2, .} - probabilitati asociate. Probabilitatea unei succesiuni multiplicativa:

T.lanturilor M - o incercare depinde numai de precedenta si numai de ea.

Perechii E_j, E_k - probabilitatea de trecere p_jk daca s-a realizat E_j probabilitate de realizare a lui E_k. => Pr(E_j) = a_j - probabilitatea initiala. Probabilitatile de trecere E_j → E_k - matrice patratica cu suma pe linii = 1.

Studiu de caz a): Piata produselor lactate (lapte pasteurizat): A₁ - 3,2% grasime, A₂ - 2,8%, A₃ - 1,5%. Cota de participare in momentul 0 este: A₁ - 50%, A₂ - 35% A₃ - 15%. Coeficient de fidelitate constant de la o luna la alta: A₁ - 60%, A₂ - 70% A₃ - 80%, ceilalti parasesc produsul si se reorienteaza:

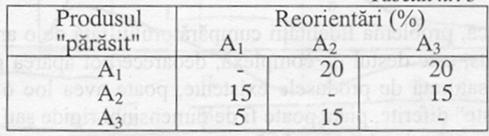
Determinarea evolutiei produselor pe 1 semestru.

P1. Matricea coeficientilor de trecere la 2 luni succesive:

P2. Distributia initiala:

P3. Deternmina ponderea pe piata a 3 produse dupa o luna:

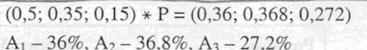
P4. Se determina ponderea dupa 2,3,4,5,6 luni =>

P5. Curbele evolutiilor:

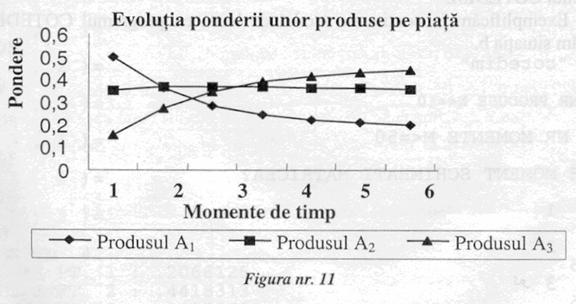
P7. Stabileste situatia produsului.

M1 → produs 1 in declin, pondere in scadere de la 50% la 20%, produsul 2 - maturitate - creste la 37% si se mentine la 36%, produsul 3 creste de la 15% la 44,1%.

b. Dupa 3 luni un nou sondaj cu rezultatele:

4. Simularea comportamentului (fidelitatii) cumparatorilor prin Monte Carlo.

1. Sa se simuleze comportamentul utilizatorilor produsului A₂ in urmatoarele 6 luni.
2. Sa se efectueze 30 de experimente de simulare a comportamentului utilizatorilor actuali a lui A₂ in raport cu momentul curent.

P1. Pentru fiecare linie a matricei probabilitatilor de tranzitie se determina distributia de probabilitate cumulata.

P2. Cu ajutorul probabilitatilor cumulate se asociaza fiecarui produs un interval de numere aleatoare uniform distribuite pe acest interval.

Exemplu:

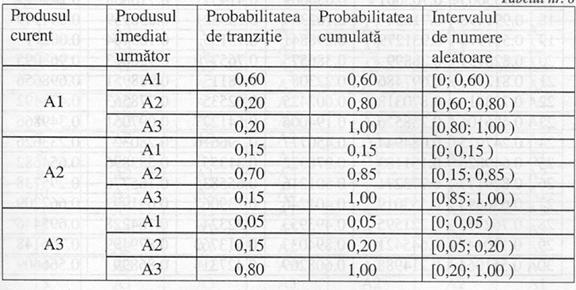
P3. Se genereaza un sir de 6 numere aleatoare U[0,1)→ 6*30=180.

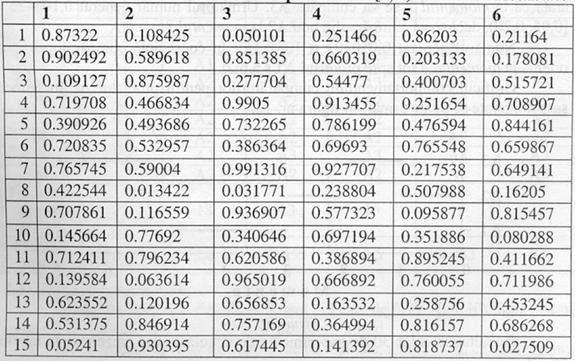
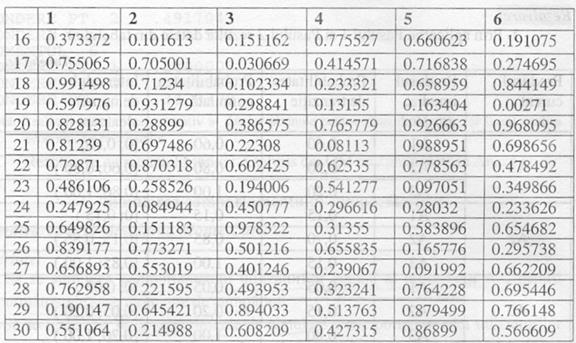
P4. Pentru fiecare numar generat se cauta intervalul (P2) caruia ii apartine si tipul de produs catre care se va orienta cumparatorul in functie de cumparatura care o preced (procesul Markov).

Cum se utilizeaza deci numerele aleatoare?

Momentul 1 - 0,87322, din [0.85; 1) → momentul 2 se cumpara produsul A₃, urmatorul numar 0,108425 din [0,05; 0,2) A₃ → A₂ → .

Se repeta experimentul de 30 de ori:

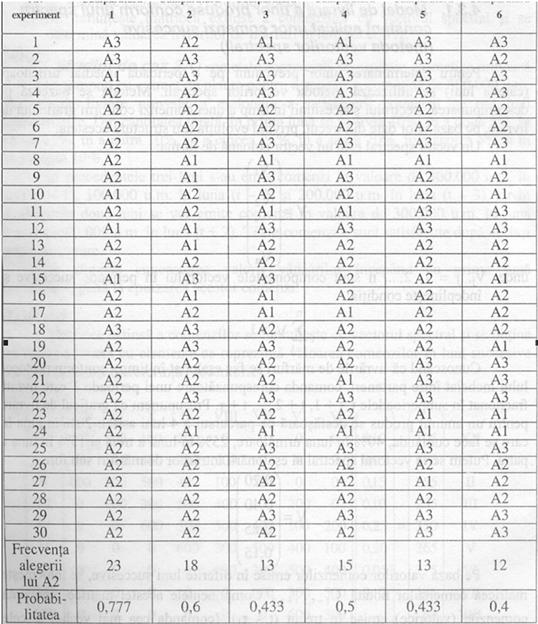
Fidelitatea fata de A2 -dupa o luna 0,777 (23/30), a doua 0,6 (18/30) .

Numar mare de simulari.

Exista un numar de metode descriptive nematematice. Exemplu: harta cognitiva (Eden & Akerman, 1998). Ajuta decidentul sa puna in evidenta factori calitativi care creeaza situatii cauzale in decizii neclare. Ajuta decidentii sa separe factorii relevanti de cei nerelevanti si sa invete mai mult despre problema. Un instrument de acest tip este Cognitive Explorer (Banxia Software Ltd, Anglia, www.banxia.com).

Alt model descriptiv este cel narativ. Metoda consta in nararea sau expunerea unor intamplari care sa ajute decidentul sa descopere partile ascunse ale problemei. Exemplu - elaborarea verdictelor juridice.