|
|
|
Studiul cuantic al oscilatorului liniar armonic
Din studiul mecanicii clasice se stie ca energia potentiala a unui punct material, de masa m0, aflat in campul unor forte elastice, este:
(4.52)
unde k este constanta elastica, iar este pulsatia proprie a oscilatorului. Daca energia oscilatorului este E, atunci din punct de vedere clasic particula oscileaza cu amplitudinea A. Intre energie si amplitudine exista relatia:
Din punct de vedere al mecanicii cuantice, pentru a obtine proprietatile oscilatorului armonic este necesara rezolvarea ecuatiei lui Schrodinger, in care energia potentiala este data de relatia (4.52):
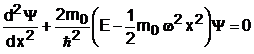(4.53)
Se poate obtine o forma mai simpla pentru aceasta ecuatie daca se introduce variabila:
Cu acasta notatie, avem egalitatile:
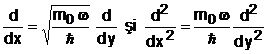
Cu ajutorul acestei formule putem calcula coeficientii A2, A3, A4, , in functie de coeficientii A0 si A1, care reprezinta constantele de integrare ale ecuatiei (4.57).
Deoarece patratul modulului functiei de unda este egal cu densitatea de probabilitate se impune ca aceasta functie sa fie finita pentru orice valoare a variabilei y. Se poate arata ca aceasta cerinta nu este indeplinita daca f(y) este o serie de puteri, ci numai daca f(y) este un polinom de grad v oarecare. Daca polinomul este de gradul v, din egalitatea Av+2=0 rezulta:
Daca egalitatea de mai sus este satisfacuta pentru o valoare oarecare finita a lui v, atunci functia de unda indeplineste conditiile necesare. Solutia (4.56) poate fi o functie de unda numai daca marimea ia valori discrete, adica energia oscilatorului armonic este cuantificata:
(4.61)
Rezulta
astfel ca, din punct de vedere cuantic, oscilatorul armonic poate avea
numai valori discrete ale energiei, iar diferenta dintre energiile a
doua nivele succesive este aceeasi, 
. Energia minima pe care o poate avea oscilatorul
armonic liniar este:
(4.62)
Aceasta
valoare se numeste energie de zero, deoarece valoarea energiei
oscilatorului tinde spre E0 atunci cand temperatura absoluta 
.
