
|
|
|
FIZICA PRECUANTICA (ORIGINILE FIZICII CUANTICE)
I RADIATIA TERMICA
A. BREVIAR
Radiatia electromagnetica emisa de suprafetele corpurilor, dependenta de temperatura suprafetei emitatoare, se numeste radiatie termica.
Principalele marimi fizice specifice radiatiei termice sunt:
a) emisivitatea (radianta)
integrala ![]() , definita prin expresia:
, definita prin expresia:
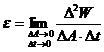 ,
,
unde ![]() este energia radiatiei emise in durata
este energia radiatiei emise in durata ![]() , de un element de suprafata cu aria
, de un element de suprafata cu aria ![]() ;
;
b) densitatile
spectrale (dupa frecventa ![]() , respectiv dupa lungimea de unda
, respectiv dupa lungimea de unda ![]() ) ale emisivitatii:
) ale emisivitatii:
![]() ,
, ![]() ,
,
unde ![]() si
si ![]() sunt respectiv contributiile la emisivitate ale radiatiilor
emise, din intervalele spectrale
sunt respectiv contributiile la emisivitate ale radiatiilor
emise, din intervalele spectrale ![]() , respectiv
, respectiv ![]() ;
;
c) densitatea volumica W si densitatile "spectralo-volumice" ![]() ,
, ![]() ale energiei radiatiei
termice
ale energiei radiatiei
termice
![]() ,
, ![]() ,
, ![]() ,
,
unde ![]() este energia radiatiei
termice dintr-un element spatial cu volumul
este energia radiatiei
termice dintr-un element spatial cu volumul ![]() , iar
, iar 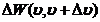 si
si ![]() sunt respectiv
contributiile la densitatea volumica a energiei a radiatiilor emise, din
intervalele spectrale
sunt respectiv
contributiile la densitatea volumica a energiei a radiatiilor emise, din
intervalele spectrale ![]() , respectiv
, respectiv ![]() ;
;
d) stralucirea (luminanta) B:
![]() ,
,
unde ![]() este
contributia la emisivitatea radiatiilor emise in interiorul unghiului solid
este
contributia la emisivitatea radiatiilor emise in interiorul unghiului solid ![]() , a carui directie centrala ("axa") formeaza unghiul
, a carui directie centrala ("axa") formeaza unghiul ![]() cu normala la suprafata
elementului
cu normala la suprafata
elementului ![]() care a emis radiatia,
care a emis radiatia,
e) coeficientul de absorbtie (absorbanta) ![]() , corespunzand lungimii de unda
, corespunzand lungimii de unda ![]() :
:
![]() ,
,
unde ![]() si
si ![]() reprezinta contributiile
intervalului spectral
reprezinta contributiile
intervalului spectral ![]() la energia
electromagnetica incidenta, respectiv absorbita de un acelasi element de
suprafata, in acelasi interval de timp
la energia
electromagnetica incidenta, respectiv absorbita de un acelasi element de
suprafata, in acelasi interval de timp ![]() .
.
Dupa cum coeficientul de absorbtie corespunzand suprafetei
unui corp este dependent de lungimea de unda a radiatiei electromagnetice
incidente: ![]() , respectiv este practic constant:
, respectiv este practic constant: ![]() (1), respectivul corp este numit "cu absorbtie (si emisie)
selectiva", respectiv "cenusiu". ¥n cazul in care coeficientul de absorbtie al
suprafetei unui corp este egal practic cu unitatea:
(1), respectivul corp este numit "cu absorbtie (si emisie)
selectiva", respectiv "cenusiu". ¥n cazul in care coeficientul de absorbtie al
suprafetei unui corp este egal practic cu unitatea: ![]() , respectivul corp este numit "negru".
, respectivul corp este numit "negru".
Radiatia termica dintr-o zona spatiala in cuprinsul careia
fiecare element de suprafata emite, in fiecare interval de timp ![]() , o cantitate de energie electromagnetica egala cu cea
absorbita in acelasi timp:
, o cantitate de energie electromagnetica egala cu cea
absorbita in acelasi timp: ![]() , se numeste radiatie termica de echilibru.
, se numeste radiatie termica de echilibru.
Prima lege a lui Kirchhoff afirma ca radiatia termica de echilibru
este omogena (![]() ), izotropa (stralucirea B este aceeasi in toate directiile) si
nepolarizata (P=0).
), izotropa (stralucirea B este aceeasi in toate directiile) si
nepolarizata (P=0).
Cea
de-a doua lege a lui Kirchhoff afirma ca
raporul dintre densitatea spectrala dupa lungimea de unda a emisivitatii
suprafetei unui corp si coeficientul de absorbtie ![]() corespunzator este o functie
"universala" (nu depinde de natura corpului si caracteristicile suprafetei emitatoare,
sau de alti parametri) de lungimea de unda
corespunzator este o functie
"universala" (nu depinde de natura corpului si caracteristicile suprafetei emitatoare,
sau de alti parametri) de lungimea de unda ![]() a radiatiei
electromagnetice de referinta si temperatura termodinamica T a suprafetei:
a radiatiei
electromagnetice de referinta si temperatura termodinamica T a suprafetei: ![]() .
.
¥ntre radianta integrala
(emisivitatea) ![]() , stralucirea B si densitatea volumica W a energiei
electromagnetice corespunzand radiatiei termice de echilibru, precum si densitatile
lor spectrale, exista relatiile:
, stralucirea B si densitatea volumica W a energiei
electromagnetice corespunzand radiatiei termice de echilibru, precum si densitatile
lor spectrale, exista relatiile:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
a) radiatia integrala
(emisivitatea ) ![]() , stralucirea B si densitatea volumica W a
energiei radiatiei termice de echilibru;
, stralucirea B si densitatea volumica W a
energiei radiatiei termice de echilibru;
b) densitatile spectrale corespunzand marimilor fizice de mai sus.
Legile empirice ale radiatiei corpului negru sunt
1) radianta integrala (emisivitatea) suprafetei unui corp negru este proportionala cu puterea a 4-a a temperaturii termodinamice a suprafetei (legea Stefan-Boltzmann):
![]() ,
,
unde ![]() este constanta
universala a lui Stefan-Boltzmann,
este constanta
universala a lui Stefan-Boltzmann,
2) lungimea de unda ![]() pentru care densitatea
spectrala a emisivitatii unui corp negru atinge o valoare maxima pentru o
temperatura termodinamica data T a suprafetei emitatoare este invers proportionala
cu aceasta temperatura (legea "deplasarii"
a lui Wien):
pentru care densitatea
spectrala a emisivitatii unui corp negru atinge o valoare maxima pentru o
temperatura termodinamica data T a suprafetei emitatoare este invers proportionala
cu aceasta temperatura (legea "deplasarii"
a lui Wien):
![]() ,
,
unde ![]() este constanta
universala a lui Wien,
este constanta
universala a lui Wien,
3) densitatea spectrala a emisivitatii unui corp depinde de lungimea de unda 1 a radiatiei monocromatice de referinta si de temperatura termodinamica T a suprafetei emitatoare conform expresiei:
![]() ,
,
unde ![]() si
si ![]() sunt constantele
universale ale lui Wien
sunt constantele
universale ale lui Wien![]() (legea Wien a densitatii spectrale a emisivitatii,
valabila in domeniul ultraviolet al spectrului pentru temperaturi ale suprafetei
radiante de ordinul a
(legea Wien a densitatii spectrale a emisivitatii,
valabila in domeniul ultraviolet al spectrului pentru temperaturi ale suprafetei
radiante de ordinul a ![]() K),
K),
4) densitatea spectrala a emisivitatii unui corp negru este proportionala cu temperatura termodinamica T a suprafetei sale si invers proportionala cu puterea a 4-a a lungimii de unda de referinta:
![]() ,
,
unde ![]() J/K este constanta lui
Boltzmann (legea Rayleigh-Jeans,
valabila in domeniul infrarosu al spectrului, pentru temperaturi
J/K este constanta lui
Boltzmann (legea Rayleigh-Jeans,
valabila in domeniul infrarosu al spectrului, pentru temperaturi ![]() K ale suprafetei corpului negru).
K ale suprafetei corpului negru).
Legea Planck a radiatiei termice de echilibru a unui corp negru
afirma ca dependenta densitatii spectrale a emisivitatii de temperatura termodinamica
a suprafetei radiante si lungimea de unda ![]() de referinta este data
de expresia:
de referinta este data
de expresia:
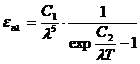 .
.
Energia
medie a unui mod ondulatoriu stationar total-polarizat, de lungime de unda ![]() si frecventa
si frecventa ![]() , este data de expresia:
, este data de expresia: 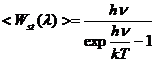 , unde h este constanta lui Planck, definita prin prima constanta
, unde h este constanta lui Planck, definita prin prima constanta ![]() a lui Wien in baza
expresiei:
a lui Wien in baza
expresiei:
![]() .
.
Se cere :
a) sa se deduca legea Stefan - Boltzmann pornind de la legea Planck a radiatiei termice de echilibru a corpului negru;
b) sa
se calculeze constanta universala ![]() a lui Stefan si
Boltzmann pornind de la valorile constantelor universale C1 si C2
ale lui Wien.
a lui Stefan si
Boltzmann pornind de la valorile constantelor universale C1 si C2
ale lui Wien.
Se cere :
a) sa se constate in ce conditii legea Planck se particularizeaza in legile empirice Wien, respectiv Rayleigh - Jeans ale densitatii spectrale a emisivitatii corpului negru;
b) sa se deduca legea empirica a lui Rayleigh - Jeans pornind de la teorema echipartitiei energiei pe grade de libertate a fizicii statistice clasice;
c) stiind
ca rezultatele experimentale privind radiatia termica a corpului
negru sunt descrise de legea lui Planck, sa se constate in ce masura legea
empirica a lui Rayleigh - Jeans concorda cu rezultatele experimentale
la limita ![]() ;
;
d) sa se deduca semnificatia statistica a legii lui Planck.
Se cere :
a) sa se deduca legea "deplasarii" a lui Wien, pornind de la legea Planck a radiatiei termice de echilibru a corpului negru;
b) sa se calculeze constanta universala a lui Wien, pornind de la valoarea constantei universale C2 a radiatiei termice.
Sa se deduca :
a) lungimile de unda ale modurilor ondulatorii stationare pentru o cavitate cubica de latura a;
b)expresia
densitatii spectralo - volumice a numarului de stari ondulatorii
stationare intr-o cavitate pentru cazul uzual cand latura cavitatii ![]() mm, iar lungimea de unda de referinta
mm, iar lungimea de unda de referinta ![]() mm.
mm.
Pornind de la formulele Fresnel scrise pentru incidenta normala a unei unde electromagnetice din aer pe suprafata unui metal, sa se deduca :
a) dependenta de lungimea de unda, in domeniile vizibil si infararosu, a coeficientului de absorbtiei al radiatiilor electromagnetice de catre metal;
b) expresia densitatii spectrale a emisivitatii unui metal.
Sa se deduca :
a) dependenta
de temperatura a emisivitatii (radiantei) integrale ![]() a unui metal,
stiind ca rezistivitatea metalelor variaza direct
proportional cu temperatura termodinamica;
a unui metal,
stiind ca rezistivitatea metalelor variaza direct
proportional cu temperatura termodinamica;
b) lungimea
de unda ![]() pentru care densitatea
spectrala
pentru care densitatea
spectrala ![]() a
emisivitatii unui metal atinge, pentru o temperatura data a
suprafetei metalului, o valoare maxima.
a
emisivitatii unui metal atinge, pentru o temperatura data a
suprafetei metalului, o valoare maxima.
Pentru lungimile de unda ![]() satisfacand conditia
satisfacand conditia ![]() (unde
(unde ![]()
este
rezistivitatea electrica, iar ![]() este permitivitatea),
deci - pentru metale - in domeniile vizibil, infrarosu, al microundelor s.a.m.d.,
dependenta de lungimea de unda a radiatiei electromagnetice incidente a
coeficientului de absorbtie al unui metal este data de formula lui Drude:
este permitivitatea),
deci - pentru metale - in domeniile vizibil, infrarosu, al microundelor s.a.m.d.,
dependenta de lungimea de unda a radiatiei electromagnetice incidente a
coeficientului de absorbtie al unui metal este data de formula lui Drude:
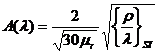 ,
,
unde ![]() este valoarea numerica,
in unitati SI, a raportului
este valoarea numerica,
in unitati SI, a raportului ![]() .
.
Dependenta
de lungimea de unda (in domeniile care satisfac cerinta ![]() ) a densitatii spectrale a emisivitatii unui metal este
descrisa de legea lui Aschkinass:
) a densitatii spectrale a emisivitatii unui metal este
descrisa de legea lui Aschkinass:
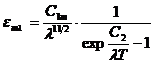 ,
,
unde constanta (specifica metalului) lui Aschkinass are valoarea numerica:
|
Pentru metalele a caror rezistivitate depinde direct proportional
de temperatura termodinamica, dependenta de temperatura suprafetei unui metal a
emisivitatii (radiantei) integrale a acestuia este data de legea Lummer-Kurlbaum: ![]() , unde valoarea numerica a constantei
, unde valoarea numerica a constantei ![]() (specifica fiecarui
metal) este:
(specifica fiecarui
metal) este:
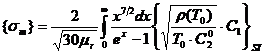 ,
,
unde ![]() este temperatura
termodinamica de referinta fixata.
este temperatura
termodinamica de referinta fixata.
Dependenta de temperatura suprafetei unui metal a
lungimii de unda pentru care densitatea spectrala a emisivitatii metalului
atinge valoarea maxima este descrisa de legea
Lummer-Pringsheim: ![]() , unde
, unde ![]() este o constanta
universala (avand o aceeasi valoare:
este o constanta
universala (avand o aceeasi valoare: ![]() pentru toate
metalele).
pentru toate
metalele).
Principalele marimi fotometrice sunt:
a)Fluxul luminos ![]() (emis sau primit de un
corp) prin care se intelege fluxul de energie electromagnetica, evaluat prin
senzatia luminoasa produsa.
(emis sau primit de un
corp) prin care se intelege fluxul de energie electromagnetica, evaluat prin
senzatia luminoasa produsa.
a) Intensitatea luminoasa I definita prin relatia:
![]()
unde ![]() este fluxul luminos
emis in unghiul solid elementar
este fluxul luminos
emis in unghiul solid elementar ![]() .
.
c)Lungimea de unda
![]() corespunzand maximului
vizibilitatii relative este acea lungime de unda pentru care - in regimul de
observatie respectiv - raportul:
corespunzand maximului
vizibilitatii relative este acea lungime de unda pentru care - in regimul de
observatie respectiv - raportul:
![]()
este
maxim, ![]() si
si ![]() fiind contributiile radiatiilor
(unei surse) din intervalul spectral
fiind contributiile radiatiilor
(unei surse) din intervalul spectral ![]() la valoarea fluxului
luminos, respectiv energetic, al sursei (
la valoarea fluxului
luminos, respectiv energetic, al sursei (![]() variaza cu regimul de observatie:
variaza cu regimul de observatie: ![]() in spectrul diurn,
in spectrul diurn, ![]() in regim crepuscular,
etc.)
in regim crepuscular,
etc.)
d)Fluxul (puterea) efectiv(a) ![]() , corespunzand - intr-un anumit regim de observatie - radiatiei
electromagnetice compuse emise de o sursa, este egal cu fluxul energetic
, corespunzand - intr-un anumit regim de observatie - radiatiei
electromagnetice compuse emise de o sursa, este egal cu fluxul energetic ![]() corespunzand radiatiilor
monocromatice
corespunzand radiatiilor
monocromatice ![]() care - fiind emise de
o sursa asezata in acelasi loc - ar produce un efect fiziologic identic (o aceesi
valoare a intensitatii luminoase) cu acela determinat de radiatia compusa.
care - fiind emise de
o sursa asezata in acelasi loc - ar produce un efect fiziologic identic (o aceesi
valoare a intensitatii luminoase) cu acela determinat de radiatia compusa.
e)Densitatea spectrala ![]() a fluxului efectiv definita condform relatiei:
a fluxului efectiv definita condform relatiei:
![]() ,
,
unde ![]() este contributia la
fluxul efectiv a radiatiilor electromagnetice avand numerele de unda cuprinse
in intervalul spectral ingust
este contributia la
fluxul efectiv a radiatiilor electromagnetice avand numerele de unda cuprinse
in intervalul spectral ingust ![]() .
.
f)Efectivitatea luminoasa (vizibilitatea) relativa definita prin relatia:
![]() f(
f(![]() , regim de observatie)
, regim de observatie)
g) Echivalentul fotometric al fluxului efectiv definit prin relatia:
![]() ,
,
unde ![]() si
si ![]() sunt fluxul luminos,
respectiv fluxul efectiv emis de un element de arie
sunt fluxul luminos,
respectiv fluxul efectiv emis de un element de arie ![]() al unei surse, in
interiorul unui unghi solid de marime
al unei surse, in
interiorul unui unghi solid de marime ![]() . Echivalentul fotometric al fluxului efectiv depinde
intrucatva (slab) de regimul de observatie, precum si de observator.
. Echivalentul fotometric al fluxului efectiv depinde
intrucatva (slab) de regimul de observatie, precum si de observator.
h) Luminanta (stralucirea) L
in directia formand unghiul ![]() cu normala la suprafata
sursei (de mici dimensiuni):
cu normala la suprafata
sursei (de mici dimensiuni):
![]() ,
,
unde ![]() este fluxul luminos
emis de elementul
este fluxul luminos
emis de elementul ![]() al sursei, in
interiorul unghiului solid elementar
al sursei, in
interiorul unghiului solid elementar ![]() in jurul directiei
respective, iar
in jurul directiei
respective, iar ![]() este intensitatea
luminoasa emisa - in directia
este intensitatea
luminoasa emisa - in directia ![]() - de elementul
- de elementul ![]() al sursei.
al sursei.
i) Densitatea spectrala
![]() a luminantei, definita conform relatiei:
a luminantei, definita conform relatiei:
![]() ,
,
unde ![]() este contributia la
luminanta a radiatiilor electromagnetice avand numerele de unda situate in
intervalul spectral ingust
este contributia la
luminanta a radiatiilor electromagnetice avand numerele de unda situate in
intervalul spectral ingust ![]() ; conform relatiilor de mai sus al breviarului, avem:
; conform relatiilor de mai sus al breviarului, avem:
![]() .
.
Principalele unitati (in sistemul "international") fotometrice sunt:
a) candela (simbol
cd) definita drept intensitatea luminoasa emisa in directia normala de o portiune
- de arie egala cu ![]() - a suprafetei unui
corp negru aflat la temperatura de solidificare a platinei (T=2044 K), sub o
presiune de 101325
- a suprafetei unui
corp negru aflat la temperatura de solidificare a platinei (T=2044 K), sub o
presiune de 101325 ![]() .
.
b)lumenul (simbol lm) definit drept fluxul luminos emis in unitatea de unghi solid (steradian) de o sursa de lumina, punctiforma si uniforma, avand intensitatea luminoasa de o candela;
c)wattul efectiv (luminos) (simbol Wl) definit drept fluxul efectiv
al unei surse de radiatii electromagnetice compuse pentru care efectul
fiziologic (intensitatea luminoasa) este identic cu cel produs de o sursa
monocromatica ![]() , asezata in acelasi loc si emitand - cu aceeasi distributie
unghiulara a energiei electromagnetice - fluxul energetic de 1 W;
, asezata in acelasi loc si emitand - cu aceeasi distributie
unghiulara a energiei electromagnetice - fluxul energetic de 1 W;
d) nitul (simbol nt) definit drept luminanta uniforma a unei surse
plane de lumina, de arie egala cu 1 ![]() a carei intensitate
luminoasa in directia normala este de o candela.
a carei intensitate
luminoasa in directia normala este de o candela.