
|
|
|
R.1 In punctul C ![]() ;
; ![]() (1) si
(1) si ![]() (2). Impartite relatiile conduc la
(2). Impartite relatiile conduc la ![]()
![]()
![]()
![]()
![]() . R: a
. R: a
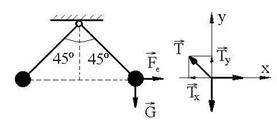
R.2 Conditiile de echilibru ale sferei B:
Ox: ![]() :
: ![]() (1) Oy: mg
= Tcos45o (2) Din triunghiul OAB
(1) Oy: mg
= Tcos45o (2) Din triunghiul OAB ![]() de unde d = 2l
sin45o. (3) Din
relatiile (1), (2) si (3)
de unde d = 2l
sin45o. (3) Din
relatiile (1), (2) si (3) ![]()
![]() . R:e
. R:e
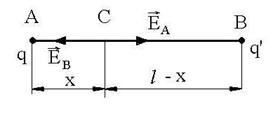
R.3 EA = EB ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
. ![]()
![]()
![]() . R: e
. R: e
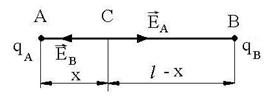
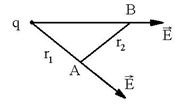
R.4 LAB ![]() nu depinde de drumul
parcurs
nu depinde de drumul
parcurs 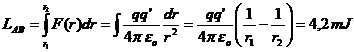 . R: a.
. R: a.
R.5 ![]() (1)
(1) ![]()
![]()
![]() (2). Rezolvarea
sistemului de ecuatii format din (1) si (2) conduce la
(2). Rezolvarea
sistemului de ecuatii format din (1) si (2) conduce la ![]() si
si ![]() . R:a
. R:a
R.3. 2..6 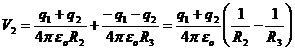 . Pe sfere pe langa sarcinile incarcate apar
si sarcinile prin influenta. V2
= 600 V. R: e.
. Pe sfere pe langa sarcinile incarcate apar
si sarcinile prin influenta. V2
= 600 V. R: e.
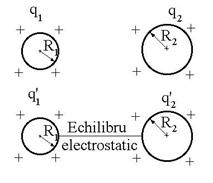
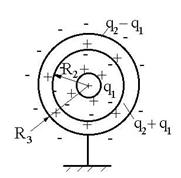
R.7![]()
![]()
![]() .
. ![]()
![]()
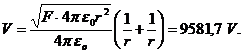 R: a.
R: a.
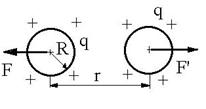
Fig.R.7
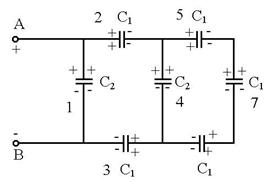
R.8 Dupa modul cum sunt incarcati
cu sarcini condensatorii sunt grupati astfel: condensatorii C5, C6, C7
![]() serie CR1. CR1 paralel cu C4
serie CR1. CR1 paralel cu C4
![]() CR2. Condensatorii C2
CR2. Condensatorii C2
![]() CR2, C3
CR2, C3![]() serie
serie ![]() CR3. CR3 paralel cu C1
CR3. CR3 paralel cu C1 ![]() Cr.
Cr. ![]() ;
; ![]() . CR3
. CR3 ![]()
![]()
![]()
![]() .
. ![]() . R: a
. R: a
R.9 Condensatorii dupa modul cum s-au
incarcat cu sarcini sunt in serie. E1
+ E2 = U1 + U2 ![]() ;
; ![]() ; Q1 = Q2 = Q de unde
; Q1 = Q2 = Q de unde 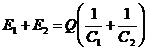
![]()
![]() de unde
de unde ![]() . R:c.
. R:c.
R.2.3.10![]()
![]()
![]()
![]()
![]() . R: b.
. R: b.
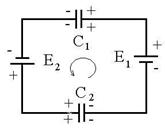
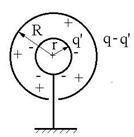
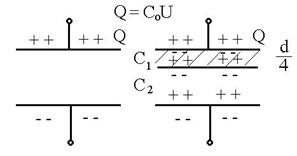
Fig.R.11
|
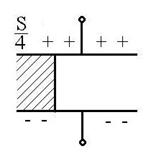
Fig.R.12 |
R.11 Q = CoU. Prin introducerea dielectricului se
formeaza doi condensatori legati in serie. ![]() ;
; ![]() :
: ![]() ;
; 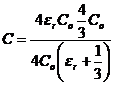 :
:![]() ;
; ![]()
![]() U = 16 kV. R: e.
U = 16 kV. R: e.
R.12 Sistemul nou format are
doi condensatori (![]() ) legati in paralel.
) legati in paralel. ![]()
![]()
![]() :
: ![]()
![]() ,
, ![]()
![]()
![]() . R: a.
. R: a.
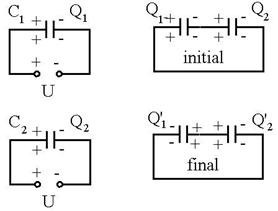
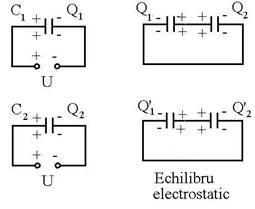
R.13 ![]() ;
; ![]() ,
, ![]()
![]()
![]()
![]()
![]()
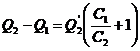
![]()
![]() :
: ![]() .
. ![]() ,
, 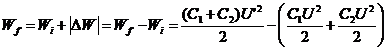
![]() Wi =
3750 J; Wf
= 833 J,
Wi =
3750 J; Wf
= 833 J, ![]() R: d.
R: d.
R.14 ![]() :
: ![]()
![]()
![]() ,
, ![]() ;
; ![]() .
. 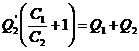 :
: ![]() ;
; ![]() .
. ![]() ;
; 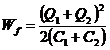
![]() Wi = Wf
Wi = Wf
![]()
![]() R:a.
R:a.
R.15 ![]() ,
, ![]() , Q = UAOCr = (VA
- VO=Cr, Q = -24.10-4
C.
, Q = UAOCr = (VA
- VO=Cr, Q = -24.10-4
C. ![]() . R:e.
. R:e.
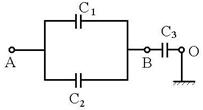
Fig.R.15
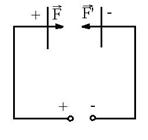
R.16 L =
W = Fmd = ![]()
![]()
![]()
![]() Fm = 1 N. R: a.
Fm = 1 N. R: a.
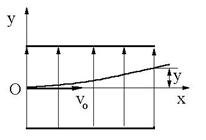
R.17 Ox: x = l
= vo t; Oy: ![]() :
: ![]() .
. ![]()
![]()
![]()
![]()
![]() . R: d.
. R: d.
R.18 Ox: vOx = vx; vOx = vocos30o; vx
= vocos60o; vocos30o = v cos60o:
x = l = vocos30ot ![]()
![]() . Oy: vy = vOy + ayt
. Oy: vy = vOy + ayt ![]()
![]()
![]()
![]() (1)
(1) ![]() (2)
(2) ![]() . R:b.
. R:b.
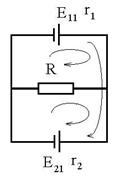
R.19 I = I1 + I2; E1 = r1I1 + I R; E2 = I2r2 + IR, ![]() E1 - E2 = I1r1
- I2r2 I1r1 = I2r2
(E1 = E2)
E1 - E2 = I1r1
- I2r2 I1r1 = I2r2
(E1 = E2) ![]()
![]() ; I = 1,5 A. R: c.
; I = 1,5 A. R: c.
R.20 ![]() ;
; ![]() ,
, ![]() (RA = 0)
(RA = 0) ![]() r = 0,5
r = 0,5 ![]() . R: a.
. R: a.
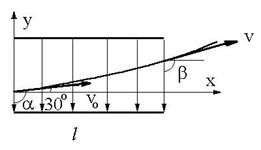
Fig.R.18
|
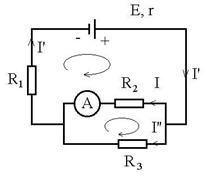
Fig.R.21 |
R.21 k ![]() inchis. Intr-un interval de timp foarte mic se incarca
condensatorii dupa care joaca rol de intrerupator (nu mai trec
sarcini pe acea latura)E = I(R2
+ R1 + r):
inchis. Intr-un interval de timp foarte mic se incarca
condensatorii dupa care joaca rol de intrerupator (nu mai trec
sarcini pe acea latura)E = I(R2
+ R1 + r): ![]()
![]()
![]() .
. ![]() , Q = CUAB,
, Q = CUAB, ![]() , Q = 8,34.10-4
C. R:
c.
, Q = 8,34.10-4
C. R:
c.
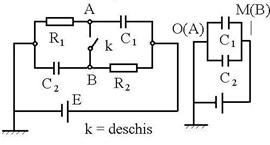
R.22 VA = Vo,
I1 = 0 si VB = VM, I2
= 0 ![]() Toata tensiunea cade pe condensator.
Toata tensiunea cade pe condensator. ![]() , Q1 = EC1 = 54.10-6 C. k
, Q1 = EC1 = 54.10-6 C. k ![]() inchis. E =I(R1
+ R2):
inchis. E =I(R1
+ R2): ![]() ;
; ![]() ;
; ![]() ,
, ![]() ,
, ![]() . R:c.
. R:c.
|
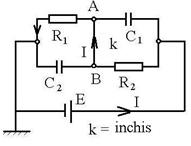
Fig.R.23 |
R.23 ![]() (1)
(1) ![]() :
: ![]() (2)
(2) ![]() E = 3 V. R:c.
E = 3 V. R:c.
R.24 Rezistentele pe fiecare latura
fiind egale inseamna ca VB
= VC. Datorita
acestui fapt prin rezistenta de pe diagonala nu trece curent ( ca
si cum nu ar mai fi). In punte avem RAB
serie cu RBD si RAC serie cu RCB. Cele doua
rezistente echivalente sunt legate in paralel RC = R, ![]() . R : b.
. R : b.
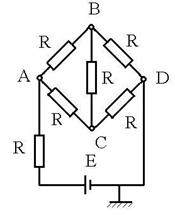
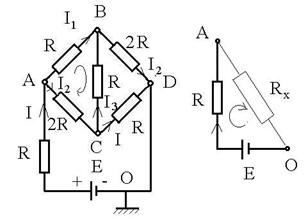
R.25 Datorita simetrie, laturile opuse ale
puntii sunt strabatute de aceeasi curenti. I = I1
+I2 (1) I2 = I1 + I3
(2) I1R = I3R + I22R ![]() I1 = I3
+ 2I2 (3)
I1 = I3
+ 2I2 (3) ![]()
![]() ,
, ![]() , E = IR + I1R + 2RI2
, E = IR + I1R + 2RI2
![]()
![]() . R: b.
. R: b.
R.26 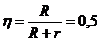 ; P = RI2 =
; P = RI2 = ![]() ; P = Pmax cand
; P = Pmax cand ![]()
![]() (R+r)2-2R(R+r)=0 de unde R = r . R:a
(R+r)2-2R(R+r)=0 de unde R = r . R:a
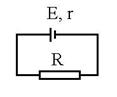
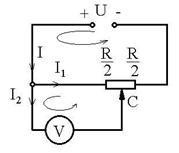
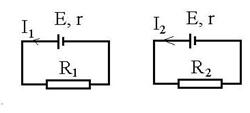
R.27 I1
+ IV = I; ![]() ;
; ![]() ; U = 55,4 V. R:
c
; U = 55,4 V. R:
c
R.28![]() :
: ![]()
![]()
![]()
![]()
![]() . R:d.
. R:d.
R.29 Uo = Uf
+ U; 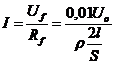 ;
; ![]() ;
; ![]() ;
; ![]()
![]()
![]()
![]()
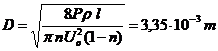 . R:a.
. R:a.
R.30 B = B1 + B2 + B3; 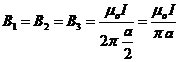 :
: ![]() ,
, ![]() . R: e.
. R: e.
R.31 ![]() ; Oy:
; Oy: ![]() ; Ox:
; Ox: ![]() ;
; 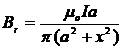 ;. R: a.
;. R: a.
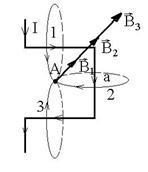
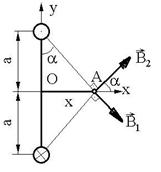
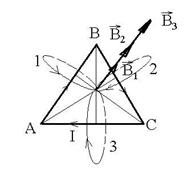
R.32 Se observa ca
inductiile magnetice generate de curenti ce trec prin cele trei
laturi au aceeasi directie, acelasi sens si aceeasi
valoare numerica. ![]() :
: ![]() ;
; ![]()
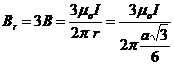
![]()
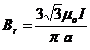 . R:b.
. R:b.
R.33 ![]() . R: b.
. R: b.
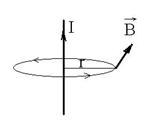
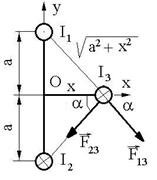
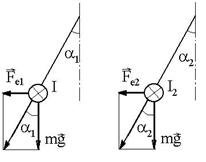
R.34 F23 = F13 = F: Ox ![]() ; Oy:
; Oy: ![]() .
. 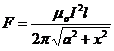
![]()
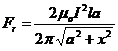
![]()
![]() . R: a.
. R: a.
R.35 ![]() (1)
(1) ![]() (2) Din relatiile
(1) si (2)
(2) Din relatiile
(1) si (2) ![]()
![]()
![]()
![]() . R:c.
. R:c.
R.36 ![]() :
: ![]() ;
; ![]() ; P= Fmecv
; P= Fmecv ![]()
![]() = 6.10-2
W.
= 6.10-2
W.
R:e.
R.37 ![]() R: e.
R: e.
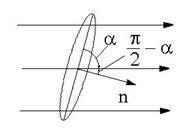
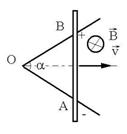
R.38 ![]() ; U = RI;
; U = RI; ![]()
![]()
![]()
![]()
![]() ;
; 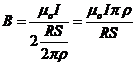 ;
; ![]()
![]()
![]()
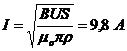 . R:e.
. R:e.
R.39 ![]() ;
; ![]() ;
; ![]()
![]()
![]() R: a.
R: a.
R.40 ![]() ;
; ![]() :
: ![]() ,
, ![]()
![]()
![]()
![]() :
: ![]() . R:b.
. R:b.
R.41 ![]() , din
, din ![]() ,
, ![]() , vt = OD.
, vt = OD. ![]() ;
; ![]() ,
,
R = r(OA+OB+AB),
OA = OB : ![]() :
: 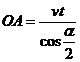 .
. 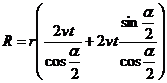
![]()
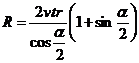 .
. 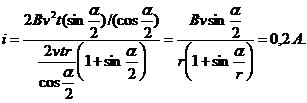 R:b.
R:b.
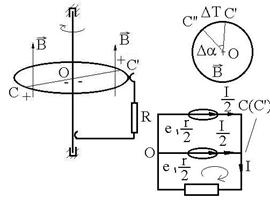
R.42 Prin rotirea barei pe inel, datorita
faptului ca bara taie liniile de camp magnetic la bornele OC si OC
apar t.e.m. induse. Cele doua portiuni ale barei OC si OC sunt
echivalente cu doua surse (e, r/2). ![]() ;
; ![]()
![]()
![]() ,
, ![]() ,
, ![]() ;
; ![]() ;
; ![]()
![]()
![]() .
. ![]() ,
, ![]() ,
, ![]()
![]()
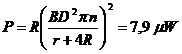 . R: a.
. R: a.

R.43 Conductorul ce se misca este
echivalent cu o sursa cu t.e.m. e
si rezistenta r. Atunci ![]() (1) e =
Ir + I1R1 (2) e = Ir
+ I2R2 (3) si e = Blv
(1) e =
Ir + I1R1 (2) e = Ir
+ I2R2 (3) si e = Blv
![]()
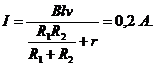 R:b.
R:b.
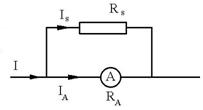
R.44 ![]() ; I = IA +
IS : IARA
= ISRS;
; I = IA +
IS : IARA
= ISRS; ![]() . R:e
. R:e
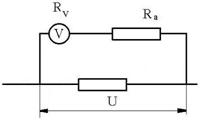
R.45 U = 25; I = 25 mA; U = UA
+ Ua: UA = RAI; Ua
= RaI; ![]() . R: a
. R: a
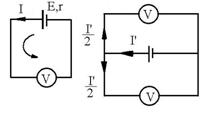
R.46 E = IR
+ IRV; (1) IRV = U; ![]() ; (2)
; (2) 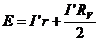 :
: ![]() ;
; ![]() (3) Din relatiile (2) si (3) E =
112,5 V. R: a
(3) Din relatiile (2) si (3) E =
112,5 V. R: a
R.47 m = KIt:
![]() ;
; ![]() . R: c
. R: c
R.48 ![]() ; mCu =
; mCu = ![]() de unde
de unde ![]() . R:d
. R:d
R.49 Din legea dupa care variaza curentul se
observa ca I scade liniar. ![]() : IM=Io=10A; Imin
= 6 A; Im = 8 A; m = KIt
= 0,525 g. R: a
: IM=Io=10A; Imin
= 6 A; Im = 8 A; m = KIt
= 0,525 g. R: a
R.50 m = KIt; mt = 40KIt = 6,43 kg. R:a
R.51 Din caracteristica ![]() . Pe circuit aplicand legea lui Kirchhoff se obtine:
. Pe circuit aplicand legea lui Kirchhoff se obtine: ![]()
![]() E = 22 V. R: b
E = 22 V. R: b
R.52 P = RdI2 = 1,21 W. R: a
R.53 Din graficul caracteristicii curent - tensiune
se observa: Eo = 0,7 V. Eo
![]() tensiunea de deschidere a diodei: Rd = 0. Aplicand legea lui Kirchhoff pe ochiul de
circuit se obtine: E = Eo+IR
tensiunea de deschidere a diodei: Rd = 0. Aplicand legea lui Kirchhoff pe ochiul de
circuit se obtine: E = Eo+IR ![]()
![]() R: a
R: a
R.54 Din graficul
caracteristicii rezulta: Eo
= 0,3 V, ![]() , E = Eo +I(Rd + R)
, E = Eo +I(Rd + R) ![]()
![]() . Uo = Eo
+IRd = 0,8 V. R: d
. Uo = Eo
+IRd = 0,8 V. R: d
|
Fig.R.55 |
R.55 Rd = 10 ![]() ;
; ![]() ; u = i(Rd
+ R);
; u = i(Rd
+ R); ![]() ;
; ![]() ;
; ![]() . R:
a
. R:
a
R.56 Dioda conduce pentru tensiunea ce
realizeaza o polarizare directa. ![]() ; u2 = uD +uRS
; u2 = uD +uRS
de unde u2 -uRS
![]() 0,
0, ![]() ,
, ![]() ;
; ![]() . R:c
. R:c
R.57 pentru t1 (+)A
si (-)B polarizare directa.![]() :
: ![]()
Pentru t2 (-)A si (+)B prin dioda
nu trece curent. R1 = 3R; ![]() . Se obtine
. Se obtine
Qt = Q1 + Q2 = 11,2 J. R: a
R.58 ![]() sau
sau ![]() :
: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.![]() ;
; ![]() . R:b
. R:b
R.59 ![]() ;
; ![]() :
: ![]() : R: b
: R: b
R.60 ![]() ;
; ![]()
![]()
![]() spire. R: a
spire. R: a
R.61 ![]() ;
; ![]()
![]()
![]() .
R: a.
.
R: a.
R.62 ![]() ,
, ![]() :
: ![]()
![]()
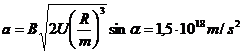 .
.
R: a
R.63 In zona campului magnetic miscarea
particulei se face pe un cerc, ![]() ;
;
![]() , (din triunghiul OAD). Rezulta
, (din triunghiul OAD). Rezulta ![]() . R: c
. R: c
R.64 In solenoid ![]() . Conditia de a iesi tot pe axa este ca l = nh,
(h este pasul).
. Conditia de a iesi tot pe axa este ca l = nh,
(h este pasul).
![]() :
: ![]()
![]()
![]()
![]()
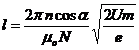
![]()
![]() : I = Imax : n = 1
: I = Imax : n = 1 ![]()
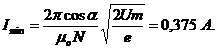 R: c
R: c
R.65
La rezonanta ![]() . R: a
. R: a
R.66![]()
![]()
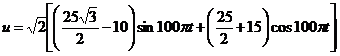 (1)
(1)
![]() (2)
(2) ![]()
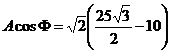 si
si ![]() de unde A = 42,2 = Umax
de unde A = 42,2 = Umax ![]()
![]() . R: b
. R: b
R.67
![]() ;
; ![]()
![]()
![]() . R:a
. R:a
R.68 ![]()
![]()
![]() . R: d
. R: d
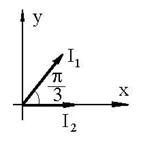
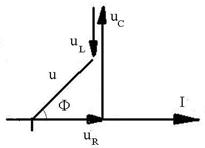
R.69
![]() ,
, ![]() ;
; ![]() ,
, ![]() :
: ![]() , UR = U
, UR = U ![]()
![]()
![]()
![]()
fig.R.69,a ![]() :
: ![]()
![]() ;
; 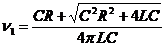
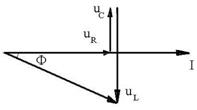
fig.R.70,b ![]()
![]()
![]() ;
; 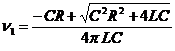
![]() R: e
R: e
R.70
Pmax = RI2 si ![]() ,
, ![]() : la rezonanta I
= IR
: la rezonanta I
= IR ![]()
![]()
![]()
![]()
![]()
![]() .
. ![]()
![]()
![]() :
: ![]()
![]()
![]() :
: ![]() si
si ![]() . R: a
. R: a
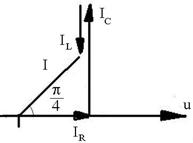
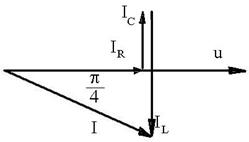
R.71 ![]()
![]()
![]()
![]()
![]() . R: d
. R: d
R.72P = RI2: ![]() ,
, ![]() ; U = 100 V
; U = 100 V ![]()
![]()
![]() P = 50.2= 100 W. R:e
P = 50.2= 100 W. R:e
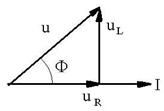
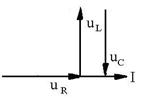
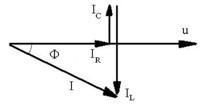
R.73 U =
UR ![]() UL = UC
UL = UC ![]()
![]()
![]()
![]() . R:
a
. R:
a
R.74 ![]() :
: ![]() ,
, ![]() R:c
R:c
R.75 ![]() R:
a
R:
a
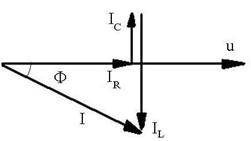
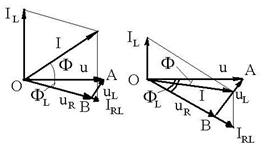
R.76 ![]() .
R: d
.
R: d
R.77 ![]()
![]() C1 ;
C1 ; ![]()
![]() C2
C2
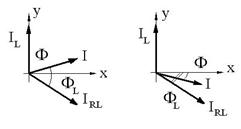
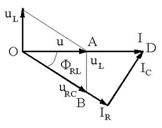
![]() (fig.,c si
fig.,d)
(fig.,c si
fig.,d) ![]() ;
; ![]()
Ox: ![]() (1) Oy:
(1) Oy: ![]() (2)
(2)
Ox : ![]() (3) Oy:
(3) Oy: ![]() (4)
(4)
![]() ;
; 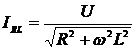 Din relatiile (1)
si (2)
Din relatiile (1)
si (2) ![]()
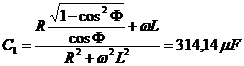 .
.
Din
relatiile (3) si (4) ![]()
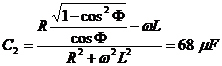 . R: a
. R: a
R.78 ![]()
![]() (1)
(1)
![]()
![]() (2) Din relatiile
(1) si (2) rezulta
(2) Din relatiile
(1) si (2) rezulta
![]() . R: a
. R: a
R.79 ![]()
![]()
![]() : R:d
: R:d
R.80 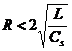
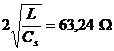
![]() . R:a
. R:a
R.81 ![]()
![]()
![]() . R: a
. R: a
R.82 ![]() :
: ![]() :
: ![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]() . R: a
. R: a
R.83 K ![]() deschis
deschis ![]() ; K
; K ![]() inchis C1 si C2 se incarca pana
ajunge la echilibru electrostatic. U1 = U2 = U: q1
= C1U; q2 = C2U; qo = (C1 + C2)U. In acest
moment U2 = 0
inchis C1 si C2 se incarca pana
ajunge la echilibru electrostatic. U1 = U2 = U: q1
= C1U; q2 = C2U; qo = (C1 + C2)U. In acest
moment U2 = 0 ![]() i2 = Imax.
i2 = Imax. ![]()
![]()
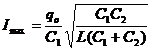 . R: a
. R: a
R.84. ![]()
![]()
![]()
![]()
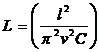
![]() L = 296 H. R: a
L = 296 H. R: a
R.85. ![]()
![]()
![]() . R: a
. R: a
R.85 . ![]() :
: ![]() ;
; ![]()
![]()
![]()
![]()
![]() . R: a
. R: a