|
|
|
Exista semnale cauzale foarte simple utilizate in analiza SLCI. Deseori, aceasta analiza este bazata pe determinarea raspunsului sistemului la un semnal de intrare dat. Proprietatea de superpozitie ne permite sa determinam raspunsul sistemului la un semnal de intrare oarecare prin suprapunerea raspunsurilor la semnale mai simple. De aici si interesul pentru determinarea raspunsurilor unui sistem dat la semnale foarte simple, numite semnale canonice.
Impuls unitar (sau impuls Dirac) d(t):
Reprezinta limita cand 
a unui impuls de
durata D si amplitudine 
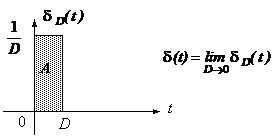
Aria A este intotdeauna egala cu unitatea indiferent de valoarea lui D. Se poate remarca un oarecare 'abuz' matematic in definirea impulsului d(t), care nu poate fi evitat decat utilizand teoria distributiei. Aceasta dificultate matematica reprezinta reflectarea faptului ca impulsul Dirac nu este un semnal fizic realizabil din cauza fronturilor crescatoare si descrescatoare de durata nula. Totusi, in automatica, se utilizeaza semnale care aproximeaza impulsul unitar.
Iesirea w(t) a unui sistem relaxat excitat cu un impuls unitar se numeste raspuns impulsional.
Treapta unitara (sau treapta Heaviside): g(t)
Numim raspuns indicial h(t) raspunsul la o treapta unitara a unui sistem unitar
Sa remarcam legatura intre impulsul unitar si treapta unitara:
,
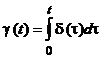si deci, cum sistemul este linear, vom obtine:
.
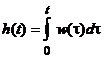Daca cunoastem raspunsul impulsional w(t) al unui SLCI, raspunsul indicial poate fi obtinut prin integrarea lui w(t).
Rampa unitara: t.g(t)
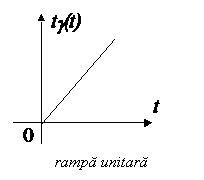
Este o rampa de panta 1, pentru care remarcam ca:
(2.13)
Tinand cont de ecuatia (2.13), raspunsul unui SLCI la o rampa unitara poate fi exprimat in functie de raspunsul indicial prin:
.
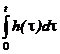Parabola
unitara :
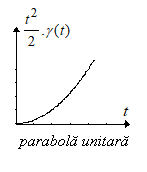
Legatura intre treapta unitara si parabola unitara este data de:
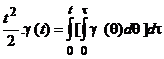(2.14)
Tinand cont de ecuatia (2.14), raspunsul unui SLCI la o parabola unitara poate fi exprimat in functie de raspunsul indicial:
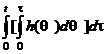
Un semnal canonic foarte important in automatica este semnalul sinusoidal, care reprezinta baza analizei frecventiale unui SLCI si care va face obiectul capitolului 5.
