|
|
|
Potentialul electric
Pentru simplificarea unor modele ale campului electric si -in special- pentru efectuarea mai usoara a unor aplicatii practice (in tehnica) ale fenomenelor electromagnetice, in teoria macroscopica a campului electromagnetic s-a introdus o marime derivata denumita potentialul electric rezervata descrierii locale a starii electrice a campului electromagnetic.
Potentialul electric reprezinta un camp scalar, cu valori in functie de punctul P din domeniul W de existenta, notate cu V(P), si definite prin expresia:
(1.38) 
sau mai simplu:
(1.38') 
in care: V(P0)sV0 este
potentialul electric al unui punct de referinta P0IΩ sau potentialul electric de
referinta (in cele mai multe aplicatii se considera V0=0); G este un traseu finit din campul Ω, ce contine
punctele P si P0; P este orice punct din campul Ω caruia se doreste a
i se atasa, cu relatia (1.38), o valoare scalara V(P)=V,
denumita potentialul electric
al punctului P; 
este integrala curbilinie (v.§9.1.2) efectuata in lungul
curbei G; Ē este intensitatea campului electric in puncte situate pe
"parcursul" G; 
este elementul de
curba orientat (v.§9.1.2) luat de-a lungul lui G si 
sunt produsele scalare
ale vectorilor 
si Ē din
punctele lui dl (v.fig.9.7).
Derivand in raport cu directia fiecare membru al
definitiei (1.38) rezulta (stiind ca 
), in acest caz local:
(1.39)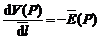 
sau (mai simplu) 
unde 
reprezinta
derivata unei functii scalare in raport cu o directie (v.§9.1.2
si fig.9.6). In teoria matematica a campului, conform celor
aratate in paragraful 9.1.2., derivata din relatia (1.39) se scrie
si sub forma 
, unde 
este versorul
directiei dupa care se efectueaza derivata in punctul PIΩ considerat, iar este operatorul diferential - vectorial "nabla" (se
reaminteste ca in coordonate carteziene 
). Pe de alta parte, 
adica derivata potentialului electric scalar
dupa o directie normala (
) la o suprafata echipotentiala ΣV (v.§ 9.1.2) reprezinta
valoarea gradientului potentialului electric (orientat dupa versorul
normalei n0 la
suprafata echipotentiala).
Din relatia (1.39) si cele prezentate anterior rezulta:
(1.40) 
si 
,
prin urmare, intr-un camp electromagnetic a carui stare locala este descrisa simultan de campul scalar al potentialelor electrice V si campul vectorial al intensitatilor campului electric Ē exista urmatoarea relatie:
(1.41) 
considerata ca o definitie locala (de punct) a potentialului electric V (ca marime derivata) in functie de intensitatea campului electric Ē (ca marime primitiva).
Relatiile (1.39) si (1.41) justifica afirmatia ca intensitatea campului electric deriva din potentialul electric sau, mai pe scurt: campul electric deriva dintr-un potential, ceea ce a impus si folosirea marimii derivate "potential electric" pentru descrierea locala a starii electrice a campului electromagnetic.
Definitia 
arata ca
vectorul camp electric 
, reprezinta
directia si sensul dupa care variaza (creste) cel mai
mult potentialul electric pornind dintr-un punct al campului. Conform
relatiei (1.40), directia vectorului grad V, adica directia lui Ē,
este normala pe suprafetele echipotentiale ΣV = adica pe suprafetele din campul Ω ale
caror puncte au toate acelasi potential electric. Sensul lui Ē, care conform relatiei
(1.41) este contrar variatiei locale a lui V (caci 
), este catre potentialele electrice
descrescatoare, iar valoarea absoluta |Ē| este direct proportionala cu viteza de
variatie dupa o directie data 
a lui V, conform
relatiei (1.39), adica depinde de derivata | V
Unitatea de
masura S.I. a potentialului electric poarta denumirea de volt (la plural volti), are simbolul V si -conform
relatiei de definitie (1.38)- reprezinta potentialul unui
punct V(P) care -fata de potentialul de referinta V(P0)-
creste, pe directia dreptei P0-P, cu o unitate de masura a
intensitatii campului electric (1V/m), pe o unitate de
masura a lungimii (1m) luata pe directia 
.
Relatiile (1.38), (1.39) si (1.41) explica si denumirea unitatii de masura S.I. a intensitatii campului electric, de volt pe metru, aleasa in functie de denumirea unitatii de masura a potentialului electric, care este mult mai utilizat in practica. Aceleasi relatii, explica si ecuatiile dimensionale pe care le au marimile de stare locala a campului electric:
[V] = [E] [L], [E] = [V] [L]-1. (1.42)
