Polarizatia electrica

Polarizatia electrica

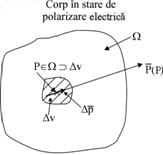
Se constata, experimental, ca si corpurile dielectrice mari (masive) se polarizeaza in toata masa lor. Atunci, inductiv, pentru a descrie local (in fiecare punct P al corpului dielectric polarizat ) starea lui de polarizare electrica s-a introdus un vector caruia i s-a dat numele de polarizatie electrica, care este o marime derivata si definita ca densitatea de volum a momentului electric (fig. 1.7):

, (1.14)

in general scriindu-se, in : .

Asa cum se precizeaza in manualul Preda, M., Cristea, P. si Spinei, F. (1980), "Introducerea acestei marimi se bazeaza pe ideea descompunerii unui corp intr-o reuniune de corpuri de dimensiuni foarte mici. Fiecare corp component, de volum , are un moment electric (fig. 1.7). Operatia de trecere la limita (1.14) este in acest caz numai teoretica si nu poate reprezenta un fapt experimental, deoarece componenta temporara a momentului electric al fiecarui corp component depinde de campul electric produs in corpul respectiv de ansamblul tuturor corpurilor componente si nu este deci masurabila individual. Polarizatia electrica descrie, deci, starea de polarizare locala a unui corp masiv, in conditii date, fiind ca marime derivata un exemplu tipic de marime introdusa inductiv pe plan teoretic ".

Corespunzator fenomenelor de polarizare temporara si de polarizare permanenta, avandu-se in vedere relatiile (1.12) si (1.14) se pot introduce si notiunile:

- polarizatia electrica permanenta

- polarizatia electrica temporara , astfel ca polarizatia electrica totala dintr-un punct al unui dielectric este:

(1.15)                           .

Unitatea de masura SI a polarizatiei electrice este coulomb pe metru la patrat, cu simbolul C/m² care rezulta din expresiile (1.11) si (1.14). Dimensiunea polarizatiei electrice rezulta din aceleasi relatii si este:

(1.16)                   .

Fluxul (v. § 9.1.2) vectorului are o semnificatie aparte. Pentru a vedea acest lucru, se poate porni de la relatia:

,

care rezulta din definitia (1.14) si inlocuindu-se cu , ce reiese din definitia (1.11), se mai poate scrie:

P

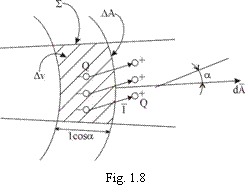Aceasta ultima relatie se refera la un "mic" volum dintr-un corp (fig.1.8).

Pentru acest volum, cu sectiunea si lungimea , se observa ca reprezinta sarcini dipolare de un semn continute in volumul . Deoarece volumul poate fi exprimat prin:

,

rezulta:

P ,

sau, la limita:

(1.17) .

Prin urmare, fluxul elementar al vectorului polarizatiei electrice reprezinta o sarcina electrica rezultata din sarcina dipolara a dipolilor electrici ce traverseaza partial suprafata (la limita dA), careia i se da numele de sarcina de polarizatie (notata adesea si cu ) de pe suprafata A, daca = const. (iar daca nu, la limita, de pe suprafata elementara ). Pentru o suprafata inchisa luata intr-un corp polarizat electric (v. fig. 1.8) se va putea scrie:

,

care reprezinta sarcina dipolara continuta in interiorul suprafetei inchise datorita "fractiunii" de dipol electric ramas inauntrul lui (v. fig.1.8) si:

,

care reprezinta sarcina dipolara ce "iese" (mai bine zis a "fractiunii" celeilalte a dipolilor electrici care prin orientarea lor in campul electric ies in afara suprafetei ), deoarece ele trebuie sa fie egale si de semn contrar in conditiile modelului dipolului electric aratat in figura 1.6.

La un corp ce are polarizatie electrica uniforma, adica = const. in orice punct din , sa va putea scrie:

,

deoarece pe toata suprafata "iese" si "intra" acelasi numar de "jumatati" de dipoli electrici (conform definitiei 1.11), adica aceeasi sarcina dipolara.

Daca suprafata este situata in intregime in vid si corpul se afla complet in interiorul ei, va exista de asemenea egalitatea:

,

deoarece in vid . Daca insa corpul este polarizat electric neuniform si suprafata este luata in corp, atunci intr-o parte poate iesi o sarcina dipolara mai mare decat cea care intra in cealalta parte. Aceasta sarcina Q se numeste sarcina electrica de polarizatie. Daca acelasi corp polarizat electric are si o sarcina electrica q (ca aceea obtinuta prin frecare), atunci suma celor doua sarcini electrice, se numeste sarcina electrica libera (notata cu ):

. (1.18)

Ca si in cazul sarcinii electrice q, corpurile cu polarizare electrica pot fi caracterizate si prin densitatea de volum a sarcinii electrice de polarizatie:

,

de unde rezulta:

(1.18v)

si prin densitatea de suprafata a sarcinii de polarizatie :

. (1.18A)

Expresiile (1.4), (1.17) si (1.18) justifica afirmatia ca perechea de marimi -densitatea de volum a sarcinii electrice (v. definitia 1.4) si - polarizatia electrica determina complet starea locala (dintr-un punct) de electrizare a unui corp.