|
|
|
Potentialul chimic
Relatiile din §5 si §6 sunt valabile numai pentru sisteme inchise, in care masa componentelor ramane constanta.
Pentru o faza deschisa cu c
componente, ecuatiile variatiilor infinitezimale ale functiilor
termodinamice devin (daca lucrul mecanic elementare este dat de 
):
(XIV.42)
(XIV.43)
(XIV.44)
(XIV.45)
unde 
, potentialul chimic al componentului i din sistem, este
definit ca marimea partial molara a functiilor
termodinamice:
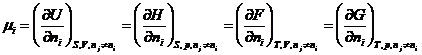(XIV.46)
Pentru un proces la presiune si temperatura constante:
(XIV.47)
si la echilibru:
(XIV.48)
Entalpia libera a unei faze este data de relatia:
(XIV.49)
Ecuatia de tip Gibbs-Duhem, la presiune si temperatura constante, este:
(la p si t constante) (XIV.50)
Relatiile aplicate lui μ sunt de forma identica cu cele cunoscute pentru entalpia libera.
Deoarece G = H - TS, conform expresiilor cunoscute pentru H si S (ecuatia (XIV.7)), in cazul unui amestec de gaze perfecte, se obtine:
si astfel
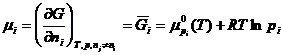(XIV.51)
Deoarece 
si 
, se obtin imediat expresiile:
(XIV.52)
(XIV.53)
Potentialul chimic pentru un component al unei solutii ideale lichide este dat de relatia:
In aceste ecuatii μ0 corespunde potentialului chimic standard (v. Cap. XIV si XIX).
Exemplul 17. O solutie ideala prezinta trei proprietati caracteristice: aditivitatea volumelor, termoneutralitatea (caldura de diluare este 0) si conformarea cu legea lui Raoult (prin generalizare, presiunea de vapori a unui component din solutie este egala cu produsul dintre fractia molara si presiunea de vapori a lichidului pur).
Sa se arate ca aceste trei proprietati decurg, in mod necesar, din ecuatia potentialului chimic de forma:
Rezolvare:
Conform ecuatiei cunoscute (XIV.13), se obtine:
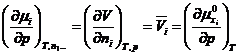
de unde rezulta ca, la temperatura si presiune
constante, volumul partial molar 
este o constanta,
independenta de compozitia solutiei, deci volumul solutiei
se poate calcula din suma volumelor componentelor.
A doua proprietate rezulta din ecuatia (XIV.37):
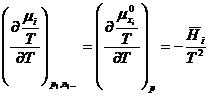
si deci, la temperatura si presiune constante, entalpia
partial molara 
este o constanta,
deoarece nu depinde de compozitie (caldura de diluare este
nula).
Legea lui Raoult (generalizata) rezulta din ecuatia de echilibru dintre vapori si solutie:
La temperatura si presiune
constante pi = const · xi si deoarece 
, 
(presiunea de vapori a
componentului pur), se obtine:
Exemplul 18. Sa se calculeze ΔG, ΔH si ΔS la formarea unui amestec dintr-un 1 mol O2 cu 1 mol N2 la presiune si temperatura constante, daca fiecare gaz se afla, inainte de amestec, la 25 oC si presiunea de 1 atm.
Rezolvare:
Utilizand, pentru fiecare gaz, ecuatia
potentialului chimic 
se obtine (i = 1
sau 2):
Rezulta, pentru amestec:
Deoarece, pentru gaze perfecte 
, rezulta:
Problema se rezolva si utilizand
ecuatiile 
si 
, unde .
Exemplul 19. Sa se calculeze lucrul minim de separare WS in componente pure a 1000 g solutie 18% de glucoza in apa, la 100 oC (la aceeasi presiune).
Rezolvare:
Entalpia libera a solutiei este
data de ecuatia 
(indicii 1 si 2
se refera la apa, respectiv glucoza).
Considerand solutia ideala,variatia de entalpie libera de amestec este:
si lucrul maxim de amestec este definit prin ecuatia:
iar lucrul minim de separare, prin ecuatia:
(a)
Solutia contine:
si 
iar fractiile molare sunt:
si 
Inlocuind valorile numerice in ecuatia (a), se obtine pentru lucrul de separare:
