Asociatii de oglinzi si lentile

Asociatii de oglinzi si lentile

1. O oglinda cu distanta focala f_O este alipita de o lentila subtire cu distanta focala f_L. Aratati ca sistemul optic este echivalent cu o oglinda si calculati distanta focala a acesteia.

Rezolvare. Consideram un obiect luminos plasat in fata sistemului optic. Lentila, care este traversata prima de catre lumina, da o imagine a acestuia care este preluata de oglinda pe post de obiect. Imaginea data de oglinda devine obiect nou pentru lentila care va da imaginea finala. Astfel lentila este strabatuta de lumina in ambele sensuri.

Aplicam prima formula a lentilelor, respectiv, oglinzilor in fiecare caz :

,

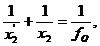
unde x₂ si x₂^’ sunt distantele pana la imaginile intermediare, iar in ultima ecuatie am luat celalalt focar al lentilei (_f_L) deoarece razele de lumina o traverseaza a doua oara de la dreapta la stanga, iar axa 0X am pastrat-o aceeasi.

Inmultind prima ecuatie cu -1 si adunandu-le membru cu membru obtinem :

= (1)

Ecuatia (1) este tipica pentru oglinzi sferice, unde in membrul drept trebuie sa fie inversul distantei focale a oglinzii echivalente.

Daca oglinda alipita lentilei este plana (f_O ) din ecuatia (1) rezulta :

sau : F_O=.

Pentru o lentila plan-convexa (f_L>0) obtinem o oglinda echivalenta concava, iar pentru o lentila plan-concava (f_L<0) obtinem o oglinda echivalenta convexa.

2. O musca aflata pe tavanul unei incaperi se deplaseaza cu vitaza constanta . Pe podeaua aflata la distanta d este o oglinda plana peste care este asezata o lentila subtire plan-convexa cu distanta focala f, f<, ca in figura 1. Calculati viteza imaginii mustei atunci cand musca ajunge pe axul optic principal al lentilei.

(musca)

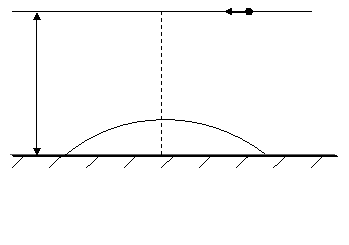
d

L

O

Fig. 1.

Rezolvare. Sistemul optic este echivalent cu o oglinda concava (vezi problema 1) cu

distanta focala F_O=. In aceste conditii se construieste grafic imaginea mustei ca in fig.2.

y₁

M₁ M (musca)

-y₂

C

-x₁ (imaginea) M^’

M^’₁

F

-x₂

y

x

Fig.2.

In timp ce musca se deplaseaza din M in M^’, cu viteza v, imaginea ei se deplaseaza transversal din M’ in M^’₁ cu viteza u. Deoarece v=, viteza transversala se modifica in acelasi raport ca si coordonata transversala y :

sau : u= v

In cazul oglinzii din fig. 2 :

Inlocuind datele problemei, F_O= x₁=, rezulta :

u=.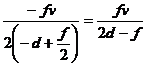

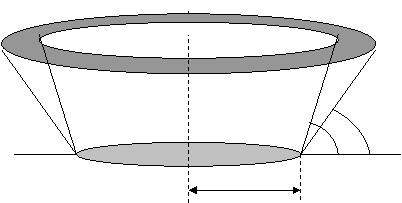
3. O oglinda plana de forma circulara avand raza R, are regiunea I in care un obiect liniar, paralel cu ea se vede in intregime si regiunea II in care obiectul se vede partial, ca in fig. 3. Determinati distanta la care se gaseste obiectul, lungimea acestuia si construiti grafic imaginea.

Rezolvare. In figura 4 se arata modul in care se construieste grafic obiectul AB, tinand cont de cele doua regiuni de vizibilitate, cat si imaginea acestuia in oglinda . Pentru ca obiectul sa fie vizibil in totalitate trebuie ca lumina ce pleaca din extremitatea lui, notata cu B, sa ajunga , prin reflexie pe oglinda, la observatorul plasat la limita regiunii I, in O^’₁. Analog, lumina ce pleaca din extremitatea opusa, notata A, trebuie sa ajunga la observator atunci cand acesta este plasat la extremitatea regiunii II, in punctul O^’₂, din fig.4. Astfel lungimea obiectului este AB atunci cand acesta este plasat la distanta h de oglinda

I Iiiiii iiiiiii

R

Fig.3

Se vede obiectul intreg Se vede Nu se vede

obiectul obiectul

A O B C O^’₁ partial O^’₂

h

O₁ O^’ O₂

A^’ B^’

R

Fig.4

In triungiul dreptunghic BCO₂: tg(90^°-α)= (1)

In triunghiul dreptunghic ACO₂: tg(90^°-β)= (2)

Dar: tg(90^°-α)= si analog: tg(90^°-β)=

Din (1) rezulta: BC=, iar din fig.4 se vede ca: OB=R-BC=R-

Din (2) rezulta: =, din care:

h= si : AB=2OB=2R