Radiatia termica

Radiatia termica

Radiatia termica este o radiatie de natura electromagnetica emisa de orice corp aflat la o temperatura oarecare T>0 K. Originea acestei radiatii este agitatia termica a particulelor corpului considerat.

1. Teoria clasica

Se poate arata, din considerente termodinamice, ca la echilibru, in interiorul unei cavitati cu peretii aflati la temperatura T se stabileste o radiatie de echilibru a carei densitate spectrala este (T), constanta in tot volumul incintei. Introducand puterea spectrala de emisie r(, T), ce reprezinta energia emisa de unitatea de arie a peretilor in unitatea de timp si cu frecvente in intervalul [ ;  +d se poate scrie relatia:

Introducand si coeficientul de absorbtie spectrala a(T), ce reprezinta energia absorbita de unitatea de arie peretilor in unitatea de timp si cu frecvente in intervalul [ ;  +dKirchhoff a aratat ca, pentru radiatia termica, raportul:

depinde numai de frecventa si de temperatura, fiind independent de natura corpului.

Radiatia termica a unui corp aflat la o temperatura T>0 poate fi tratata ca radiatia termica a unui corp ideal, numit corp negru. Un corp negru este caracterizat de absorbtia completa a oricarei radiatii ce cade pe suprafata sa (deci a(T)=1).

Pentru un corp negru, pe baza principiilor termodinamicii s-a aratat ca:

(t, ) = ³ f( /T)

sau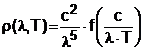                         

In cadrul fizicii clasice pentru functia f nu a putut fi gasita o expresie analitica, dar s-a putut demonstra ca ( T), prezinta un maxim ce se deplaseaza spre valori mai mari de frecventa odata cu cresterea temperaturii. Din conditia de maxim se poate obtine relatia:

(3.1)

expresie ce poarta numele de legea de deplasare a lui Wien.

Tot in cadrul fizicii clasice s-a obtinut legea Stefan - Boltzmann:

(3.2)

in care R este radianta si  este constanta Stefan Boltzmann, valoarea ei neputand fi obtinuta pe cale analitica. Legea arata ca energia totala a radiatiei emise de unitatea de arie a corpului negru, in unitatea de timp, este proportionala cu T⁴.

S-au incercat diferite forme pentru functia ( T) dintre care una propusa de Wien:

(3.3)

unde C este o constanta ce se determina din datele experimentale, iar k_B este constanta lui Boltzmann. Se constata ca legea este valabila pentru frecvente mari (fig. 3.1).

Pornind de la studii de electrodinamica clasica, considerand atomii cavitatii ca oscilatori, ce emit si primesc radiatia din interiorul cavitatii, se obtine o relatie de tipul:

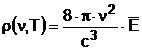(3.4)

unde  este energia medie a atomilor din peretii incintei. Considerand oscilatorii liniari, pe baza teoremei echipartitiei energiei pe grade de libertate se obtine:

(3.5)

si deci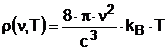                    

relatie ce poarta numele de formula Rayleigh - Jeans. Relatia nu prevede scaderea lui ( T) la frecvente mari, dar da rezultate bune la frecvente mici (fig 3.1).

Fig. 3.1

2. Formula lui Planck

Planck considera ca relatia (3.4) din paragraful precedent este corecta dar asimileaza atomii peretilor cavitatii cu niste oscilatori armonici de frecvente diferite si de energii cuantificate, proportionale cu frecventele: E_n=n h , unde n este un intreg, iar h constanta lui Planck cu valoarea h = 6,626x10^-34 J s. Deci schimbul de energie intre radiatie si materie se face prin cuante numite fotoni de energie h. Energia medie a unui oscilator de frecventa  este obtinuta pornind de la distributia Boltzmann:

(3.6)

Substituind (3.6) in (3.4) se obtine:

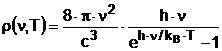(3.7)

Formula lui Planck este in concordanta cu datele experimentale, iar relatiile lui Wien si respectiv Rayleigh - Jeans se obtin din aceasta drept cazuri particulare valabile pentru limitele frecventelor mari si respectiv mici.

Introducerea cuantelor de energie a avut o importanta deosebita pentru dezvoltarea fizicii, fiind primul din conceptele de baza ale noii fizici care era pe cale sa se nasca. Constanta h este o constanta universala, fiind prima constanta universala introdusa in studiul fizicii.