
|
|
|
Legea circuitului magnetic
Aceasta lege stabileste sub aspect cantitativ efectul magnetic al campului electric (variabil in timp) si al corpurilor aflate in stare electrocinetica. In Fizica ea este denumita adesea "legea inductiei magnetoelectrice ", insa denumirea uzuala de "lege a circuitului magnetic" se datoreaza aplicatiei pe care il are modelul acestei legi in practica, la calculul circuitelor magnetice (v.cap.6).
Experienta arata ca in jurul corpurilor
conductoare aflate in regim electrocinetic, caracterizate de
intensitatile curentilor de conductie i, se produce un camp magnetic atata timp cat ![]() , acest fenomen reprezentand efectul magnetic al
electrocineticii. Tot experienta arata ca daca printr-o
suprafata oarecare deschisa exista un flux electric
, acest fenomen reprezentand efectul magnetic al
electrocineticii. Tot experienta arata ca daca printr-o
suprafata oarecare deschisa exista un flux electric ![]() variabil in timp se
produce un camp magnetic, a carui intensitate in punctele de pe conturul
ce margineste suprafata depind de viteza de variatie a
fluxului electric, astfel ca daca
variabil in timp se
produce un camp magnetic, a carui intensitate in punctele de pe conturul
ce margineste suprafata depind de viteza de variatie a
fluxului electric, astfel ca daca ![]() campul magnetic dispare. Aceste fapte reprezinta
aspectul fenomenologic-calitativ, al efectului magnetic al campului electric
si electrocinetic.
campul magnetic dispare. Aceste fapte reprezinta
aspectul fenomenologic-calitativ, al efectului magnetic al campului electric
si electrocinetic.
Legea circuitului magnetic stabileste pe cale
experimentala, fie printr-un model la
scara globala
(integral), fie prin unul local (de punct), legatura cantitativa
dintre marimile de stare: intensitate a campului magnetic![]() -pe de o parte- si intensitatea curentului de
conductie i (eventual densitatea de curent
-pe de o parte- si intensitatea curentului de
conductie i (eventual densitatea de curent ![]() ) si fluxul electric
) si fluxul electric ![]() (eventual
inductia electrica
(eventual
inductia electrica ![]() ) - pe de alta parte.
) - pe de alta parte.
Daca intru-un domeniu ![]() , de existenta a campului electromagnetic, se
considera un contur inchis oarecare
, de existenta a campului electromagnetic, se
considera un contur inchis oarecare ![]() si o
suprafata oarecare
si o
suprafata oarecare ![]() marginita de
acest contur
marginita de
acest contur ![]() , astfel incat conturul
, astfel incat conturul ![]() inlantuie
corpurile aflate in stare electrocinetica determinata de curenti
de conductie cu intensitatile
inlantuie
corpurile aflate in stare electrocinetica determinata de curenti
de conductie cu intensitatile ![]() si/sau prin
suprafata
si/sau prin
suprafata ![]() exista un flux
electric
exista un flux
electric ![]() variabil in timp cu viteza de variatie
variabil in timp cu viteza de variatie ![]() , atunci in fiecare punct
, atunci in fiecare punct ![]() va exista un camp
magnetic cu intensitatea
va exista un camp
magnetic cu intensitatea ![]() a carui circulatie pe conturul
a carui circulatie pe conturul ![]() , care reprezinta tensiunea magnetomotoare Fm, definita de
relatia (1.51), adica
, care reprezinta tensiunea magnetomotoare Fm, definita de
relatia (1.51), adica ![]() este egala cu
suma intensitatilor curentilor de conductie prin
suprafata
este egala cu
suma intensitatilor curentilor de conductie prin
suprafata ![]() , adica
, adica ![]() , plus viteza de variatie in timp a fluxului electric
, plus viteza de variatie in timp a fluxului electric ![]() prin suprafata
prin suprafata ![]() , adica
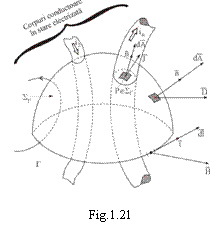
, adica ![]() (fig.1.21).
(fig.1.21).
Aceasta formulare narativa se poate inlocui cu modelul:
(1.83) ![]()
unde:
![]() - tensiunea
electromotoare (t.m.m.)
- tensiunea
electromotoare (t.m.m.) ![]()
![]()
in care ![]() este densitatea curentului de conductie determinata
in punctele
este densitatea curentului de conductie determinata
in punctele![]() de corpurile aflate in stare electrocinetica si:
de corpurile aflate in stare electrocinetica si:
(1.84) ![]() .
.
Modelul (1.83) care reprezinta formula
integrala (globala, relativa la conturul ![]() din camp) a legii
circuitului magnetic se poate scrie, tinand seama de expresiile
precedente, si in formlele:
din camp) a legii
circuitului magnetic se poate scrie, tinand seama de expresiile
precedente, si in formlele:
![]()
![]()
sau, mai simplu:
![]()
![]() ,
,
precum si:
![]()
![]()
Sensul elementului de arie orientat ![]() deci sensul normalei
deci sensul normalei ![]() la suprafata
la suprafata ![]() , este corelat cu sensul elementului de curba orientat
, este corelat cu sensul elementului de curba orientat ![]() , deci cu sensul tangentei
, deci cu sensul tangentei ![]() la curba
la curba ![]() dupa regula
sistemului drept (regula "burghiului drept"), conform schitei din figura
1.21.
dupa regula
sistemului drept (regula "burghiului drept"), conform schitei din figura
1.21.
In cazul corpurilor in miscare, conturul ![]() si suprafata
si suprafata
![]() marginita de
acest contur, trebuie atasate corpurilor si antrenate cu viteza
marginita de
acest contur, trebuie atasate corpurilor si antrenate cu viteza ![]() de deplasarea
corpurilor, ceea ce explica ca in modelul
de deplasarea
corpurilor, ceea ce explica ca in modelul ![]() s-a considerat derivata substantiala
(materiala) df/dt a fluxului electric in raport cu timpul (v.§
9.1.2).
s-a considerat derivata substantiala
(materiala) df/dt a fluxului electric in raport cu timpul (v.§
9.1.2).
Termenii: ![]() din modelele
din modelele ![]() care reprezinta suma algebrica a
curentilor ce caracterizeaza
starea electrocinetica a conductorilor ce strabat suprafata
care reprezinta suma algebrica a
curentilor ce caracterizeaza
starea electrocinetica a conductorilor ce strabat suprafata ![]() , poarta denumirea de solenatie, care se
noteaza cu
, poarta denumirea de solenatie, care se
noteaza cu ![]() (sau in general cu
(sau in general cu ![]() ) si este in fapt o marime de stare
electrocinetica globala a corpurilor printr-o sectiune
totala
) si este in fapt o marime de stare
electrocinetica globala a corpurilor printr-o sectiune
totala ![]() , dusa prin corpuri dar marginita pe conturul
, dusa prin corpuri dar marginita pe conturul ![]() (v.fig.1.21). In suma
(v.fig.1.21). In suma ![]() , curenti au sensul + sau - dupa cum rezulta
din asocierea lor cu semnul lui
, curenti au sensul + sau - dupa cum rezulta
din asocierea lor cu semnul lui ![]() de pe conturul
de pe conturul ![]() conform regulii
burghiului drept (astfel, pentru figura 1.21, solenatia este
conform regulii
burghiului drept (astfel, pentru figura 1.21, solenatia este ![]() ).
).
Relatia (1.84), a derivatei substantiale a fluxului magnetic in raport cu timpul, are dimensiunile unui curent, caci:
![]() (1.85)
(1.85)
caci, in conformitate cu legea fluxului electric ![]() si ecuatia
dimensionala (1.35)
si ecuatia
dimensionala (1.35)![]() si in conformitate cu legea conservarii sarcinii
electrice, prezentata in paragraful ce urma (v.§.1.3.9), asa cum
rezulta din modelul (1.91), termenul dimensional
si in conformitate cu legea conservarii sarcinii
electrice, prezentata in paragraful ce urma (v.§.1.3.9), asa cum
rezulta din modelul (1.91), termenul dimensional ![]() are dimensiunea
are dimensiunea ![]() a curentului electric.
De aceea (precum si din alte motive ce vor fi aratate in subcapitolul
4.2), derivata fluxului electric prin suprafata
a curentului electric.
De aceea (precum si din alte motive ce vor fi aratate in subcapitolul
4.2), derivata fluxului electric prin suprafata ![]() este denumita intensitatea
curentului hertzian prin
este denumita intensitatea
curentului hertzian prin ![]() , notat cu
, notat cu ![]() , si definit prin:
, si definit prin:
![]() . (1.86)
. (1.86)
Transcriindu-se, dimensional legea circuitului magnetic
sub formula modelului ![]() , rezulta dimensiunea intensitatii campului
magnetic [H], precum si a t.m.m.
, rezulta dimensiunea intensitatii campului
magnetic [H], precum si a t.m.m.![]() sau tensiunii magnetice
sau tensiunii magnetice ![]()
![]() (1.87)
(1.87)
ceea ce explica si unitatea de masura SI aleasa pentru intensitatea campului magnetic, de amper pe metru (A/m).
Plecand de la formula integrala ![]() a acestei legi in care
membrul din stanga poate fi scris conform teoremei lui Stokes (9.28) ca flux al
rotorului campului magnetic
a acestei legi in care
membrul din stanga poate fi scris conform teoremei lui Stokes (9.28) ca flux al
rotorului campului magnetic ![]() prin suprafata
prin suprafata ![]() , adica:
, adica:
![]()
iar termenul din membrul drept, al derivatei substantiale a fluxului electric in raport cu timpul cu dezvoltarea (9.44), adica:
![]()
rezulta ca legea ![]() devine:
devine:
![]() ,
, ![]()
care este o noua
forma de exprimare integrala (global, relativ la orice
suprafata ![]() ) a legii circuitului magnetic. Dimensiunile tuturor
termenilor din membrul drept este aceea de curent electric si ei au fost
denumiti, in ordine:
) a legii circuitului magnetic. Dimensiunile tuturor
termenilor din membrul drept este aceea de curent electric si ei au fost
denumiti, in ordine:
![]() - intensitatea curentului de conductieprin
suprafata
- intensitatea curentului de conductieprin
suprafata ![]() ,
,
![]() - curentul de deplasare
prin suprafata
- curentul de deplasare
prin suprafata ![]() ,
,
![]() - curent de
convectie prin suprafata
- curent de
convectie prin suprafata ![]() ,
,
deoarece conform legii fluxului electric (1.66) ![]() ;
;
![]() - curentul Roentgen teoretic,
- curentul Roentgen teoretic,
![]() fiind viteza unui corp
dielectric ce contine conturul
fiind viteza unui corp
dielectric ce contine conturul ![]() , care in teoria macroscopica clasica a campului
electromagnetic nu poate fi justificat si evidentiat experimental,
efectul acestui termen fiin practic neglijabil[1].
, care in teoria macroscopica clasica a campului
electromagnetic nu poate fi justificat si evidentiat experimental,
efectul acestui termen fiin practic neglijabil[1].
Cu aceste notatii, legea circuitului magnetic are si un alt model integral si anume:
(1.83V) ![]() cu
cu ![]() .
.
Asupra curentilor care intervin in aceasta relatie se va reveni pe larg in subcapitolul 4.2.
In domeniile de continuitate, forma locala a legii circuitului magnetic se
obtine imediat din forma integrala (1.83V),
stiindu-se ca suprafata ![]() este arbitrara
(oricare din camp), fiind:
este arbitrara
(oricare din camp), fiind:
(1.88) ![]() ,
,
in care ![]() este densitatea de
volum a sarcinii electrice din punctul
este densitatea de
volum a sarcinii electrice din punctul ![]() si
si ![]() sunt vectorii de stare
din acelasi punct P, iar
sunt vectorii de stare
din acelasi punct P, iar ![]() este viteza pe care o
are un corp in puctul P, unde
exista densitatea
este viteza pe care o
are un corp in puctul P, unde
exista densitatea ![]() .
.
Deoarece,
dupa cum se va vedea si in subcapitolul 4.2, ultimii trei termeni din
membrul drept reprezinta densitati de curent (ca si ![]() care este densitatea
curentului de conductie) si anume:
care este densitatea
curentului de conductie) si anume: ![]() -densitatea (de
suprafata) a curentului de deplasare,
-densitatea (de
suprafata) a curentului de deplasare, ![]() - densitatea curentului de convectie si rot
- densitatea curentului de convectie si rot![]() - densitatea curentului Roentgen teoretic, atunci legea
locala a circuitului magnetic mai are o forma si anume:
- densitatea curentului Roentgen teoretic, atunci legea
locala a circuitului magnetic mai are o forma si anume:
![]() rot
rot ![]()
care dimensional se verifica
prin ![]() sau
sau ![]()
Daca
in camp nu sunt corpuri mobile (deci ![]() ), atunci legea circuitului magnetic locala, in medii
continue, devine:
), atunci legea circuitului magnetic locala, in medii
continue, devine:
![]() rot
rot
![]()
forma foarte
frecventa in practica, ca si ![]() (cand
(cand ![]() ).
).
In cazul unor suprafete de
discontinuitate ![]() din campul W, se considera ca si in figura 1.20, un contur
inchis foarte mic dreptunghiular
din campul W, se considera ca si in figura 1.20, un contur
inchis foarte mic dreptunghiular ![]() cu
cu ![]() ce delimiteaza o
suprafata foarte mica
ce delimiteaza o
suprafata foarte mica ![]() Daca
Daca ![]() atunci
atunci ![]() si in punctul
si in punctul ![]() catre care se
restrange (la limita)
catre care se
restrange (la limita) ![]() rezulta:
rezulta:
![]()
adica:
![]() ,
,
sau, deoarece la limita, ![]() si
si ![]() , iar
, iar ![]()
![]() unde versorii
tangentelor la
unde versorii
tangentelor la ![]() pe
pe ![]() si
si ![]() sunt
sunt ![]() relatia
precedenta devine:
relatia
precedenta devine:
![]()
![]()
de unde rezulta:
![]()
sau:
![]() (1.89)
(1.89)
care modeleaza faptul
ca in campul magnetic, in punctele
unei suprafetede discontinuitate componentele tangentiale Ht
ale intensitatii campului magnetic se conserva la trecerea
dintr-un mediu in altul prin suprafata de discontinuitate. Aceasta,
impreuna cu faptul ca pe ![]() componentele normale Bn ale inductiei
magnetice se conserva -conform relatiei (1.70)- arata ca la
trecerea printr-o suprefata de discontinuitate liniile de camp
magnetic se refracta.
componentele normale Bn ale inductiei
magnetice se conserva -conform relatiei (1.70)- arata ca la
trecerea printr-o suprefata de discontinuitate liniile de camp
magnetic se refracta.
[1]Experientele
efectuate de fizicianul german Roentgen [Wilhelm Conrad Röntgen, 1845-1923],
care a studiat in special fenomenul descarcarilor electrice in gaze,
au aratat ca expresia curentului iR,
care ar putea justifica efectele magnetice ale variatiei in timp a
fluxului electric, ar trebui sa fie ![]() ceea ce nu
rezulta din dezvoltarea derivatei
ceea ce nu
rezulta din dezvoltarea derivatei ![]() .
.