
|
|
|
Efectul Joule-Thomson
 La destinderea in vid (fara
efectuare de lucru mecanic exterior) energia interna U a gazului ideal
(perfect) Ši deci temperatura lui ramane neschimbata:
La destinderea in vid (fara
efectuare de lucru mecanic exterior) energia interna U a gazului ideal
(perfect) Ši deci temperatura lui ramane neschimbata: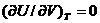 . In practica, insa, gazele reale se comporta diferit, adica
la o destindere adiabatica in vid (fara lucru mecanic exterior) gazul se
raceŠte iar la o comprimare, fara lucru mecanic exterior, gazul se incalzeŠte
(exemplu cazul umflarii cauciucului unui automobil de la un rezervor de
presiune. La umflarea cu o pompa de mana incalzirea se datoreaza, in parte,
comprimarii adiabatice cu lucru mecanic.
. In practica, insa, gazele reale se comporta diferit, adica
la o destindere adiabatica in vid (fara lucru mecanic exterior) gazul se
raceŠte iar la o comprimare, fara lucru mecanic exterior, gazul se incalzeŠte
(exemplu cazul umflarii cauciucului unui automobil de la un rezervor de
presiune. La umflarea cu o pompa de mana incalzirea se datoreaza, in parte,
comprimarii adiabatice cu lucru mecanic.
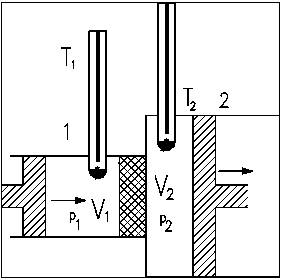
Acest fenomen a fost studiat in laborator de catre Joule Ši Thomson cu ajutorul dispozitivului din figura alaturata. In acest dispozitiv gazul a fost lasat sa se destinda de la presiunea constanta p1 la presiunea constanta p2, scurgandu-se laminar printr-un perete poros. Pentru menainerea constanta a presiunilor se deplaseaza cele doua pistoane in mod corespunzator: pistonul 1 se apropie iar pistonul 2 se indeparteaza de peretele poros. Rolul peretelui poros (un simplu tampon de vata) este numai acela de a asigura o curgere laminara fara turbulenae. Cele doua termometre indica temperaturile in cele doua compartimente. Cilindrii sunt confecaionaai dintr-un material termoizolant, pentru ca procesul sa fie adiabatic.
Se constata ca cele mai multe gaze se racesc (T2 < T1) in cazul destinderii laminare. Sunt insa unele care se incalzesc (T2 > T1).
Variaaia temperaturii gazului in timpul destinderii laminare fara efectuare de lucru mecanic, se numeste efectul Joule-Thomson.
O masura
a efectului Joule-Thomson este coeficientul diferenaial ![]() , numit coeficient J-Th. Cu excepaia hidrogenului Ši a
heliului la temperatura obiŠnuita, pentru toate gazele d>0 adica gazele reale iŠi cresc temperatura cu creŠterea
presiunii. Explicaaia
este data de faptul ca la densitaai mai mari ale gazelor distanaele intre
molecule sunt mai mici Ši incep sa apara foraele de respingere intre molecule
(vezi diagrama foraei de interacaie Ši a energiei potenaiale dintre doua
molecule), Ši prin destinderea gazului aceste forae contribuie la creŠterea
energiei cinetice a moleculelor, adica a temperaturii gazului. Daca
se efectueaza experimentul Joule-Thomson la diferite temperaturi se constata
ca, la temperaturi suficient de scazute chiar Ši H2 Ši He au d pozitiv iar la temperaturi mai ridicate Ši pentru alte
gaze decat He Ši H2 d
devine negativ. Exista, deci, o anumita temperatura, care difera de la gaz la
gaz, la care d schimba semnul, numita temperatura de inversiune.
, numit coeficient J-Th. Cu excepaia hidrogenului Ši a
heliului la temperatura obiŠnuita, pentru toate gazele d>0 adica gazele reale iŠi cresc temperatura cu creŠterea
presiunii. Explicaaia
este data de faptul ca la densitaai mai mari ale gazelor distanaele intre
molecule sunt mai mici Ši incep sa apara foraele de respingere intre molecule
(vezi diagrama foraei de interacaie Ši a energiei potenaiale dintre doua
molecule), Ši prin destinderea gazului aceste forae contribuie la creŠterea
energiei cinetice a moleculelor, adica a temperaturii gazului. Daca
se efectueaza experimentul Joule-Thomson la diferite temperaturi se constata
ca, la temperaturi suficient de scazute chiar Ši H2 Ši He au d pozitiv iar la temperaturi mai ridicate Ši pentru alte
gaze decat He Ši H2 d
devine negativ. Exista, deci, o anumita temperatura, care difera de la gaz la
gaz, la care d schimba semnul, numita temperatura de inversiune.
In cursul destinderii laminare ramane constanta entalpia H a gazului Ši nu energia interna.
Conform
principiului I al termodinamicii pentru 1 mol de gaz ideal ce a trecut prin
peretele poros: ![]() Ši deoarece volumul
molului de gaz este V1 la p1 Ši V2 la p2
atunci:
Ši deoarece volumul
molului de gaz este V1 la p1 Ši V2 la p2
atunci:![]()
Calculul coeficientului J-Th Ši al temperaturii de inversiune.
Entalpia
H este o funcaie de p Ši T Ši diferenaiala ei totala este: 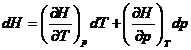
![]()
![]()
![]()
![]() Dar
in procesul J-Th dH=0 deci scriind
Dar
in procesul J-Th dH=0 deci scriind 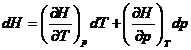 =0 se poate scoate:
=0 se poate scoate: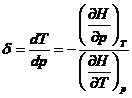 unde
unde ![]() iar
iar 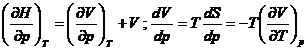 deci:
deci: 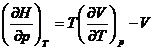 Ši atunci:
Ši atunci: 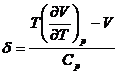
In aceasta formula Cp este cunoscut, ![]() coeficient de dilatare volumica a gazului Ši astfel, Štiind
pe V Ši pe T se poate calcula valoarea lui d.
Folosind pentru gazele reale ecuaaia lui Van der Waals pentru 1 mol Ši la
presiune nu prea mare:
coeficient de dilatare volumica a gazului Ši astfel, Štiind
pe V Ši pe T se poate calcula valoarea lui d.
Folosind pentru gazele reale ecuaaia lui Van der Waals pentru 1 mol Ši la
presiune nu prea mare: ![]() in care,
dezvoltand-o, neglijam
in care,
dezvoltand-o, neglijam ![]() iar pe V din
termenul 2 al corecaiei il inlocuim cu:
iar pe V din
termenul 2 al corecaiei il inlocuim cu: ![]() atunci ecuaaia
devine:
atunci ecuaaia
devine: ![]()
Prin
derivare in raport cu T rezulta ![]() adica coeficientul
de dilataaie.
adica coeficientul
de dilataaie.
![]()
![]()
![]() Pentru
a afla numaratorul in expresia lui d
inmulaim aceasta ecuaaie cu T Ši scadem din ea pe V (expresia de mai sus):
Pentru
a afla numaratorul in expresia lui d
inmulaim aceasta ecuaaie cu T Ši scadem din ea pe V (expresia de mai sus): ![]() , deci coeficientul J-Th devine:
, deci coeficientul J-Th devine:
![]()
![]()
In concluzie cu aceasta expresie se poate calcula coeficientul J-Th din constantele a Ši b ale ecuaaiei lui Van der Waals.
Temperatura de
inversiune Ti , se obaine
anuland pe d adica, anuland paranteza din
expresia lui, caci T nu poate fi nul![]()
Temperatura Boyle este temperatura la
care legile gazelor perfecte sunt aplicabile gazelor reale pana la presiuni mai
mari. Din calculul temperaturii Boyle s-a gasit ca ![]() de unde rezulta ca temperatura de inversiune este dublul
temperaturii Boyle Ti=2TB.
de unde rezulta ca temperatura de inversiune este dublul
temperaturii Boyle Ti=2TB.