Relatii matematice intre marimile termodinamice

Relatii matematice intre marimile termodinamice

In multe probleme de chimie fizica este necesara stabilirea relatiilor dintre diferitele marimi termodinamice. Stabilirea directa a acestor relatii este, in general, dificila. Este suficient sa se remarce ca, pentru cele opt marimi termodinamice (U, H, S, F, G, p, V, T), sunt posibile derivate partiale de ordinul intai si un numar mult mai mare de relatii intre ele.

Din aceasta cauza se recomanda utilizarea uneia din urmatoarele metode:

a) Metoda Bridgeman foloseste o tabela de expresii care permit determinarea derivatelor de ordinul intai in termeni de trei marimi masurabile experimental:

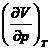, si

folosind relatia pur formala:

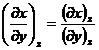(XIV.54)

unde x, y, z reprezinta trei din cele opt marimi termodinamice.

Exemplul 20. Sa se calculeze, prin metoda Bridgeman, coeficientul Joule-Thomson .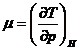

Rezolvare:

Din tabela XIV.1 se obtine:

de unde:

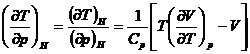
Tabela XIV.1 Tabela Bridgeman

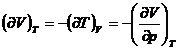
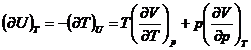
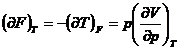
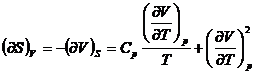
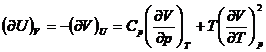
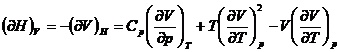
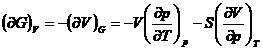
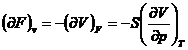
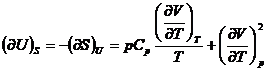
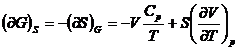
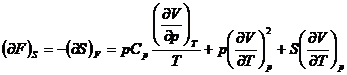
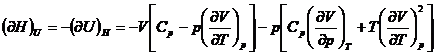
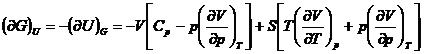
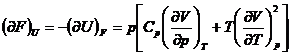
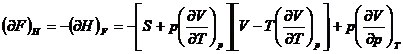
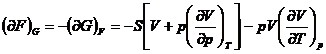
b) Metoda Shaw este un procedeu sistematic pentru determinarea relatiilor termodinamice si se bazeaza pe folosirea determinantilor functionali (iacobiani):

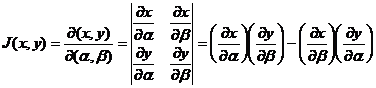       (XIV.55)

unde x, y sunt doua variabile dependente si sunt doua variabile independente.

Proprietatile importante ale iacibianului sunt:

(XIV.56)

(XIV.57)

(XIV.58)

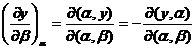(XIV.59)

Din ultimele doua ecuatii rezulta:

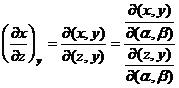(XIV.60)

O diferentiala totala:

dx = Mdy + Mdz

se poate scrie sub forma:

J(x,) = MJ(y,) + NJ(z,) (XIV.61)

Intr-adevar:

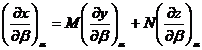
sau

Exemplul 21. Sa se calculeze prin metoda Shaw coeficientul Joule-Thomson .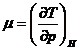

Rezolvare:

Potrivit ecuatiilor (XIV.58, XIV.59 si XIV.60) rezulta:

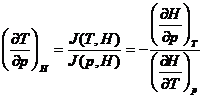
unde si

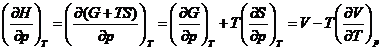
Prin urmare:

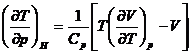
sau

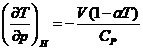
Exemplul 22. Sa se stabileasca expresia derivatei .

Rezolvare:

Considerand ca variabile independente p si T, se obtine:

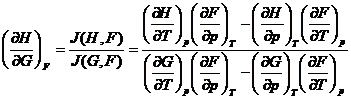
Din ecuatiile cunoscute sau usor de stabilit:

;

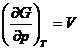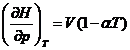(v. exemplul precedent)

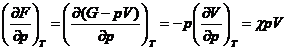
rezulta astfel:

La folosirea metodei Shaw, pentru comoditatea calculului, se recomanda folosirea tabelei XIV.2, in care intervin patru variabile independente p, V, T, S si determinantii functionali definiti prin relatiile:

a = J(V,T) = -J(T,V)

b = J(p,V) = -J(V,p)

c = J(p,S) = -J(S,p)

l = J(p,T) = -J(T,p)

n = J(V,S) = -J(S,V)

Intre a, b, c, l si n exista relatia:

(XIV.62)

Tabela XIV.2 Tabela Shaw

Exemplul 23. Sa se verifice ca J(T,S) = J(p,V).

Rezolvare:

Ecuatia se poate scrie sub forma evident verificata:

deoarece

(v. (XIV.38))

Exemplul 24. Sa se verifice ecuatiile 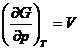si .

Rezolvare:

Conform ecuatiei (XIV.58) si cu ajutorul tabelei XIV.2, se obtine imediat:

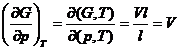
si

observand ca valorile iacobianului de la numarator, respectiv de la numitor, se gasesc la intersectia coloanei si randului respectiv.

Exemplul 25. Sa se calculeze expresia derivatei in termeni de marimi masurabile.

Rezolvare:

Conform ecuatiei (XIV.58) si a tabelei XIV.2, se obtine:

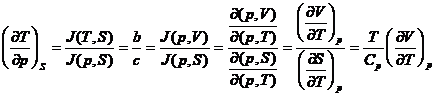
Exemplul 26. Sa se calculeze , alegand ca variabile independente p si T.

Rezolvare:

Se foloseste relatia:

si cu ajutorul tabelei XIV.2 se obtine:

Pentru a elimina pe n = J(V,S) se multiplica cu l si se tine seama de relatia (XIV.62):

Rezulta:

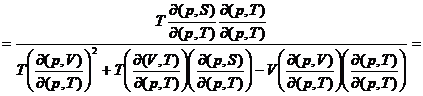
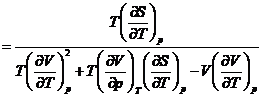
Deoarece 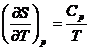, se obtine:

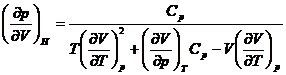
Pentru un gaz perfect:

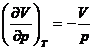, si

PROBLEME

1. Sa se utilizeze presiunea si volumul, respectiv entropia si temperatura, ca variabile independente pentru reprezentarea grafica a unui ciclu constituit din vaporizarea unui lichid la presiune constanta, o detenta adiabatica si vaporizare, o condensare izoterma si o comprimare adiabatica. Sa se calculeze lucrul si caldura in acest proces ciclic.

*2. Sa se stabileasca semnificatia fizica a subtangentei izobarei, respectiv izocorei, in diagrama T-S.

*3. Sa se indice cateva metode de calcul a temperaturii de zero absolut.

4. Caldura de ardere a metanului este -212,95 . Sa se indice cateva metode pentru obtinerea lucrului mecanic prin combustia acestui gaz si sa se compare randamentele diferitelor metode imaginate.

5. Sa se calculeze lucrul minim necesar pentru pulverizarea a 1 g apa, la 20 ^oC, in picaturi cu un diametru mediu de 100 mμ. (In acest caz, variatia de entalpie libera este egala cu variatia energiei superficiale).

6. Presupunand ca n₁ moli toluen si n₂ moli xilen se amesteca fara efect termic si fara variatie de volum, formand o solutie in care fractiile molare sunt x₁ si x₂, sa se calculeze ΔU, ΔH si ΔS si lucrul dat de procesul de amestecare.

7. La presiunea de 22,8 atm apa fierbe la 220 ^oC. Sa se calculeze fractiunea maxima din caldura absorbita la aceasta temperatura, care se transforma in lucru mecanic intr-o masina termica avand un cazan la 22,8 atm si un condensator la 45 ^oC.

8. Sa se calculeze lucrul mecanic minim necesar unei masini frigorifice care transporta o calorie de la 0 la 25 ^oC.

9. Sa se arate ca, pentru procesul de detenta in vid a unui gaz perfect, cresterea de entropie este mai mare decat cea calculata pe baza caldurii absorbite.

10. Sa se verifice ca procesul de amestecare a doua cantitati de apa de temperaturi diferite este insotit de o scadere a energiei libere a sistemului.

11. Pentru inlocuirea apei in masinile termice s-a propus bifenilul sau un amestec bifenil-bifenileter. Sa se analizeze avantajele si dezavantajele pe care le prezinta aceste substante fata de apa si mercur.

12. Sa se arate ca, pentru apa la 4 ^oC (densitate maxima), .

13. Sa se arate ca, daca doua faze ale unui sistem eterogen nu sunt la echilibru, o substanta tinde sa treaca din faza in care potentialul chimic respectiv este mai mare in faza in care potentialul chimic este mai mic.

14. Volumul unui mol de azot la 0 ^oC este 10 l (starea 1). In starea 2, aceeasi cantitate de azot ocupa 20 l la 100 ^oC. Intre cele doua stari sunt posibile o infinitate de transformari. Considerand urmatoarele doua transformari:

a) destindere izoterma la 0 ^oC si incalzire la 100 ^oC;

b) incalzire la volum constant de la 0 la 100 ^oC si destindere izoterma, sa se  compare valorile numerice ale marimilor ΔU, ΔH, W, Q, ΔS si sa se interpreteze rezultatele.

15. Sa se calculeze variatia de entropie pentru un mol gaz ideal, care trece de la 0 ^oC si 1 atm la 100 ^oC si 2,5 atm.

16. Capacitatea calorica molara a CO₂ la presiune constanta este:

Sa se calculeze variatia de entropie pentru procesul de racire a unui mol CO₂ la presiunea constanta, de la 100 la 0 ^oC. Utilizand acest rezultat, sa se calculeze capacitatea calorica molara medie a CO₂  intre 0 si 100 ^oC.

17. Sa se calculeze variatia de entropie pentu 1 mol care trece din starea 1, gaz la temperatura de fierbere si 1 atm, in starea 2, solid la temperatura de cristalizare si presiunea de 1 atm.

18. Capacitatea calorica molara la presiune constanta a MnO₂ in intervalul 298-780 ^oC este data de ecuatia:

Sa se arate ca:

19. Sa se calculeze ΔG la 100 ^oC pentru 1 mol apa, daca presiunea creste cu 1 atm. (Se va considera apa lichida incompresibila).

20. Temperatura unui gaz ideal creste de la 25 la 250 ^oC. Sa se calculeze variatia de presiune a gazului, necesara unei variatii nule de entropie intr-un asemenea proces.

21. O masina termica functioneaza cu doua surse de caldura identice, dar cu temperaturi diferite T₁ si T₂. Schimbul de caldura este izobar si fara a provoca transformari de faza. Sa se arate ca lucrul maxim obtinut este dat de expresia:

22. Intre doua surse de caldura identice avand temperatura initiala T₁ functioneaza o masina frigorifica care scade temperatura uneia dintre surse la T₂ (izobar, fara transformari de faza. Sa se arate ca lucrul minim necesar functionarii masinii este:

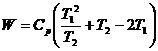
23. Intr-un vas Dewar, care contine 5 kg apa la 30 ^oC, se introduce 1 kg gheata la -10 ^oC. Sa se calculeze variatia de entropie a procesului de amestec.

24. Intr-un vas Dewar se amesteca 100 g apa la 10 ^oC cu 200 g apa la 40 ^oC. Sa se calculeze variatia de entropie si de entalpie libera a procesului de egalizare a temperaturii, considerand entropia unui mol de apa la 25 ^oC, si caldura specifica a apei .

25. Un litru gaz perfect la 0 ^oC si 1 atm este destins izoterm.

a) Sa se calculeze volumul final necesar pentru o crestere a entropiei cu ;

b) Temperatura gazului considerat este adusa la 100 ^oC, la volumul constant, si apoi gazul este destins izoterm. Sa se calculeze volumul final pentru o crestere a entropiei de ;

c) Temperatura gazului initial este adusa la 100 ^oC, la presiune constanta. Sa se calculeze volumul.

Gazul se destinde izoterm la 100 ^oC pana la volum corespunzator la o crestere a entropiei de . Sa se calculeze acest volum.

d) Sa se interpreteze rezultatele a, b, c in termeni de probabilitate.

26. Sa se calculeze ΔU, ΔH, ΔS, W, Q, ΔG si ΔF la destinderea izoterma a unui mol de gaz perfect la 25 ^oC de la 10 la 100 l.

*27. Sa se calculeze ΔU, ΔH, ΔS, W, ΔG si ΔF, presiunea si temperatura finale la comprimarea adiabatica pana la 1 l a 10 l H₂, la 0 ^oC si 1 atm, considerand si .

28. Sa se calculeze ΔU, ΔH, ΔS, W, Q, ΔG si ΔF la procesul de topire a unui mol de gheata la 0 ^oC (1 atm).

29. Reactia zincului cu ionii de cupru se conduce izoterm in trei moduri:

a) se introduce zinc intr-o solutie de azotat de cupru;

b) se construieste o pila, de exemplu:

care se descarca pe o rezistenta foarte mica;

c) pila din (b) se descarca pe o rezistenta alimentata cu o tensiune foarte apropiata de f.e.m. a pilei si de semn contrar.

In cele trei experiente se masoara caldura schimbata de pila. Sa se stabileasca procesul in care variatia de entropie este data de raportul caldura schimbata: temperatura.

30. Sa se calculeze ΔG, ΔH si ΔS pentru procesul de cristalizare a apei subracite la -5 ^oC.

31. Se amesteca adiabatic doua cantitati egale de apa (m grame), dar de temperaturi diferite T₁ si T₂. Sa se calculeze variatia de entropie a sistemului izolat.

32. La formarea AgCl din elemente, in conditii standard, variatia de entalpie libera este si caldura de reactie este la 18 ^oC. Sa se calculeze variatia de entropie corespunzatoare. Sa se calculeze variatia de entalpie libera pentru o crestere de 10 ^oC a temperaturii, presupunand ca este o constanta.

33. Variatia de entalpie libera ΔG a unui proces este la 25 ^oC si la 35 ^oC. Sa se calculeze ΔH si ΔS pentru procesul efectuat la 30 ^oC.

34. Presiunea de vapori a mercurului la 160 ^oC este 4,19 mm col. Hg. Sa se calculeze variatia de entalpie libera (in ergi) pentru procesul de comprimare izoterma a unui mol de mercur de la starea de vapori in echilibru cu lichidul la 160 ^oC, in starea de vapori la 1 atm si 160 ^oC.

35. Sa se calculeze variatia de entalpie libera pentru procesul de trecere a unui mol de benzen la 25 ^oC din lichidul pur intr-o solutie ideala care contine 1 mol benzen la 4 moli substanta straina.

36. Un sistem este constituit din n lichide diferite, necompresibile, cu capacitati calorice c_i si temperaturi (i = 1, 2 n).

Sa se calculeze temperatura finala si lucrul dat de sistem, prin egalarea temperaturilor, fara schimb de caldura cu exteriorul.

37. Sa se arate, prin evaluarea variatiei entalpiei libere, ca din cele trei procese de mai jos, primul corespunde sensului natural.

(100 ^oC)

(100 ^oC)

(100 ^oC)

*38. Sa se calculeze pentru procesul NaCl(s) → NaCl (aq; m = 6,12), stiind ca concentratia m = 6,12 corespunde saturatiei la 25 ^oC.

*39. Sa se arate ca variatia de entropie la dizolvarea NaCl(s) → NaCl (aq; m = 6,12) este aproximativ egala cu unitatea (u.e.) la 25 ^oC. Sa se calculeze ΔS pentru acelasi proces la 40 ^oC (v. problema precedenta).

40. Sa se arate ca entropia partial molara intr-o solutie tinde catre + cu cresterea dilutiei.

41. Considerand pila care functioneaza pe baza reactiei:

Ag(s) + HgCl(s) = AgCl(s) + Hg(l)

si care are f.e.m. E = 0,0455 V la 25 ^oC, sa se calculeze ΔG, ΔS si .

42. O anumita pila galvanica, in care reactia chimica decurge fara variatie de volum () are f.e.m. E = 1 V.

Daca pila este utilizata la punerea in functiune a unui motor, diferenta de potential dintre electrozii pilei este 0,9 V. Daca randamentul motorului este 90%, sa se calculeze lucrul schimbat de sistemul constituit din motor si pila, pentru fiecare coulomb care trece prin circuit, si sa se calculeze variatia de entalpie libera in pila pentru un coulomb.

43. Daca pila (considerata mai sus) este incarcata cu un generator, potentialul dintre electrozi este 1,1 V. Sa se calculeze lucrul dat pilei si variatia de entalpie libera in pila pentru un coulomb.

*44. O pila galvanica functioneaza la temperatura si presiune constante. Reactia chimica din pila are loc cu o variatie de voulm ΔV la trecerea a z. Sa se arate ca .

*45. Sa se stabileasca expresia potentialului chimic a componentului 2 intr-o solutie binara daca .

*46. Sa se verifice ecuatia:

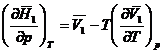
*47. Sa se arate ca:

, si

*48. De asemenea, sa se arate ca:

, si

*49. Sa se verifice ca:

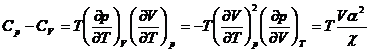
*50. Sa se verifice urmatoarele ecuatii pentru gazul perfect:

; ; ;

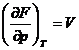*51. Sa se demonstreze ecuatiile generale:

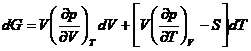
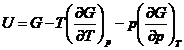
*52. Sa se verifice ecuatia (XIV.62) din text.

*53. Sa se arate ca:

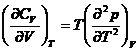
*54. Sa se arate ca:

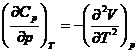
*55. Sa se demonstreze ecuatiile:

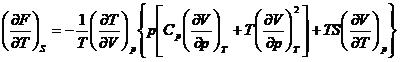
si

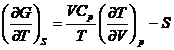
*56. Pentru o anumita substanta la 25 ^oC si 1 atm se dau urmatoarele date:

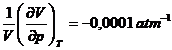, si

Sa se calculeze 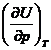 la aceasta temperatura si presiune.

*57. Pentru apa la 25 ^oC (intre 0 si 1000 atm):

S[ se calculeze lucrul de comprimare izoterma la 25 ^oC pentru 1 mol apa de la 1 la 1000 atm si ΔU, ΔH, ΔF, ΔG si ΔS in acest proces (v. exemplul 16).

58. Sa se arate ca semnul variatiei coeficientului de dilatatie cu presiunea, la temperatura constanta, este contrar semnului variatiei coeficientului de compresibilitate izoterma cu temperatura, la presiune constanta. Se poate generaliza aceasta constatare?

*59. Pentru un mol benzen la T = 298 se indica:

; si

Sa se calculeze ridicarea de temperatura a benzenului daca presiunea creste brusc cu 1 atm. Valoarea experimentala este 0,024 ^oC.

Indicatie. Se va folosi relatia:

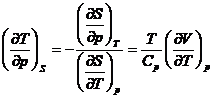
*60. Pentru benzen intre 5 si 80 ^oC (v. exemplul 16 si problema 59):

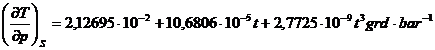
si

(t in ^oC)

Pe baza ecuatiei cunoscute (v.exemplul 16), 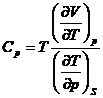, sa se calculeze C_p pentru benzen, in Joule si , la 20, 50, 80 ^oC si sa se compare cu valorile din tabele.

*61. La presiune obisnuita coeficientul de dilatatie α si caldura specifica c_p a apei au urmatoarele valori:

Volumul specific al apei in acelasi domeniu de presiune este dat de ecuatia:

a) Sa se stabileasca ecuatia incalzirii adiabatice a apei pentru o crestere a presiunii cu 1 atm, la diferite temperaturi, si sa se compare cu ecuatia experimentala .

b) La presiunea de 500 atm, incalzirea adiabatica este data de ecuatia:

Valorile coeficientilor de dilatatie si volumele specifice ale apei la diferite temperaturi pentru acest domeniu de presiune sunt:

Sa se calculeze valorile caldurii specifice in acest domeniu de presiune (500 atm).

62. La 200 K coeficientul de dilatatie al mercurului solid este

Coeficientul de compresibilitate izoterma este , volumul molecular este , .

Sa se calculeze C_p-C_V, C_V pentru mercurul solid la 200 K.

63. Iodul solid are la 20 ^oC un coeficient de dilatatie liniara de si un coeficient de compresibilitate izoterma de .

Sa se calculeze C_p-C_V si C_V pentru , daca si densitatea este .

64. Intre 0 si 10 ^oC, volumul specific si caldura specifica (la presiune constanta) a apei la presiunea atmosferica sunt date de ecuatiile:

Coeficientul de compresibilitate izoterma:

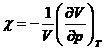este

a) Sa se calculeze C_p si C_V pentru t₁ = 0 ^oC si t₂ = 10 ^oC.

b) Sa se calculeze valorile derivatelor partiale si la 0 ^oC si presiunea atmosferica.

c) In general, volumul specific al apei trebuie exprimat sub forma: , unde a, b, c sunt functii de presiune.

Sa se calculeze marimea 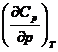  la p = 1atm si 0 ^oC.

*65. Valoarea aproximativa a presiunii interne a azotului este la 1 atm si 0 ^oC. Sa se calculeze α si sa se arate, in procente, abaterea de la relatia , considerand valabila legea Boyle-Mariotte.

66. Doua rezervoare contin gaze diferite in aceleasi conditii.

a) Sa se arate ca variatia de entropie la interdifuziunea a j moli de gaz (1) si 2 j moli gaz (2) este:

b) Sa se calculeze variatia de entropie pentru j = 0; 0,5; 1; 1,5; 2. Sa se reprezinte grafic.

*67. Un fir de otel de 10 m lungime are o densitate de , caldura specifica , coeficientul de dilatatie liniara , modulul Young CGS si un diametru de 2 mm. Temperatura mediului este de 300 K.

a) Sa se calculeze alungirea firului la temperatura constanta pentru o tractiune de 50 kg;

b) Considerand ca tractiunea decurge reversibil si firul este izolat termic, sa se calculeze variatia temperaturii firului.

*68. Firul de otel considerat in problema precedenta este rasucit. Constanta de torsiune este , si .

a) Sa se calculeze cuplul aplicat firului la temperatura constanta pentru o rasucire de 10 rad.

b) Presupunand rasucirea reversibila si adiabatica sa se calculeze variatia de temperatura a firului.

69. Sa se reprezinte grafic procesul de incalzire la volum constant, in diferite perechi de coordonate p, V, T, U, H, S.

70. Entalpia de formare a solutiei solide NaCl(1) - NaBr(2) se determina din diferenta dintre caldura de dizolvare in apa a solutiei solide si caldura de dizolvare a componentelor pure.

Experienta stabileste expresia entalpiei de formare a unui mol solutie solida: (x = fractia molara), valabila intre 0 si 350 K. Considerand ca expresia entropiei de amestec corespunde solutiei ideale, sa se calculeze variatia de entalpie libera la formarea unui mol solutie solida cu o compozitie la 100 K.