Functii termodinamice. Criteriile de proces natural.

Functii termodinamice. Criteriile de proces natural

Functiile termodinamice (de diferite variabile de stare ale sistemului) permit o exprimare imediata a proprietatilor sistemului prin valorile lor sau a variatiilor lor, sau prin derivatele partiale de diferite ordine in raport cu variabilele corespunzatoare. In afara de entropie, ca functii termodinamice se folosesc energia interna (U), entalpia (H), energia libera definita prin F = U - TZ (Helmholtz) si entalpia libera G = H - TS (Gibbs).

U, H, F si G poarta si denumirea de potentiale termodinamice, deoarece variatiile lor in anumite conditii reprezinta lucrul schimbat de sistem.

Toate aceste functii sunt marimi extensive. Valoarea functiei pentru un sistem eterogen este data de suma valorilor pentru fiecare faza. Variabilele corespunzatoare fiecarei functii se pot fixa cu ajutorul schemei de mai jos. De exemplu: U = U(S,V), H = H(S,p), G = G(p,T), etc. La fiecare functie corespund deci variabilele asezate in schema de o parte si de alta a functiei.  

a) Potrivit principiului intai si al doilea se poate scrie:

   (XIV.10)

Pentru S constant si δW = 0, rezulta:

(XIV.10a)

deci criteriul de proces natural in aceste conditii este constituit de descresterea energiei interne. Pentru ecuatia (XIV.10a) se aplica la S si V constant.

b) Conform ecuatiei principiului intai, , se obtine:

dH = TdS + Vdp - δQ'(XIV.11)

(numai pentru ).

Analog relatiilor de mai sus, pentru dS = 0 si dp = 0 rezulta:

(XIV.11a)

ceea ce indica descresterea entalpiei drept criteriu de proces natural.

c) Introducand energia libera F = U - TS, se obtine:

dF = -SdT + δW - δQ'(XIV.12)

Pentru T = const, dF = δW - δQ' si daca procesul este reversibil (δQ' = 0) rezulta:

(XIV.12a)

(notand lucrul dat de sistem W_d = -W).

Pentru un proces izoterm natural (δQ' > 0):

(XIV.12b)

Aceste relatii arata ca lucrul maxim dat de sistem corespunde variatiei cu semn schimbat a energiei libere.

Pentru dT = 0 si se obtine:

(XIV.12c)

ceea ce arata ca procesul natural corespunde, in aceste conditii, la o descrestere a energiei libere.

d) Utilizand entalpia libera G = H - TS = U + pV - TS, se obtine pentru un proces infinitezimal:

dG = - SdT + δW + d(pV) - δQ' (XIV.13)

Pentru dT = 0 si dp = 0:

δQ' = - dG + δW + pdV 0 

daca procesul este reversibil (δQ' = 0):

sau

    (XIV.13a)

de unde rezulta ca, pentru un proces izoterm-izobar reversibil, descresterea entalpiei libere este egala cu lucrul util (maxim) dat de sistem (din lucrul total s-a scazut lucrul de presiune).

Pentru un proces izoterm-izobar natural:

(XIV.13b)

Daca ecuatia (XIV.13) devine: dG = -SdT + Vdp - δQ' si pentru un proces izoterm-izobar dG = -δQ' 0. Criteriul de proces natural, in aceste conditii, este constituit de descresterea entalpiei libere.

Conditia de proces izoterm in ecuatiile (XVI.12a) si (XVI.13a) nu reprezinta o restrangere a generalitatii definitiilor energiei libere si entalpiei libere. Lucrul schimbat de sistem este maxim numai atunci cand sistemul are, inainte si dupa transformare, aceeasi temperatura cu mediul inconjurator.Toate transformarile importante in chimie si tehnica trebuie considerate ca monoterme (au loc cu schimb de caldura cu mediul inconjurator, dar temperatura acestuia ramane practic constanta).

Variatiile de energie libera si entalpie libera nu se pot calcula decat pentru procese reversibile care trebuie asociate intotdeauna procesului natural (ireversibil).

Trebuie sa se remarce faptul ca observatiile facute in ultimele randuri permit stabilirea teoremei lui Carnot si pe baza entalpiei libere. Aceasta remarca este deosebit de importanta in cazul proceselor continue. Teorema lui Carnot (care poate constitui un mod de enuntare a principiului al doilea) afirma ca, dintre toate ciclurile posibile care opereaza intre limite date de temperatura, randamentul termic (mai corect, factorul de conversie, v. exemplul XI.11) al ciclului Carnot (doua izoterme, doua adiabate) reversibil este cel mai mare:

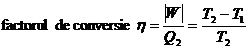
(pentru ciclul Carnot reversibil).

Exemplul 9. O masina frigorifica functioneaza intr-un mediu cu o temperatura de 25 ^oC. Sa se calculeze lucrul minim necesar solidificarii a 1000 g apa la 0 ^oC si cantitatea de caldura schimbata de masina cu mediul inconjurator.

Rezolvare:

Potrivit teoremei lui Carnot, lucrul minim (reversibil) dat de o masina este:

(caldura specifica de topire a ghetii este 80 cal · g^-1).

Lucrul dat masinii (schimbat) este deci 7300 cal. Acelasi rezultat se obtine folosind relatia:

Cantitatea de caldura schimbata cu mediul inconjurator rezulta din expresia principiului intai, , de unde:

care reprezinta (in valoare absoluta) caldura cedata de masina mediului inconjurator.

Exemplul 10. Sa se calculeze lucrul minim necesar racirii unui mol CO₂ gaz la 1atm, de la +10 la -10 ^oC, daca mediul inconjurator in care functioneaza masina are o temperatura de +10 ^oC.

Rezolvare:

Potrivit teoremei lui Carnot:

si, deoarece la fiecare temperatura se schimba numai o cantitate infinitezimala de caldura, rezulta:

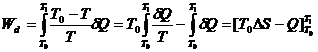
Pentru o transformare izobara Q =H si astfel, conform celor aratate, se obtine:

Considerand in intervalul de temperatura (-10 ^oC pana la +10 ^oC) capacitatea calorica , se obtine:

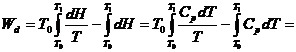
Exemplul 11. O instalatie propusa pentru utilizarea radiatiilor solare contine un lichid organic, care se incalzeste de la -3 la 37 ^oC, la presiune constanta. Sa se calculeze fractiunea maxima de energie utilizabila la o temperatura a mediului egala cu -23 ^oC.

Rezolvare:

Energia absorbita pe 1 mol de lichid este , iar entalpia libera este .

Fractiunea utilizabila de energie absorbita (valoarea maxima) este:

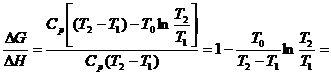
Exemplul 12. Sa se calculeze marimile W, Q, ΔU, ΔH, ΔS, ΔF si ΔG pentru comprimarea izoterma a unui mol de gaz perfect de la 1 atm la 10 atm, la 1000 K.

Rezolvare:

Conform ecuatiilor cunoscute (v. cap. XI), deoarece si , se obtine:

Din ecuatia (XIV.6) rezulta, in cazul reversibilitatii:

u.e. (unitati entropice)

Prin integrarea ecuatiilor (XVI.12) si (XIV.13) se obtine:

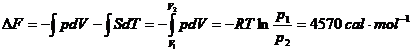
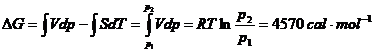
Exemplul 13. Sa se calculeze:

a) capacitatile calorice la presiune constanta si volum constant ;

b) entalpia H;

c) energia interna U;

d) entropia S;

e) entalpia libera G pentru 1 mol de azot la 500 ^oC si 100 atm presupunand gazul perfect.

Rezolvare:

a) La 500 ^oC si 1 atm . In aceleasi conditii:

si sunt independente de presiune.

b) In acest caz:

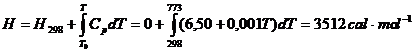
considerand arbitrar valoarea .

Deoarece pentru gazul perfect 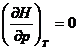, entalpia azotului la 773 K si 100 atm este 3512 , egala cu entalpia azotului la 1 atm si 773 K.

c) In mod asemanator cu calculul entalpiei, se obtine:

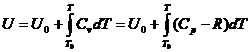
dar mai usor se poate calcula prin ecuatia:

(la 500 ^oC si 1 atm si la 500 ^oC si 100 atm, deoarece).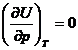

d)

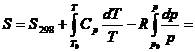
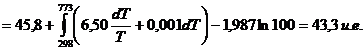
observand in tabele (v. cap. XV), ca entropia in conditii standard este

e) Prin integrare, din dG = Vdp - SdT, se obtine:

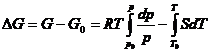
Deoarece 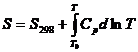(la presiune constanta), rezulta:

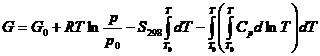
In loc de a utiliza aceasta relatie, se poate calcula mai simplu:

Aceasta valoare nu are o semnificatie absoluta, deoarece este bazata pe valoarea arbitrara .

Este important de remarcat faptul ca ΔH, ΔU si ΔS sunt independente de valoarea aleasa a starii initiale. Aceasta nu mai adevarat pentru ΔF si ΔG. Se vede ca ΔG depinde de valoarea aleasa a lui S₂₉₈ si, deoarece pentru fiecare proces ΔG trebuie sa aiba o valoare definita, ΔG nu poate fi calculat din date termice, decat daca se considera valorile absolute ale entropiei (v. cap. XV).