
|
|
|
Cererea si preturile
Relatia dintre cantitatea ceruta de un consumator dintr‑un anumit bun si nivelul pretului sau este exprimata de functia cererii in raport de pret.
1. Functia de cerere
1.1. Constructia curbei cererii individuale
Curba cererii individuale pentru un anumit bun arata cum evolueaza cererea unui individ pentru acel bun atunci cand pretul acestuia variaza. Pentru a o construi, putem folosi exemplul luat pentru analiza echilibrului consumatorului, reprezentat grafic in fig. 3.10. Daca vom inlocui in aceasta figura, pe ordonata, cantitatile din bunul Y cu diferitele niveluri de pret, Px, ale bunului X, iar pe abscisa vom lasa cantitatile din bunul X, vom obtine in fig. o curba care descrie modul cum se modifica cererea unui individ pentru bunul X atunci cand variaza pretul acestui bun, adica reprezentarea grafica a functiei X = f(Px). Astfel, pentru Px = 10 u.m., cererea individului pentru bunul X corespunzatoare punctului de echilibru E1, este de 2 unitati, ceea ce reprezinta coordonatele punctului A(2,10). Cand Px scade la 4 u.m., cererea individului pentru bunul X, corespunzatoare punctului de echilibru E2, se mareste la 5 unitati. Astfel avem coordonatele punctului B(4,5). Iar cand Px scade la 2, cererea individului pentru bunul X, corespunzatoare punctului de echilibru E3, se ridica la 10, ceea ce se inseamna ca punctul C are coordonatele 10 si 2. Punctele A, B si C ne orienteaza doar in trasarea curbei cererii. Cu numai trei puncte, aceasta curba nu poate fi decat aproximativa. Ne‑ar fi trebuit un numar foarte mare de puncte de echilibru pentru a obtine o imagine relativ fiabila a evolutiei cererii la variatia pretului.
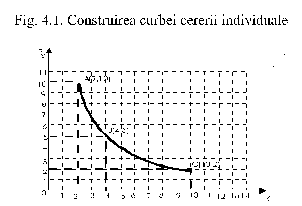
Curba cererii descrie prima lege a cererii: cererea unui bun este functie descrescatoare de pretul sau. Desigur ca acest rezultat nu este valabil decat in conditiile 'caeteris paribus', adica daca toate celelalte elemente - si in special pretul altor bunuri, venitul consumatorului, climatul economic si social‑politic ‑ nu variaza.
1.2. Ecuatia unei functiide cerere liniare si interpretarea ei
Pentru simplificarea calculelor, sa presupunem ca o reprezentare corecta a ansamblului curbei cererii ar fi obtinuta doar prin unirea punctelor A(2,10) si C(10,2). Aceasta ar insemna ca dependenta cantitatii cerute fata de pret este liniara, curba cererii prezentandu‑se sub forma unei drepte, ca in fig. 4.2.
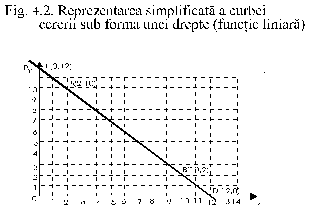
Dupa cum s‑a aratat si mai sus, la constrangerea bugetara, ecuatia unei drepte este de forma y = ax + b, unde 'a' masoara panta dreptei, iar 'b' este o constanta (nivelul minim sau maxim - depinde de semnul lui 'a' - al lui Y, independent de nivelul lui X). Prin analogie cu aceasta expresie generala a ecuatiei unei drepte, se poate scrie ecuatia cererii pentru un bun X sub forma:
![]() ()
()
unde X este cantitatea ceruta din bunul X si care variaza in functie de pretul Px al acestui bun, iar a<0, deoarece intre X si Px, conform primei legi a cererii, exista o relatie inversa sau descrescanda. Am putea scrie ecuatia dreptei AC daca am avea valoarea necunoscutelor a si b. Pentru a le determina, rezolvam sistemul de doua ecuatii cu doua necunoscute de mai jos:
![]() (4.2.)
(4.2.)
deoarece punctul A(X=2; Px=10) este situat pe dreapta cererii, iar coordonatele lui trebuie sa verifice ecuatia
![]() (4.3.)
(4.3.)
deoarece si punctul C de coordonate X=10 iar Px=2 este situat pe dreapta cererii, iar coordonatele lui trebuie sa verifice ecuatia
Rezolvand sistemul format din ecuatiile 4.2. si 4.3., obtinem: a=-1, iar b=12.
Rezulta ca ecuatia functiei de cerere exprimata grafic prin dreapta din fig. 4.2. este:
![]() (4.4.)
(4.4.)
Cum interpretam aceasta ecuatie? Faptul ca nu exista decat o singura variabila explicativa, Px, nu inseamna ca volumul cererii de consum pentru bunul X este influentat numai de pretul acestui bun, asa cum s‑ar putea crede la prima vedere. Ecuatia 4.4. indica faptul ca daca se mentin neschimbate toate celelalte variabile susceptibile a afecta consumul bunului X, acesta evolueaza conform relatiei X = - Px+12.
De exemplu, ecuatia completa a cererii ar putea fi:
![]() (4.5.)
(4.5.)
unde P reprezinta nivelul general al preturilor celorlalte bunuri, iar V venitul. Cunoscand valorile acestor variabile in momentul studierii cererii in functie de pretul lui X, de exemplu, Py = 5, P = 10, iar V = 60 si inlocuindu‑le in ecuatia 4.5., obtinem:
![]()
adica X = -Px + 12; deci numarul 12 cuprinde singur efectul tuturor celorlalti factori de influenta pe care i‑am presupus constanti.
In aceasta forma, ecuatia functiei de cerere indica faptul ca cererea maxima pentru bunul X, de 12 unitati, este atunci cand pretul acestuia devine 0. Se observa, din fig. 4.2., ca, dincolo de punctul D(12,0), nevoia este saturata, iar utilitatea marginala devine negativa. La cealalta extremitate a 'curbei' cererii, in punctul E(0,12), pretul maxim pe care cumparatorul consumator este dispus sa‑l plateasca pentru bunul X este inferior lui 12 deoarece daca Px = 12, cererea pentru bunul X ar deveni zero.
2. Efectul de substitutie (efectul de pret pur) si efectul
de venit: definirea si delimitarea lor
Deci, cererea pentru un anumit bun este o functie descrescanda de pret, toate celelalte conditii ramanand neschimbate (clauza caeteris paribus). Am vazut insa deja, in paragraful 3.3.5.3., ca variatia lui Px nu lasa in realitate toate celelalte conditii neschimbate. Rezultatul variatiei lui Px poate fi descompus in doua efecte:
A. Efectul de substitutie (numit si efectul pret), care masoara variatia din cererea pentru un bun provocata de schimbarea pretului sau relativ, in conditiile mentinerii constante a venitului real, adica a nivelului de utilitate oferit de noile combinatii de bunuri
Acest efect va fi mereu negativ, deoarece variatia pretului relativ al unui bun in raport cu alte bunuri substituibile va antrena intotdeauna o variatie in sens invers a consumului sau. Astfel, o crestere a lui Pxin raport cu Py va incita intotdeauna pe consumatorul rational sa diminueze consumul lui X, pentru a‑l substitui cu Y, care, desi nu si‑a modificat pretul propriu, a devenit mai ieftin ca urmare a scumpirii lui X. Dimpotriva, o reducere a lui Px va antrena substituirea bunului Y de catre bunul X.
Construind curba cererii in maniera folosita la fig. , am presupus implicit ca intreaga variatie a cererii pentru bunul X era provocata numai de efectul pret, ceea ce nu este tocmai exact. Pentru a fi construit o curba a cererii determinate strict de efectul pret, pe care o putem numi curba de cerere compensata, ar fi trebuit sa eliminam partea variatiilor de consum determinate de modificarea puterii de cumparare sau a venitului real, deci efectul venit.
Curba cererii compensate exprima relatia de dependenta intre pretul unui bun si cantitatea ceruta din el, in conditiile mentinerii constante a preturilor celorlalte bunuri si a utilitatii sau venitului real.
B. Efectul venit, masoara variatia cererii pentru un anumit bun, provocata de modificarea venitului real sau utilitatii, ca urmare a variatiei pretului unui bun, in conditiile mentinerii neschimbate a preturilor celorlalte bunuri si a venitului nominal.
De aceasta data, mentinem neschimbat venitul nominal. Cand bunul X se ieftineste. adica Px se diminueaza, puterea de cumparare sau 'venitul real' al individului creste. Cu acelasi venit nominal, consumatorul va putea mari cantitatea cumparata din bunul X, nu prin substituirea lui Y ‑ cand si‑ar fi mentinut neschimbat nivelul utilitatii, ramanand pe aceeasi curba de indiferenta ‑ ci, pentru ca, bunul X devenind mai ieftin, cu acelasi venit nominal poate cumpara mai multe unitati din acest bun. In felul acesta individul isi mareste nivelul satisfactiei obtinute cu acelasi venit nominal, deplasandu‑se pe o curba de indiferenta situata la dreapta, mai ridicata. Si invers, daca Px se majoreaza, cu acelasi venit nominal individul isi va putea procura o cantitate mai mica din bunul X, adica puterea de cumparare sau venitul sau real se diminueaza, determinand plasarea consumatorului pe o curba de indiferenta situata mai la stanga, cu un nivel de utilitate mai scazut.
Deci, ca urmare a efectului venit, cererea pentru bunul X creste atunci cand pretul sau se diminueaza provocand sporirea venitului real sau a puterii de cumparare a venitului nominal ramas neschimbat; cererea pentru bunul X scade atunci cand pretul acestuia creste, provocand diminuarea venitului real sau puterii de cumparare a venitului nominal ramas neschimbat. Regasim astfel continutul primei legi a cererii, care exprima interdependenta dintre variatia cererii pentru un anumit bun si variatia pretului bunului respectiv.
C. Delimitarea efectului de substitutie si a efectului de venit
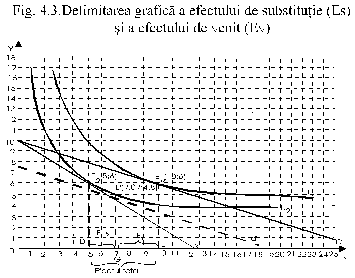
Cele doua efecte ale modificarii pretului bunului X in conditiile mentinerii neschimbate a preturilor celorlalte bunuri si a venitului nominal se produc concomitent. Cum putem delimita variatia din cererea pentru bunul X datorata efectului de substitutie si cea datorata efectului de venit? Sa revenim la exemplul din paragraful 3.3.5.2 cu reprezentarea grafica din fig. 3.10 si sa plecam de aceasta data de la punctul de echilibru al consumatorului E2, care reprezinta combinatia optimala de 5 unitati din bunul X si 6 unitati din bunul Y, in conditiile unui venit monetar de 50 u.m., a preturilor Px = 4 u.m. iar Py = 5 u.m. si a unei functii de utilitate definite de ecuatia U = U(X, Y) = X(Y-2). Daca pretul bunului X se diminueaza de la Px = 4 u.m. la Px = 2.u.m., toate celelalte (adica pretul Py, venitul nominal V si functia de utilitate) ramanand neschimbate, noul punct de echilibru al consumatorului (noua combinatie optimala) devine punctul E3, de coordonate 10 si 6 (adica acea combinatie sau 'cos de consum' formata din 10 unitati din bunul X si 6 unitati din bunul Y). Deci, fata de situatia anterioara, cererea individului pentru bunul X a crescut cu 5 unitati. Intrebarea este: cat din aceasta variatie este datorata efectului de substitutie (Es) si cat efectului de venit (Ev). Raspunsul il putem afla folosindu‑ne de reprezentarea grafica din fig. 4.3.
Pentru
determinarea efectului de substitutie, pornind de la definitia acestuia,
trebuie sa ne mentinem in continuare pe curba de indiferenta U2
(deoarece nivelul utilitatii sau 'venitului real' nu se modifica),
substituind bunul Y cu bunul X pana in punctul in care RMS devine egala cu noul
raport de preturi ![]() . Coordonatele acestui punct (E') le determinam dintr‑un
sistem format din alte doua ecuatii:
. Coordonatele acestui punct (E') le determinam dintr‑un
sistem format din alte doua ecuatii:![]() , adica
, adica ![]() , ceea ce inseamna:
, ceea ce inseamna:
![]() sau
sau ![]() (4.6)
(4.6)
si:
![]() , adica
, adica ![]() (4.7)
(4.7)
Din ecuatiile
4.6 si 4.7 rezulta: ![]()
![]() , iar
, iar ![]() .
.
Deci, punctul E' va avea coordonatele 7,07 si 4,8, ceea ce inseamna ca in conditiile noului raport de preturi, aceeasi utilitate U2 ar fi obtinuta prin consumarea a 7,07 unitati din bunul X si 4,8 unitati din bunul Y, dar cu cheltuiala de numai 7,072+4,85=38,14 u.m.. Deci, efectul pur de substitutie, definit ca variatie a cererii pentru produsul X determinata numai de variatia pretului acestui bun in conditiile mentinerii neschimbate a utilitatii (sau, 'venitului real' sau puterii de cumparare) si preturilor celorlalte bunuri (in speta, a bunului Y) este diferenta dintre cantitatea ceruta din X in punctul E' si cea ceruta din X in punctul E2:
![]()
Ca urmare insa a faptului ca venitul nominal al consumatorului ramane neschimbat, de 50 u.m., fata de 38,14 u.m. cat ii sunt necesare in punctul E', individul isi poate permite sa consume mai mult si din bunul X si din bunul Y, asa cum indica punctul de echilibru E3 de coordonate (10;6). Variatia cantitatii cerute din bunul X ca urmare a cresterii nivelului utilitatii sau 'venitului real' datorate reducerii pretului bunului X, in conditiile mentinerii neschimbate a venitului monetar si pretului bunului Y este egala cu 10-7,07 = 2,93 si reprezinta tocmai efectul de venit.
Deci, efectul total al modificarii pretului Px asupra cererii acestui bun, de 5 unitati, se descompune in:
efect pur de substitutie, de 2,07 unitati
efect de venit, de 2,93 unitati.
Pentru determinarea grafica a efectului de substitutie si a celui de venit, se procedeaza astfel (vezi fig. 4.3.):
1. Se pleaca de la datele initiale: Px=4 u.m.; Py=5.u.m.; V=50 u.m.; U=U(X,Y)=X(Y-2), pe baza carora se traseaza dreapta bugetara AB si se determina punctul de echilibru E2(5;6), situat pe curba de indiferenta U2, a carei ecuatie este:
![]()
2. Daca Px se reduce la Px=2 u.m., toate celelalte date ramanand neschimbate, trasam noua dreapta bugetara AC si determinam noul punct de echilibru E3(10;6) prin care vom duce noua curba de indiferenta U3, avand ca ecuatie:
![]()
3. Proiectiile punctelor de echilibru E2 si E3 pe abscisa sunt D(5;0) si, respectiv, F(10;0). Segmentul DF, avand o marime egala cu 5 unitati din bunul X, reprezinta efectul total al reducerii lui Px.
4. Pentru
determinarea efectului de substitutie, conform definitiei sale, trebuie sa ne
mentinem pe curba de indiferenta U2, dar sa ajungem in acel punct al
ei in care RMS sau panta este egala cu noul raport de preturi ![]() , conditia de optimalitate a alegerii consumatorului. Daca
s-au trasat corect curbele U2 si U3, ca si dreapta AC,
punctul pe care‑l cautam, E', il descoperim ducand la curba U2
o tangenta paralela cu dreapta AC. Punctul de tangenta al dreptei d', paralela
cu
, conditia de optimalitate a alegerii consumatorului. Daca
s-au trasat corect curbele U2 si U3, ca si dreapta AC,
punctul pe care‑l cautam, E', il descoperim ducand la curba U2
o tangenta paralela cu dreapta AC. Punctul de tangenta al dreptei d', paralela
cu ![]() , la curba U2 este exact punctul E', a carui
proiectie pe abscisa este punctul G, de
coordonate (7,07 si 0) .
Segmentul
, la curba U2 este exact punctul E', a carui
proiectie pe abscisa este punctul G, de
coordonate (7,07 si 0) .
Segmentul ![]() reprezinta efectul pur de substitutie, deoarece intre punctele E2 si E'
nivelul utilitatii sau venitului real ramane neschimbat, pentru ca suntem pe
aceeasi curba de indiferenta, U2, modificandu‑se doar panta
sau RMS ca urmare a modificarii raportului dintre preturile celor doua bunuri;
reprezinta efectul pur de substitutie, deoarece intre punctele E2 si E'
nivelul utilitatii sau venitului real ramane neschimbat, pentru ca suntem pe
aceeasi curba de indiferenta, U2, modificandu‑se doar panta
sau RMS ca urmare a modificarii raportului dintre preturile celor doua bunuri; ![]() , diferenta pana la efectul total, nu este altceva decat
efectul de venit, care masoara rezultatul ridicarii puterii de cumparare
provocate de scaderea lui Px. Intre punctele E' si E3 numai nivelul venitului real se schimba
(consumatorul plasandu‑se pe o curba de indiferenta mai ridicata), dar
raportul preturilor este mentinut constant, panta fiind aceeasi in E' si E3.
, diferenta pana la efectul total, nu este altceva decat
efectul de venit, care masoara rezultatul ridicarii puterii de cumparare
provocate de scaderea lui Px. Intre punctele E' si E3 numai nivelul venitului real se schimba
(consumatorul plasandu‑se pe o curba de indiferenta mai ridicata), dar
raportul preturilor este mentinut constant, panta fiind aceeasi in E' si E3.
3. Paradoxul lui Giffen
Din exemplul de mai sus se observa ca efectul de substitutie si efectul de venit se completeaza unul pe altul, fiind de acelasi semn. Astfel, cresterea cantitatii cerute din bunul X ca urmare a reducerii pretului acestuia este datorata, pe de o parte, substituirii bunului Y de catre bunul X devenit relativ mai ieftin, iar pe de alta parte, cresterii puterii de cumparare a venitului nominal ramas nemodificat, exprimata in unitati din bunul X ieftinit. La fel se intampla si in cazul cresterii pretului unui bun: aceasta provoaca, pe de o parte, substituirea bunului scumpit de catre alt bun devenit relativ mai ieftin, iar, pe de alta parte, cresterea pretului, reducand puterea de cumparare a individului (cand toate celelalte conditii raman neschimbate), determina o reducere si intr‑o mai mare masura a cererii pentru bunul devenit relativ mai scump. Chiar daca ponderea fiecaruia dintre aceste efecte nu poate fi prea usor determinata, rezultatul global al cresterii pretului unuia dintre cele doua bunuri din 'cosul' de consum este mai mult decat evident: consumul sau cererea pentru bunul respectiv se va diminua. In cazul scaderii acestui pret, consumul sau cererea pentru bunul respectiv va creste. Acesta este cazul general.
In cazul unor populatii cu venit scazut exista insa anumite bunuri si in special cele de stricta necesitate, dar considerate de catre consumator 'inferioare', cum ar fi cartofii, carnea cu os si grasime, painea neagra etc., la care cresterea pretului nu mai determina reducerea cererii sau consumului lor, ci, dimpotriva, sporirea acestuia. De ce? Puterea de cumparare a consumatorilor saraci fiind limitata, cresterea pretului la produsele de stricta necesitate ii obliga sa renunte la consumul altor bunuri, de mai buna calitate dar mai scumpe, si sa le inlocuiasca cu cele 'inferioare', dar oricum relativ mai ieftine, chiar daca pretul lor a crescut. In acest caz, efectul venit este negativ: consumul sau cererea de bunuri carora li se majoreaza pretul sporeste in loc sa se diminueze. Cand nivelul de trai se imbunatateste prin cresterea veniturilor, consumatorul isi va diminua cererea pentru aceste bunuri 'inferioare' in favoarea bunurilor 'normale'. Dimpotriva, cererea pentru ele creste la o majorare a pretului lor atunci cand nivelul de trai se inrautateste, cand veniturile se reduc.
Acest comportament aparent paradoxal este denumit Paradoxul lui Giffen, dupa numele economistului englez care a constatat o astfel de situatie in Irlanda secolului al XIX‑lea, unde, ca urmare a cresterii generale a preturilor produselor agricole din cauza unei recolte proaste, taranii, saraciti, si‑au orientat resursele lor limitate spre procurarea cartofilor pentru a‑si asigura hrana, marind astfel cererea pentru ei, desi si pretul acestora se ridicase.
Prezentarea 'paradoxului lui Giffen' are importanta pentru a ne face sa intelegem de ce este necesara distinctia intre efectul ‑ pret si efectul venit. Prima lege a cererii, adica cererea este o functie descrescatoare de pret, este valabila daca luam in considerare doar efectul de substituire, deci efectul pur al schimbarii preturilor relative. Efectul venit provocat de modificarea pretului poate determina o evolutie inversa a cererii fata de cea prezisa de prima lege a ei.
4. De la cererea individuala la cererea pietei
Pana aici ne‑am ocupat de cererea consumatorului individual. Concluziile desprinse le putem extinde insa la intreaga cerere a pietei pentru un anumit produs, daca vom presupune ca toti purtatorii acestei cereri sunt confruntati cu acelasi pret, fara ca cererea unora sa fie influentata de cererea altora. In aceste conditii, cererea totala exprimata pentru fiecare nivel de pret este suma cererilor individuale corespunzatoare. Grafic, reprezentarea cererii totale a pietei unui anumit bun se determina prin asa‑numita 'insumare pe orizontala'. Daca presupunem ca cererea totala de pe o piata este formata din doua cereri individuale, conform tabelului de mai jos, atunci se observa ca, pentru fiecare nivel de pret, cererea pietei va fi suma cererilor individuale corespunzatoare.
Tebelul nr. ‑ Formarea cererii totale a pietei
Pretul
(u.m./buc.)
Cererea
individuala C1
Cererea
individuala
C2
Cererea
totala a
pietei
200
150
110
80
60
50
20
30
60
100
150
220
10
20
40
70
120
180
30
50
100
170
270
400
Pentru a prezenta grafic, dupa ce trasam curbele cererilor individuale, vom determina punctele curbei cererii totale a pietei insumand 'pe orizontala' cantitatile individuale corespunzatoare fiecarui nivel de pret si apoi le vom uni.
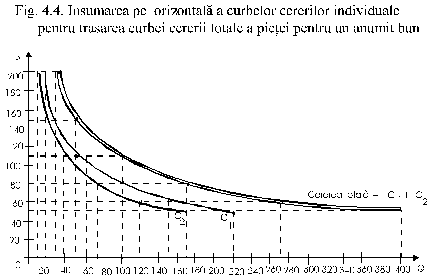
Aceeasi maniera va fi folosita si pentru 'n' cereri individuale de pe piata unui bun oarecare.
In continuare, toate rationamentele vor fi efectuate in termeni de cerere totala pentru un bun.
5. Elasticitatea cererii fata de pret
In general, conceptul de elasticitate a unei marimi exprima gradul de sensibilitate a marimii respective la variatiile survenite in factorii care o influenteaza.
Cererea pietei pentru un bun oarecare sufera influenta a numerosi factori, dar mai usor cuantificabila este cea manifestata de propriul pret, de preturile altor bunuri si de venitul consumatorilor purtatori ai cererii. Alti factori ar putea fi variatia numarului populatiei unei anumite regiuni, informatiile privind modificarea calitatii bunurilor respective, aparitia unor substituenti, anticiparile legate de evolutia inflatiei etc.
Avand in vedere posibilitatile de determinare, vom studia in continuare elasticitatea cererii pentru un bun in functie de propriul sau pret, denumita pe scurt si elasticitatea ‑ pret, elasticitatea cererii pentru un bun in functie de pretul altui bun, denumita pe scurt elasticitate pret incrucisata si elasticitatea cererii in functie de venitul consumatorilor, denumita pe scurt elasticitate‑venit.
5.1. Elasticitatea cererii unui bun fata de propriul lui pret
Sa mai precizam ca inclinatia curbei cererii unui anumit bun in functie de pretul sau depinde si de modul de alegere a scarii pe cele doua axe de coordonate. Astfel, de exemplu, cele doua curbe din fig. 4.5. de mai jos reprezinta una si aceeasi curba a cererii, trasata conform corelatiilor exprimate in tab. intre pret si cererea totala a pietei, numai ca in partea a) segmentele de pe ordonata sunt egale cu cele de pe abscisa, in timp ce in partea b) segmentele de pe abscisa sunt de trei ori mai mici fiecare decat cele de pe ordonata.
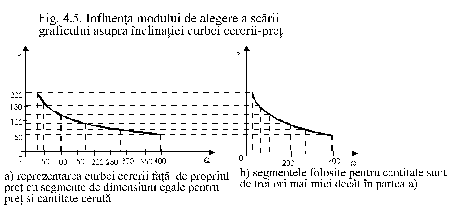
Deci, firesc, deoarece distantele de pe abscisa graficului din dreapta sunt de trei ori mai mici decat cele de pe graficul din stanga, panta curbei b) este de trei ori mai mare decat panta curbei a).
Si‑atunci, pentru a putea masura reactia cererii pentru un bun la variatiile propriului pret, in vederea compararii cu situatia altor bunuri, indiferent de scara folosita pentru reprezentarea grafica, este necesar sa operam cu exprimari procentuale. Asa ajungem la conceptul de elasticitate a cererii in diferitele sale variante.
Elasticitatea ‑ pret a
cererii pentru un anumit bun reprezinta gradul de sensibilitate a cererii sau
reactia ei la variatiile intervenite in nivelul pretului bunului respectiv. Ea se
determina ca raport intre procentul de variatie a cantitatii cerute si
procentul de variatie a pretului sau, altfel spus, raportul dintre variatia
relativa a cantitatii cerute ![]() si variatia relativa a pretului
si variatia relativa a pretului ![]() .
.
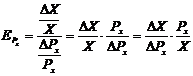 (4.8.),
(4.8.),
unde: EPx= coeficientul de elasticitate ‑ pret; X = variatia cantitatii cerute din bunul X; Px=variatia nivelului pretului bunului X.
Determinarea elasticitatii ‑ pret ridica insa unele probleme practice legate de intervalul de variatie pe care o calculam. Fixarea intervalului de variatie depinde, la randul ei, de natura bunului respectiv (daca este partial sau perfect divizibil, conform paragrafului 3.2.1.), cat si de informatiile legate de curba cererii (daca ii este sau nu cunoscuta functia matematica).
5.1.1. Elasticitatea 'arc'. Sa luam doua puncte, B si E de pe curba cererii trasata in fig. 4.6. realizata pe baza datelor din tab.
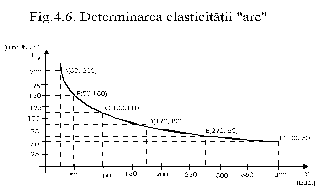
In felul acesta am ales o portiune sau un 'arc' al curbei. Pentru a determina elasticitatea pret a cererii cand trecem de la punctul E (care arata ca la pretul de 60 u.m. pe bucata se cer 270 bucati din bunul X) la punctul B (care arata ca atunci cand pretul se ridica la 150 u.m. cantitatea ceruta se reduce la 50 buc.), calculam coeficientul de elasticitate conform formulei (4.8.):
![]()
![]()
Acest coeficient rezulta
din faptul ca in timp ce pretul a crescut cu 150%, adica ![]() , cantitatea ceruta a scazut cu numai 81,48%, adica
, cantitatea ceruta a scazut cu numai 81,48%, adica ![]() . Deci, cantitatea ceruta s‑a modificat intr‑o
proportie mai mica decat pretul si in sens invers (de aici semnul '-'
din fata rezultatului), motiv pentru care putem afirma ca, in acest caz,
cererea este de elasticitate subunitara. Rezultatul va fi diferit cand vom trece
de la punctul E la punctul D
. Deci, cantitatea ceruta s‑a modificat intr‑o
proportie mai mica decat pretul si in sens invers (de aici semnul '-'
din fata rezultatului), motiv pentru care putem afirma ca, in acest caz,
cererea este de elasticitate subunitara. Rezultatul va fi diferit cand vom trece
de la punctul E la punctul D ![]() , la punctul C
, la punctul C ![]() , sau la punctul A
, sau la punctul A ![]() , cum este si firesc. Dar, algebric, - 1,11 sau - 1,47 sunt
mai mici decat 1, iar in realitate, cand trecem de la punctul E la punctul D
sau A variatia relativa a cantitatii cerute este mai mare decat variatia
relativa a pretului. Semnul '-' are doar semnificatia ca cele doua marimi
‑ cererea si pretul ‑ variaza in sens invers. Pentru a reflecta in
mod real raportul dintre variatiile relative ale celor doua marimi, vom calcula
coeficientul de elasticitate in valori absolute, punand in formula (4.8.)
semnul '-' intre paranteze (subliniind astfel caracterul conventional
al acestuia) in fata raportului, asa cum am procedat si la determinarea ratei
marginale de substituire de la 'teoria consumatorului':
, cum este si firesc. Dar, algebric, - 1,11 sau - 1,47 sunt
mai mici decat 1, iar in realitate, cand trecem de la punctul E la punctul D
sau A variatia relativa a cantitatii cerute este mai mare decat variatia
relativa a pretului. Semnul '-' are doar semnificatia ca cele doua marimi
‑ cererea si pretul ‑ variaza in sens invers. Pentru a reflecta in
mod real raportul dintre variatiile relative ale celor doua marimi, vom calcula
coeficientul de elasticitate in valori absolute, punand in formula (4.8.)
semnul '-' intre paranteze (subliniind astfel caracterul conventional
al acestuia) in fata raportului, asa cum am procedat si la determinarea ratei
marginale de substituire de la 'teoria consumatorului':
![]() (4.9.)
(4.9.)
In acest caz, rezultatul va fi mereu pozitiv, dar vom avea grija sa interpretam ca, atunci cand pretul se modifica cu un procent, cantitatea ceruta variaza in sens invers cu EPx ori mai mult.
In functie de valoarea calculata pentru coeficientul de elasticitate, EPx, exista urmatoarele situatii:
a) Daca EPx > 1, cererea este de elasticitate supraunitara, adica, la o modificare a pretului, modificarea cererii in sens invers este intr‑o proportie mai mare;
b) Daca EPx=1, cererea este de elasticitate unitara, adica, la o modificare a pretului, modificarea cererii in sens invers este in aceeasi proportie;
c) Daca EPx < 1, cererea este de elasticitate subunitara, adica, la o modificare a pretului, modificarea cererii in sens invers are loc intr‑o proportie mai mica.
Pot fi imaginate si doua cazuri extreme:
d) Daca EPx=0, spunem ca cererea este perfect inelastica, adica, oricat s‑ar modifica pretul, cantitatea ceruta ramane neschimbata sau variatia cererii este nula;
e) Daca EPx=, spunem ca cererea este perfect elastica, adica la o variatie infinit de mica a pretului, tinzand spre zero, cantitatea ceruta tinde sa creasca foarte mult.
In fig. 4.7. sunt reprezentate trei exemple de curbe ale cererii cu elasticitate constanta:
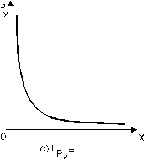
Curba cererii de elasticitate
unitara constanta. O crestere procentuala a pretului determina o scadere procentuala egala a cantitatii cerute in toate punctele curbei; curba este o hiperbola echilaterala. Produsul dintre pret si cantitatea ceruta sau consumata sau, altfel spus, cheltuielile consumatorului, raman constante, indiferent cum s‑ar modifica pretul,
Curba cererii perfect inelastice. Oricat de mult ar varia pretul, cantitatea ceruta sau consumata ramane neschimbata. Este dificil de gasit un astfel de bun in realitate, dar, intre anumite limite, determinate si de alti factori (in special venitul), produsele de stricta necesitate (de exemplu painea) se apropie de o astfel de reactie.
Curba cererii perfect elastice sau de elasticitate infinita. La foarte mici reduceri ale pretului cererea creste de la zero la infinit. Dincolo de pretul critic, consumatorii nu vor mai cumpara nimic. La nivelul pretului critic, ei vor cumpara tot ce gasesc (chiar si o cantitate infinita daca aceasta este disponibila).
Fig. 4.7. Curbe ale cererii cu elasticitate constanta
Calcularea elasticitatii 'arc' are avantajul ca se poate realiza foarte simplu. Informatia oferita despre reactia cererii la variatia pretului este insa incompleta. Stim ce se intampla cand trecem de la punctul E la punctele D, C, B sau A din fig. 4.6., mergand pe segmentele care le uneste de punctul initial in linie dreapta. Nu putem afla ce se intampla in fiecare punct al curbei cererii, ci stim doar ca elasticitatea este diferita.
In plus, coeficientul de
elasticitate va avea cu totul alta valoare daca in determinarea sa intre aceleasi
doua puncte vom schimba sensul de miscare. Astfel, de exemplu, atunci cand se
trece de la punctul B la E, daca vom lua in calcul X si Px ale
punctului B, ![]() , care este total diferit de 0,54, obtinut cand X si Px
au fost coordonate punctului E. Variatia absoluta intre aceste doua puncte a ramas
aceeasi, dar cea relativa este diferita, fiindca s‑a schimbat baza de
pornire. Inlaturarea acestui inconvenient poate fi realizata prin luarea in
calcul pentru X si Px nu a valorilor lor din punctul B sau E, ci a
mediilor aritmetice a acestora din cele doua puncte:
, care este total diferit de 0,54, obtinut cand X si Px
au fost coordonate punctului E. Variatia absoluta intre aceste doua puncte a ramas
aceeasi, dar cea relativa este diferita, fiindca s‑a schimbat baza de
pornire. Inlaturarea acestui inconvenient poate fi realizata prin luarea in
calcul pentru X si Px nu a valorilor lor din punctul B sau E, ci a
mediilor aritmetice a acestora din cele doua puncte:
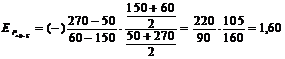
Putem retine deci si o alta formula de calcul a elasticitatii 'arc':
![]() (4.10)
(4.10)
5.1.2. Elasticitatea 'punct'. Pentru a inlatura neajunsurile determinarii elasticitatii 'arc' si in primul rand pentru a obtine informatii asupra elasticitatii cererii unui bun in functie de propriul pret in fiecare punct al curbei, daca se cunoaste ecuatia de cerere care descrie legatura functionala intre cantitatea ceruta si pret, se poate calcula elasticitatea 'punct'. A determina elasticitatea ‑ pret a cererii intr‑un punct inseamna a calcula variatia relativa a lui X pentru o variatie atat de mica a pretului (care tinde spre zero) incat, practic, ramanem in acelasi punct de pe curba cererii. Pentru aceasta se calculeaza derivata lui X in raport cu Px, astfel incat in formula (4.9) inlocuim 'X/Px' cu 'X/Px' si obtinem:
![]() (4.11),
(4.11),
A fiind oricare din punctele curbei in care dorim sa determinam elasticitatea.
Revenind la ecuatia cererii liniare din paragraful 1.2., X = -Px+12, reprezentata in fig. 4.2., elasticitatea 'punct' a cererii fata de pret in punctul A de coordonate (2,10) este:
![]()
![]()
Deci, in punctul A, la o variatie a pretului, cantitatea ceruta variaza in sens invers de 5 ori mai mult. Cererea in acest punct este de elasticitate supraunitara. In punctul B de coordonate (10,2) din fig. 4.2.,
![]()
Cererea in punctul B este de elasticitate subunitara.
Cunoscand, pe baza studiilor empirice de pe piata, coeficientii de elasticitate a cererii pentru diverse bunuri, in functie de diferitele niveluri ale preturilor lor, agentii economici isi vor putea fundamenta mai bine strategiile lor cu privire la preturile practicate, pentru a‑si realiza obiectivele legate de cantitatile aduse spre desfacere.
5.2. Elasticitatea-pret incrucisata
La fel de importanta pentru cunoasterea pietei de catre agentii economici este si reactia cererii pentru un anumit bun in functie de variatiile preturilor altor bunuri si servicii. Studierea acesteia se realizeaza cu ajutorul elasticitatii incrucisate.
Elasticitatea-pret incrucisata exprima, deci, gradul de sensibilitate a consumului sau cererii pentru un bun X in functie de variatia pretului altui bun, Y, calculandu‑se ca raport intre modificarea relativa a cantitatii cerute din primul bun, X/X, si modificarea relativa a pretului celuilalt bun, Py/Py. Similar cu calculul elasticitatii pret directe, vom determina un coeficient al elasticitatii incrucisate potrivit formulei:
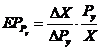 (4.12)
(4.12)
sau cu ajutorul derivatei, atunci cand cunoastem functia completa a cererii:
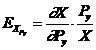 (4.13.)
(4.13.)
Exista mai multe cazuri,
in functie de valoarea pe care o ia ![]() :
:
a) Daca ![]() = 0, bunurile X si Y sunt independente, adica o
variatie a pretului lui U nu are nici un efect asupra consumului bunului X. De
exemplu, modificarea pretului casetelor audio nu are nici o influenta asupra
cantitatii cerute din produsul paine.
= 0, bunurile X si Y sunt independente, adica o
variatie a pretului lui U nu are nici un efect asupra consumului bunului X. De
exemplu, modificarea pretului casetelor audio nu are nici o influenta asupra
cantitatii cerute din produsul paine.
b) Daca ![]() este pozitiv si
subunitar (()<
este pozitiv si
subunitar (()<![]() <1), cele doua bunuri sunt substituibile, adica o
crestere a pretului lui Y il determina pe consumator sa‑si diminueze
cantitatea ceruta si consumata din acest bun (conform primei legi a cererii), crescand in schimb cantitatea ceruta
din bunul X, care poate satisface si el aceeasi nevoie pentru a carei acoperire
era consumat Y. Altfel spus, ca urmare a cresterii pretului bunului Y,
consumatorul il subsitituie cu un alt bun, X. Deci, creste pretul lui Y, creste
si consumul lui X. Variatia pretului lui Y si a cantitatii lui X este de acelasi
sens. Raportul acestor doua variatii de acelasi sens este pozitiv. De exemplu,
daca sporeste pretul untului, consumatorul il va inlocui cu margarina. Untul si
margarina sunt bunuri substituibile; la fel ca si transportul auto si cel
feroviar etc.
<1), cele doua bunuri sunt substituibile, adica o
crestere a pretului lui Y il determina pe consumator sa‑si diminueze
cantitatea ceruta si consumata din acest bun (conform primei legi a cererii), crescand in schimb cantitatea ceruta
din bunul X, care poate satisface si el aceeasi nevoie pentru a carei acoperire
era consumat Y. Altfel spus, ca urmare a cresterii pretului bunului Y,
consumatorul il subsitituie cu un alt bun, X. Deci, creste pretul lui Y, creste
si consumul lui X. Variatia pretului lui Y si a cantitatii lui X este de acelasi
sens. Raportul acestor doua variatii de acelasi sens este pozitiv. De exemplu,
daca sporeste pretul untului, consumatorul il va inlocui cu margarina. Untul si
margarina sunt bunuri substituibile; la fel ca si transportul auto si cel
feroviar etc.
c) Daca ![]() este pozitiv si
supraunitar, (EXPy>1), bunurile X si Y sunt strans substituibile,
cantitatea ceruta din X crescand intr‑o proportie mai mare decat cea a
majorarii pretului lui Y;
este pozitiv si
supraunitar, (EXPy>1), bunurile X si Y sunt strans substituibile,
cantitatea ceruta din X crescand intr‑o proportie mai mare decat cea a
majorarii pretului lui Y;
d) Daca - 1 < ![]() < 0, aceasta inseamna ca la o crestere a pretului bunului
Y, cantitatea ceruta din bunul X se va diminua, intr‑o proportie insa mai
mica decat cea a majorarii pretului celuilalt bun. Bunurile X si Y in acest caz
sunt complementare
sau fac pereche in consumul individului. De exemplu, benzina si automobilul: o
crestere a pretului benzinei, fara de care automobilul nu poate circula, va
determina o reducere a cantitatii cerute de benzina si o diminuare a cererii de
automobile.
< 0, aceasta inseamna ca la o crestere a pretului bunului
Y, cantitatea ceruta din bunul X se va diminua, intr‑o proportie insa mai
mica decat cea a majorarii pretului celuilalt bun. Bunurile X si Y in acest caz
sunt complementare
sau fac pereche in consumul individului. De exemplu, benzina si automobilul: o
crestere a pretului benzinei, fara de care automobilul nu poate circula, va
determina o reducere a cantitatii cerute de benzina si o diminuare a cererii de
automobile.
e) Daca ![]() este negativ si mai
mic decat -1 (deci
este negativ si mai
mic decat -1 (deci ![]() <-1), bunurile X si Y sunt strans complementare: o
crestere a pretului bunului Y provoaca o reducere intr‑o proportie mai
mare a cantitatii cerute.
<-1), bunurile X si Y sunt strans complementare: o
crestere a pretului bunului Y provoaca o reducere intr‑o proportie mai
mare a cantitatii cerute.
Daca reluam ecuatia completa a cererii (4.5.), atunci cand Py = 10 iar X = 25, vom calcula elasticitatea-pret incrucisata astfel (vezi relatia 4.13.):
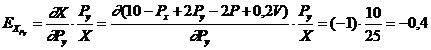
In acest exemplu, bunurile X si Y sunt complementare: la o crestere a pretului lui Y cantitatea ceruta din X se diminueaza intr‑o proportie mai mica decat modificarea pretului celuilalt bun.