
|
|
|
Proiect didactic
Unitatea de invatamant: Grup Scolar Industrial Transporturi Cai Ferate Galati
Data: 03.12.
Clasa: a X-a (Matematica - Informatica)
Disciplina: Matematica
Unitatea de invatare: Functii si ecuatii
Subiectul lectiei: Ecuatii exponentiale
Tipul lectiei: Mixta
Durata lectiei: 50 de minute
Locul de desfasurare: Sala de clasa
Competente specifice:
Trasarea prin puncte a graficelor unor functii
- Prelucrarea informatiilor ilustrate prin graficul unei functii in scopul deducerii unor proprietati ale acesteia (monotonie, semn, bijectivitate, inversabilitate, continuitate, convexitate).
Utilizarea de proprietati ale functiilor in trasarea graficelor si rezolvarea de ecuatii.
Competente derivate (Obiective operationale):
C1 Utilizarea proprietatilor functiei exponentiale
C2 Rezolvarea ecuatiilor exponentiale folosind injectivitatea functiei exponentiale
C3 Rezolvarea ecuatiilor exponentiale folosind metoda substitutiei
C4 Rezolvarea ecuatiilor exponentiale folosind metode combinate
Strategia educationala:
- metode si procedee: conversatia, explicatia, demonstratia, exercitiul, problematizarea
- forme de organizare: frontala, individuala
- mijloace de invatamant: manualul, fise de lucru
Bibliografie :
1. C. Udriste (coord.), Matematica, Manual pentru clasa a X-a, Editura Fair Partners, Bucuresti, 2005.
2. ***, Fise cu probleme din arhiva personala
Anexe: Schema pe tabla, fise de lucru
|
Momentele lectiei |
Competente derivate |
Continutul informational al lectiei |
Strategia educationala |
|||
|
Activitatea profesorului |
Activitatea elevilor |
Metode si procedee |
Mijloace de invatamant |
Forme de Organizare |
||
|
Moment organizatoric (2') |
|
Verifica prezenta elevilor. Verifica existenta resurselor materiale. |
Raspund la intrebari. |
Conversatia |
|
Frontala |
|
Verificarea cunostintelor anterioare (8') |
C1 |
Verifica tema prin sondaj. Reactualizeaza notiunea de functie exponentiala si proprietatile acesteia. |
Raspund la intrebari. |
Conversatia Exercitiul |
Manual |
Frontala |
|
Anuntarea temei si a obiectivelor (2') |
|
Anunta tema, obiectivele lectiei si scrie titlul lectiei pe tabla. |
Noteaza titlul lectiei pe caiete. |
Explicatia |
|
Frontala |
|
Predarea - invatarea noilor cunostinte (20') |
C1, C2, C3, C4 |
Prezinta notiunile noi. Explica modul de rezolvare pentru diferite tipuri de ecuatii exponentiale. Care sunt proprietatile functiei exponentiale folosite in rezolvare? Ilustreaza fiecare tip de ecuatie prin exemple. |
Urmaresc prezentarea si iau notite. Raspund intrebarilor profesorului. |
Conversatia Explicatia Demonstratia Exercitiul |
Manual |
Frontala |
|
Fixarea cunostintelor (15') |
C1, C2, C3, C4 |
Distribuie fisele de lucru. Discuta modul de rezolvare a aplicatiilor din fisa. Apreciaza prin note raspunsurile primite. |
Analizeaza fisele de lucru. Raspund la intrebarile profesorului. Rezolva exercitiile si comunica rezultatele. |
Explicatia, conversatia euristica, exercitiul, problematizarea |
Fise de lucru |
Individuala Frontala |
|
Tema pentru acasa (3') |
|
Anunta tema pentru acasa si da indicatii privind modul de rezolvare. |
Noteaza tema. Sunt atenti la indicatii. |
Explicatia |
Manual Fise de lucru |
Frontala |
Anexa 1
Schema pe tabla
Verificarea cunostintelor anterioare
Se rezolva la tabla:
Sa se stabileasca monotonia functiilor: ![]() definite prin:
definite prin:
a)![]() ; b)
; b) 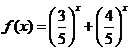 .
.
Rezolvare.
a) Functia![]() este strict crescatoare fiind suma a doua
functii strict crescatoare:
este strict crescatoare fiind suma a doua
functii strict crescatoare:
![]() si
si ![]() . (Exponentiala cu baza supraunitara este
strict crescatoare.)
. (Exponentiala cu baza supraunitara este
strict crescatoare.)
b) Functia ![]() este strict descrescatoare
fiind suma a doua functii strict descrescatoare:
este strict descrescatoare
fiind suma a doua functii strict descrescatoare:
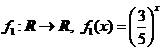 si
si 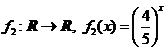 . (Exponentiala cu baza subunitara este strict
descrescatoare.)
. (Exponentiala cu baza subunitara este strict
descrescatoare.)
Predarea - invatarea noilor cunostinte
Intr-o definire neformala, o ecuatie exponentiala este o ecuatie in care necunoscuta apare numai la exponent.
Tipuri de ecuatii exponentiale
1. Ecuatii exponentiale de forma ![]() ,
, ![]() ,
, ![]()
Rezolvare. In baza
injectivitatii functiei exponentiale, ecuatia este
echivalenta cu ecuatia ![]() .
.
Exemplu. 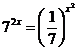
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]() .
.
2. Ecuatii exponentiale de forma ![]() ,
, ![]() ,
, ![]()
Rezolvare. Notam ![]() .
.
Daca ![]() ecuatia
ecuatia ![]() nu are solutii
(deoarece exponentiala ia numai valori pozitive).
nu are solutii
(deoarece exponentiala ia numai valori pozitive).
In cazul ![]() , in baza bijectivitatii functiei
exponentiale (considerata cu codomeniul
, in baza bijectivitatii functiei
exponentiale (considerata cu codomeniul ![]() ), ecuatia
), ecuatia ![]() are solutie unica
are solutie unica ![]() . Rezolvarea ecuatiei initiale se reduce astfel la
ecuatia
. Rezolvarea ecuatiei initiale se reduce astfel la
ecuatia ![]() .
.
Exemple. a) Ecuatia ![]() nu are solutie.
nu are solutie.
b) ![]()
![]()
![]() .
.
c) ![]()
![]()
![]()
![]()
![]()
![]()
![]() care are solutiile
care are solutiile ![]() si
si ![]() .
.
d) ![]()
![]()
![]()
![]()
![]()
![]()
![]() care nu are
solutii reale.
care nu are
solutii reale.
Observatie. In cazul ![]() , ecuatiile de tipul 2 sunt cazuri particulare de
ecuatii de tip 1. Luam
, ecuatiile de tipul 2 sunt cazuri particulare de
ecuatii de tip 1. Luam ![]() .
.
3. Ecuatii exponentiale de forma ![]() ,
, ![]() ,
, ![]()
Rezolvare. Se noteaza ![]() si se obtine ecuatia:
si se obtine ecuatia: ![]() .
.
Exemplu. ![]()
Notam ![]() . Obtinem ecuatia
. Obtinem ecuatia ![]() , cu solutiile
, cu solutiile ![]() si
si ![]() . Revenind la substitutia facuta,
. Revenind la substitutia facuta,
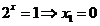
![]()
4. Ecuatii exponentiale cu solutie unica
Rezolvare. Ecuatia se aduce
la forma ![]() , unde
, unde ![]() este o functie strict monotona, iar
este o functie strict monotona, iar ![]() o constanta. Se gaseste
prin observatie directa o solutie
o constanta. Se gaseste
prin observatie directa o solutie ![]() a ecuatiei,
solutie care este unica datorita injectivitatii lui
a ecuatiei,
solutie care este unica datorita injectivitatii lui ![]() .
.
Exemplu. ![]()
![]()
![]() care are solutia
care are solutia ![]() . Cum functia
. Cum functia ![]() ,
, ![]() este strict
crescatoare (ca suma de functii strict crescatoare)
rezulta ca
este strict
crescatoare (ca suma de functii strict crescatoare)
rezulta ca ![]() este injectiva, deci
este injectiva, deci ![]() este unica
solutie a ecuatiei date.
este unica
solutie a ecuatiei date.
Fixarea noilor cunostinte
Elevii vor rezolva urmatoarele exercitii din fisa de lucru, precizand mai intai tipul fiecarei ecuatii: 1c, 1e, 2a, 2g.
Tema pentru acasa: Ex.1: a, b, d, f, g , Ex.2: b, d, e, f din fisa.
Anexa 2
Fisa de lucru
Ecuatii exponentiale - Clasa a X-a
1. Sa se rezolve:
a) ![]() ; b)
; b) 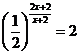 ; c)
; c) 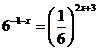 ;d)
;d) 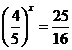 ;
;
e) ![]() ; f)
; f) ![]() ; g)
; g) ![]() .
.
2. Sa se rezolve:
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ; d)
; d) ![]() ;
;
e) ![]() ; f)
; f) 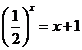 ; g)
; g) ![]() .
.