|
|
|
Inca de la aparitie, in 1930, teoria orbitalelor moleculare s-a dovedit a fi un instrument important in interpretarea proprietatilor fizice si chimice ale moleculelor. Aceasta teorie considera moleculele ca fiind entitati noi; spre deosebire de teoria mai veche a legaturii de valenta (Valence Bond) in teoria orbitalelor moleculare atomii care formeaza molecula isi pierd individualitatea, interpatrunderea orbitalelor atomice conducand la formarea unor orbitale moleculare proprii moleculelor.
Orbitalele moleculare sunt solutii ale ecuatiei lui Schrödinger (I.16). Rezolvarea exacta a acestei ecuatii nu poate fi facuta decat in cazurile sistemelor monoelectronice , deci in cazul atomilor hidrogenoizi si a moleculei ionice de hidrogen.
Existenta termenului de repulsie electronica in expresia hamiltonianului unei molecule polielectronice (vezi aplicatia 3) face imposibila scrierea operatorului H ca o suma de operatori monoelectronici si separarea ecuatiei (I.16) in n ecuatii monoelectronice rezolvabile exact. In consecinta rezolvarea ecuatiei se va face prin cautarea unor solutii aproximative.
Se pune problema de ce forma vor fi aceste solutii aproximative; una din aproximatiile folosite este aceea cunoscuta sub numele de aproximatia orbitala sau modelul particulelor independente si implica scrierea functiei de starea a
sistemului 
ca un produs de functii monoelectronice 
(i, µ = 1,n)
solutii ale unui hamiltonian monoelectronic efectiv care include, intr-o
forma neexplicita, intreaga energie potentiala a
electronului µ in interactie cu nucleul si cei n-1
electroni:
(I.22)
Acest produs, denumit si produs Hartree, nu poate fi forma adecvata a functiei de stare deoarece tine seama numai de semnificatia de densitate de probabilitate a modulului functiei asociat unor particule independente, dar nu tine cont de :
existenta spinului electronului
caracterul indiscernabil al electronilor care conduce la degenerarea de permutare
caracterul antisimetric al functiei (sa schimbe semnul la permutarea a doi electroni) cerut de principiul lui Pauli (in formularea cuanto-mecanica) pentru ansambluri de fermioni (particule cu spinul semiintreg)
Introducerea acestor trei cerinte se
face prin asocierea fiecarei
orbitale moleculare a unei functii de
spin 
(notate generic cu 
), orbitala moleculara fiind inlocuita cu o spin
orbitala de tipul 
. Cei n electroni vor ocupa n spin orbitale obtinute din
n/2 orbitale moleculare. Antisimetria se realizeaza prin scrierea
functiei sub forma unui determinant, numit determinant Slater, ale
carui elemente sunt cele n spin orbitale asociate celor n electroni, deci
sub forma unei combinatii liniare de produse de spin orbitale:
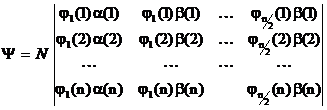(I.23)
Functia (I.23) corespunde unei configuratii de strat inchis, fiecare din cele n/2 orbitale moleculare fiind dublu ocupate. Factorul N reprezinta constanta de normare.
Pentru determinantul Slater
corespunzator functiei totale 
numarul asociat
electronului reprezinta indicele de linie, iar numarul spin
orbitalului indicele de coloana.
Functia va fi
antisimetrica deoarece, dupa cum se stie, permutarea a doua
linii, corespunzatoare permutarii a doi electroni, schimba
semnul determinantului. Existenta a doua coloane identice conduce la
anularea determinantului, deci din punct de vedere fizic este imposibil ca doi
electroni sa ocupe aceeasi spin orbitala (sa aiba acelasi
spin), ceea ce corespunde unei formulari echivalente a principiului lui
Pauli: intr-o orbitala moleculara nu pot exista decat doi electroni
de spin opus.
In principiu, pentru o configuratie
data, functia de unda a unui sistem polielectronic poate fi
scris sub forma unui determinant sau a unei combinatii de
determinanti Slater, atata timp cat se cunosc orbitalele moleculare
spatiale 
.
Pentru aproximarea acestor orbitale, in
teoria orbitalelor moleculare, a fost introdusa aproximatia LCAO (Linear
Combination of Atomic Orbitals).
Potrivit acestei aproximatii orbitala moleculara se poate scrie ca o
combinatie liniara de orbitale atomice 
, fiecare atom putand participa cu una sau mai multe orbitale
atomice (OA), aproximatie justificata prin faptul ca orbitalele
moleculare provin din OA:
(I.24)
in care 
este orbitala
atomica m a atomului A.
Relatia (I.24) poate fi scrisa intr-o forma mai restransa:
(I.25)
unde insumarea se face dupa orbitalele tuturor
atomilor (
).
In
final problema consta in a gasi coeficientii 
(
) care sa conduca la o solutie cat mai
apropiata de solutia reala. Pentru aceasta se aplica metoda
variationala care are la baza
principiul de minimizare a energiei prin gasirea unei solutii
adecvate.
Diferitele metode aparute in cadrul teoriei orbitalelor moleculare, apeleaza intr-un fel sau altul, in functie de gradul de sofisticare al metodei, odata cu cresterea acuratetii cu care se determina solutiile, la metoda variationala.
Metoda variationala are la baza inegalitatea :
(I.26)
in care 
reprezinta o
functie de incercare, iar E este o valoare proprie operatoru-lui H si
corespunde energiei sistemului.
Daca
functia ar fi functie
proprie operatorului H, atunci, conform ecuatiei
(I.16), integrala I ar fi egala cu 0 si inegalitatea (I.26) ar deveni
egalitate. In consecinta, va trebui gasita acea functie
care sa
minimizeze integrala I. Functia de incercare se scrie ca o combinatie
liniara de functii cunoscute
liniar independente de tipul celei date de relatia (I.25) si va fi o functie
de parametrii (); integrala I devine:
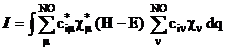(I.27)
Relatia (I.27) se poate scrie:
(I.28)
Cu urmatoarele notatii:
ecuatia (I.28) devine:
(I.29)
unde 
reprezinta
elementele de matrice ale operatorului H,
iar 
reprezinta fie
conditia de normare cand 
, fie integrala de acoperire pentru 
.
Se
pune apoi conditia ca integrala I sa ia o valoare minima in raport cu
parametrii 
:
pentru (I.30)
Se
obtine in acest fel un sistem de NO ecuatii liniar omogene cu NO
necunoscute ():
(I.31)
Pentru
ca sistemul (I.31) sa admita si alte solutii in afara celei
banale (
) trebuie ca determinantul sau secular sa fie egal cu
zero:
(I.32)
Ecuatia
(I.32) este de gradul NO in E. Prin rezolvarea acestei ecuatii se
obtin cele NO radacini: 
. Cea mai mica dintre ele reprezinta valoarea aproximativa
a energiei reale a sistemului.
Cunoscand
radacinile ecuatiei seculare se pot determina
radacinile sistemului de ecuatii (I.31); acesta este compatibil
dar nedeterminat. Coeficientii 
se obtin in
raport cu unul dintre ei. Prin adaugarea conditiei de normare
acestia sunt determinati si in acest fel se obtin NO seturi
de coeficienti (
) care vor defini NO functii de stare de forma (I.25).
(I.33)
In cadrul teoriei orbitalelor moleculare au aparut o serie de metode de calcul care se deosebesc prin:
setul de orbitale atomice folosite, corespunzatoare fiecarui atom:
set
restrans: OA de tip 
;
set de valenta: OA corespunzatoare stratului de valenta (ex: 2s 2p);
set minimal: set de valenta plus OA interioare;
set extins: set minimal plus straturi exterioare;
tipul OA folosite:
Hartree-Fock
Slater
Combinatii de OA de tip gaussian
forma hamiltonianului;
numarul
si tipul integralelor neglijate din expresia elementelor de matrice ale
hamiltonianului: exceptand metodele ab
initio care calculeaza toate integralele, celelalte se bazeaza pe
neglijarea totala sau partiala a acoperirii diferentiale (ZDO: 
)
gradul de folosire a unor date experimentale in evaluare integralelor ce intervin in calcul:
metode empirice care egaleaza integralele cu parametrii empirici avand in vedere semnificatia fizica a acestora:
Hückel
tehnica
Wheland
Del Re
metode semiempirice care calculeaza anumite integrale, iar pe altele le egaleaza cu parametrii empirici:
SCF-PPP
Hückel generalizata (Extended Hückel)
CNDO, INDO, MINDO, MNDO, ZINDO, PM3,AM1
pachetele de programe MOPAC, AMPAC si AMSOL
metode care calculeaza toate integralele, asa numitele metode ab initio:
pachetul de programe Gaussian
pachetul de programe GAMESS (General Atomic and Molecular Electronic Structure System
