Conditii de inscriere geometrica in curbe

Conditii de inscriere geometrica in curbe

Problema inscrierii in curbe a unui vehicul de cale ferata are ca scop esential stabilirea conditiilor in care un vehicul poate, in anumite conditii, sa circule printr-o curba determinata fara a deraia. Legat de aceasta apar si alte aspecte, ca de exernplu acela de mentinere a vehiculului in spatiul impus de gabarit.

Inscrierea materiala a vehiculului intr-o curba are in primul rand un aspect pur geometric, aceasta depinzand de dimensiunile vehiculului si cele ale caii de rulare.

Din punctul de vedere al ghidarii, prin vehicul se intelege un ansamblu format din una sau mai multe osii legate printr-un sasiu. Dupa modul de legare al osiilor in sasiu se deosebesc doua categorii de vehicule:

-cu osii fixe - la care osiile raman tot timpul paralele si perpendiculare pe axa longitudinala de simetrie a sasiului; osiile nu se pot deplasa longitudinal fata de sasiu, dar se pot deplasa transversal in limitele jocurilor admise; marea majoritate a vehiculelor actuale sunt cu osii fixe;

-cu osii orientabile - la care pe langa deplasarea transversala este posibila si rotirea osiilor fata de sasiu; aceasta miscare de rotatie, dependenta de jocurile longitudinale de la cutiile de osii, da posibilitatea osiei de a se dispune radial in curbe, ceea ce are ca efect o reducere importanta a uzurilor suprafetelor de rulare si a buzelor, respectiv ale flancurilor de sine.

Asezarea unui vehicul cu buzele rotilor intre cele doua fire ale caii este asigurata de largimea canaluii de ghidare, adica de existenta jocului total intre buza si flancul interior al sinei (fig...).

Daca osia este dispusa radial in curba, jocul definit conventional este σ = E E₀, care se considera de catre proiectantii de vehicule, pentru situatia cea mai defavorabila, la valoarea sa minima, adica pentru ecartamentul caii E la valoarea minima (1432 + S mm,) si pentru ecartamentul osiei E_Q la valoarea maxima (1426 mm).

Jocul normal al osiei in cale este σ = 1435 - 1426 - 9 mm . Daca se tine seama de faptul ca ecartamentul caii se masoara la 14 mm sub nivelul superior al sinelor, valoarea lui σ este ceva mai mare. La studiul inscrierii in curbe a vehiculelor se utilizeaza in general σ = 10 mm, la care se adauga valoarea supralargirii caii in curba.

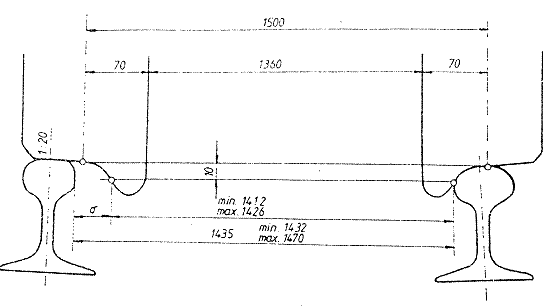
Fig.Jocul total intre buza si flancul interior al sinei la osia in pozitie normala fata de firele caii

Daca osia este in pozitie de atac, cu un unghi  α fata de cale, la rotile obisnuite, jocul se va micsora, deoarece prin rotirea osiei se ingusteaza canalul de ghidare. Dar la rotile cu diametru mic este posibila chiar marirea jocului cand osia este in pozitie de atac.

Planul cercutui

| nominal de rulare

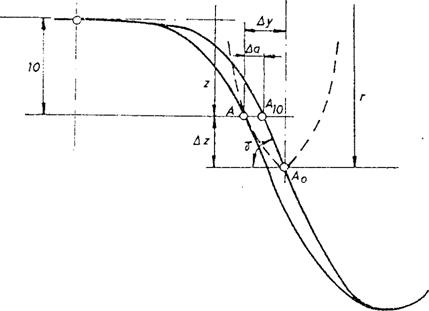
Fig..Decalajele punctului A ' fata de A₀

Dupa cum se vede in fig. ..pe profilul aparent al rotii, la cota de 10 mm sub cercul nominal de rulare se afla punctul A `, care este situat totodata si pe elipsa aparenta cu varful in punctul A<sub>0</sub> de pe profilul normal al rotii. Punctul A` este decalat fata de A₀ :

transversal, cu Δy - e cos α = b sin α = r sin α tg α

vertical, cu Δz = r - z = r (√ 1 - tg ²α tg ²γ )

Tinand seama ca unghiul de atac este mic, se poate considera sin α = α

cos α = 1 si, prin urmare,

Δy = r α² tg γ ;

Decalajul transversal al punctului A ` fata de punctul A_l0 este

Δa = Δ y - Δz ctg γ = (1/2) r α² tg γ

Punctul A` reprezinta proiectia pe planul vertical normal pe firele caii a punctu­lui A_a (decalat longitudinal cu b_a = rα tg γ fata de planul meridian vertical al osiei) situat pe profilul rotii, respectiv pe curba C (fig. 3.3) care reprezinta conturul sectiunii obtinute prin intersectia rotii cu planul orizontal ce trece prin A_l0 . Tangenta in punctul A_a la curba C face unghiul α cu un plan paralel al rotii

Daca se noteaza cu E₀ α distanta dintre punctele A_a  corespunzatoare celor doua roti ale osiei, atunci abaterea de la ecartamentul E₀ al osiei va fi

Δσ = E _α0 - E ₀

unde, conform fig. .

E _α0 = 2 Δ a + E₀ cos α

si deci

Δσ = 2 Δ a - E₀ (1- cos α)  = 2 Δ a - E₀ sin² (α/2)

care, dupa inlocuiri, devine   

Δσ  = α ²( r tg γ - E₀/2)

Rezulta ca jocul σ, pentru situatia pozitiei de atac a osiei, va fi

σ = E - E₀ - Δσ

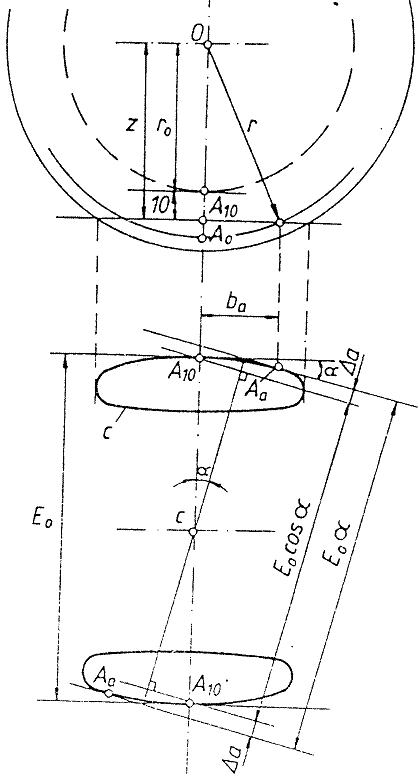
Fig.. Modificarea jocului la rotirea cu unghiul α a osiei

Avand in vedere valorile mici ale abaterii   Δσ care rezulta pentru valorile uzuaie ale lui r, α, si γ in calculele practice aceasta poate fi neglijata. Asa cum s-a aratat, determinarea latimii canalului de ghidare se bazeaza pe consideratia conventionala ca punctul de contact al buzei cu flancul interior al sinei se afla la cota de 10 mm sub cercul nominal de rulare. O analiza riguroasa a acestei probleme implica determinarea punctelor reale de contact care tine seama de profilul rotii si al sinei.

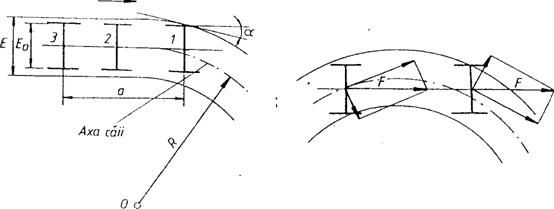
Fig.Atacarea curbei de catre vehicul.           Fig. ..Influenta fortei de tractiune F asupra   asezarii vehiculului in cale

Si la mersul in aliniament, datorita miscarii de serpuire, osia se poate situa in pozitie de atac fata de cale iar consumarea jocurilor este posibila datorita miscarilor transversale ale osiilor.

La atacarea unei curbe (fig...), osia 1 a vehiculului realizeaza in permanent contactul buzei cu flancul interior al sinei de pe firul exterior al caii.

Asezarea vehiculului in cale este determinata de fortele care actioneaza asupra acestuia. Astfel, se considera ca asupra unui vehicul care circula intr-o curba actioneaza numai o forta de tractiune F orientata de-a lungul axei sale longitudinale (fig...). Descompunand la fiecare osie forta F dupa doua directii, una tangentiala si cealalta normala pe firele caii, se constata ca forta normala obliga prima osie sa atace firul exterior al caii iar pe ultima sa se deplaseze spre firul interior pana cand, daca jocul in cale permite, aceasta sa se dispuna in pozitie radiala si astfel componenta normala a fortei F sa se anuleze.

Pentru studiul inscrierii geometrice in curba a unui vehicul cu osii fixe este suficient sa se reprezinte numai canalul de ghidare al caii, adica cele doua fire de cale distantate cu jocul σ , iar vehiculul redus la axa sa longitudinala. Pozitiile osiilor sunt marcate prin puncte pe axa longitudinala a vehiculului, punctul care reprezinta prima osie aflandu-se intotdeauna pe firul exterior al caii.

Piciorul Ω al perpendicularei duse din centrul de curbura al caii pe axa longitudinala a vehiculului poarta  numele de pol iar perpendiculara - axa polara. Distanta de la prima osie la polul Ω se nume§te distanta. polara. Daca polul Ω coincide cu punctul de pe axa vehiculului corespunzator unei osii. atunci osia respectiva se va afla in pozitie radiala.

Daca osiile extreme se afla pe firul exterior al caii iar cele intermediare in interiorul canalului de ghidare, se spune ca vehiculul s-a inscris geometric in curba.