
|
|
|
indicatori de fiabilitate
INDICATORII DE FIABILITATE sunt marimi caracteristice care
permit aprecierea cantitativa a nivelului de fiabilitate al
dispozitivelor.
Indicatorii de fiabilitate se pot referi la intreaga populatie de dispozitive sau la un esantion prelevat dintr-o populatie de dispozitive.
Populatia este orice multime de
dispozitive similare, avand proprietati comune care este
supusa unui studiu statistic.
ESANTIONUL este un grup de dispozitive selectat
aleator dintr-o multime de dispozitive similare, care formeaza o populatie
Organizarea esantioanelor
Reprezentativitatea esantionului
Eficienta economica
Nivel de incredere in rezultate
Capacitatea de preluare si prelucrare a informatiei
Inregistrarea defectiunilor
![]()
![]() Inregistrarea
defectiunilor eveniment cu eveniment
Inregistrarea
defectiunilor eveniment cu eveniment
pe subintervale de observare
Se inregistreaza momentele in care se produc defectiunile;
Se retin valorile extreme;
Se calculeaza marimea unui subinterval de observare:
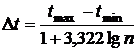
, marimea teoretica;
se aleg t min, t max si Dt , de preferinta numere naturale, astfel incat numarul subintervalelor de observare sa fie natural:
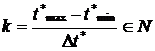
2.1 INDICATORI DE FIABILITATE AI DISPOZITIVELOR NEREPARABILE
Dispozitive nereparabile - odata defectate se inlocuiesc, neputand fi reparate.
Ex.: becuri, bujii, curele de transmisie, garnituri de etansare, segmenti etc.
2.1.1 Functia de fiabilitate, R(t)
FUNCTIA DE FIABILITATE - probabilitatea ca la
momentul considerat, t, un dispozitiv, aflat in conditii date
de utilizare, sa-si indeplineasca functiunile
specifice. - probabilitatea ca momentul T,
la care se produce defectiunea, sa fie mai mare decat momentul
curent, t.
![]()
![]()
(in limba engleza Reliability
unde: N(t) este numarul dispozitivelor aflate in buna stare de functionare la momentul t;
N0 - numarul dispozitivelor din care a fost alcatuit initial esantionul supus observatiei.
In cazul studiilor statistice,
![]()
; pentru t = 0, R(0) = 1;
pentru t , R( = 0/N0 = 0.
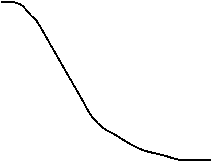
R(t) R(t)
![]()
![]()
![]()
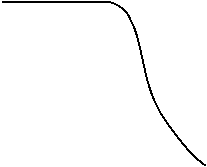
![]() 1 1
1 1
dispozitive cu
rezerva mare
de viata
![]()
![]() 0 t 0 t
0 t 0 t
Functia de fiabilitate permite:
aprecierea nivelului de incredere in utilizarea unui dispozitiv la un anumit moment t din viata sa;
compararea nivelului de fiabilitate al unor dispozitive realizate de producatori diferiti;
compararea conditiilor de utilizare ale unor dispozitive realizate de acelasi producator, dar aflate la utilizatori diferiti.
2.1.2 Functia de defectare (de repartitie), F(t)
FUNCTIA
DE DEFECTARE - probabilitatea ca momentul T,
la care se produce defectiunea, sa fie mai mic decat momentul
curent, t.
![]()
(in limba engleza Failure
(in limba engleza Failure
unde: n(t) este numarul dispozitivelor care s-au defectat pana in momentul t.
In cazul studiilor statistice
![]()
![]()
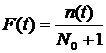
. Daca N0 < 20, atunci:
In cazul inregistrarii defectelor pe subintervale de observatie:
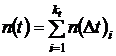 ,
unde n(t)i este numarul dispozitivelor
defectate in subintervalul (t)i ; kt - numarul subintervalelor pana
la momentul t.
,
unde n(t)i este numarul dispozitivelor
defectate in subintervalul (t)i ; kt - numarul subintervalelor pana
la momentul t.
Proprietati
t = 0, n(0) = 0; T F(0) = 0;
t , n = N0 T F(∞ = 1.
F(t) + R(t) = 1
Deoarece
n(t) + N(t) = N0 T
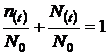 ,
sau
,
sau
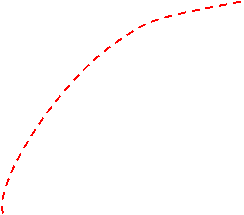
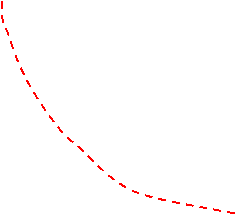
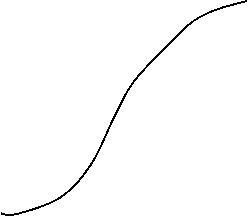
![]() R(t), F(t)
R(t), F(t)
![]()
 1
1
![]()
F(t)
![]() 0,5
0,5
![]()
 R(t)
R(t)
![]() 0
0
t
OBSERVATIE R(t) si F(t) descriu comportarea
dispozitivelor din punct de vedere al producerii defectiunilor pe un interval de timp [0, t]
2.1.3 Densitatea de probabilitate a timpului de buna functionare (frecventa relativa a defectiunilor, densitatea defectiunilor), f(t)
Densitatea de
probabilitate a timpului de buna functionare reprezinta limita
raportului dintre probabilitatea ca un dispozitiv sa se defecteze in
intervalul inchis la stanga [t - Dt, t si marimea intervalului Dt atunci cand aceasta din
urma tinde catre 0.
![]()
Statistic reprezinta raportul dintre
numarul de defectiuni ce apar in unitatea de timp pe parcursul
unui subinterval si numarul de dispozitive luate initial in
observare.
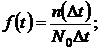
n(t) = N(t - t) - N(t);
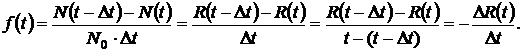
Daca ![]() 0, atunci
0, atunci
Deoarece R(t) = 1 - F(t), rezulta:
![]()
Deci f(t) reprezinta viteza de defectare a dispozitivelor.
Conform ultimei relatii, f(t) dt = dF(t); rezulta:
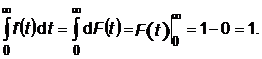
![]()
![]()
![]()
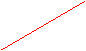
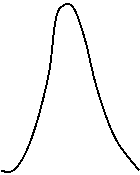
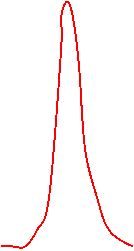
![]() Aria de sub curba lui f(t) este
egala cu unitatea, indiferent de forma curbei.
Aria de sub curba lui f(t) este
egala cu unitatea, indiferent de forma curbei.
f(t) f(t)
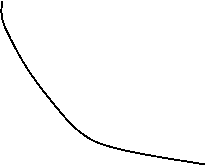
A =1 A = 1
![]()

t t
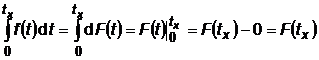
;
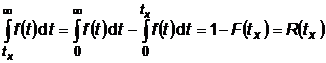
.
![]()
![]()
![]()
![]()
![]()
![]() f(t)
f(t)
f(t)
f(t)
![]()
![]()
 F(tx) R(tx)
F(tx) R(tx)
![]()
![]()

![]()
![]()
![]()
 F(tx) R(tx)
F(tx) R(tx)
![]()
![]()
tx t tx t
Densitatea de probabilitate a timpului de buna functionare:
permite aprecierea productiei daca se refera la dispozitive realizate de o singura firma (omogenitatea productiei);
ofera informatii privind omogenitatea solicitarilor in utilizare si a calitatii si frecventei operatiilor de mentenanta;
este utila in planificarea activitatii de mentenanta.
![]()
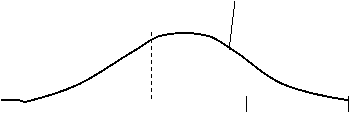
![]() f(t)
f(t)
A - inlocuire preventiva a dispozitivelor
B - inlocuirea disp. la aparitia defectelor
A
![]()
B
0
![]() t
t
tx tm tmaxA tmaxB
2.1.4 Rata de defectare (intensitatea momentana a caderilor), z(t)
RATA DE DEFECTARE reprezinta limita raportului
dintre probabilitatea ca un dispozitiv sa se defecteze in intervalul
deschis la stanga (t - Dt, t], deci cu conditia ca el sa
faca parte din dispozitivele care se aflau in buna stare de
functionare la inceputul
subintervalului, si marimea subintervalului Dt, cand aceasta tinde catre zero.
![]()
![]() .
.
Statistic reprezinta raportul dintre
numarul de defectiuni in unitatea de timp produse intr-un
subinterval de timp si numarul de dispozitive aflate in buna
stare de functiune la inceputul subintervalului de observare.
![]()
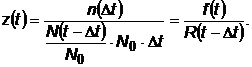
Daca t 0, atunci
![]()
T
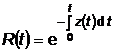
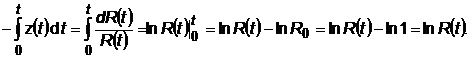
![]()
Rezulta: Daca z(t) = const. = atunci
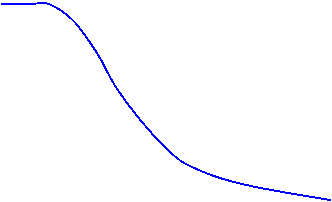
z(t)
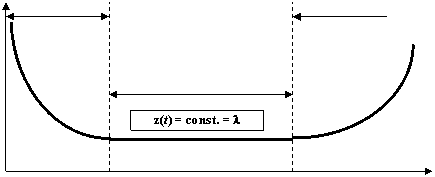 Rodaj Imbatranire
Rodaj Imbatranire
I II III
Viata utila
Timp
Rata de defectare:
permite compararea nivelului de fiabilitate al dispozitivelor realizate de diferiti producatori;
permite compararea conditiilor de utilizare a aceluiasi tip de dispozitive;
permite identificarea etapei din viata dispozitivelor si, implicit, a naturii defectiunilor;
Se exprima in defectiuni/unitatea de timp.
Probabilitatea ca un dispozitiv care s-a aflat in buna stare de functionare la momentul t1 sa se afle in aceeasi stare si la momentul t2 > t1
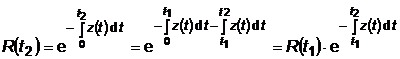
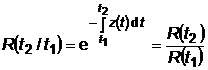
.
![]()
![]()
![]()
![]() R(t)
R(t)
![]()
![]() 1
1
![]()
![]() R(t1) R(t2/t1)
R(t1) R(t2/t1)
R(t)

![]() R(t2)
R(t2)
![]()
-t1 0 t1 t2 t
![]()
t2
Enunt Care este
probabilitatea de buna functionare a unei bobine de inductie
la momentul t2=44 000km, daca pana la t1=40
000 km ea s-a aflat in functiune? Pentru lotul de piese din care ea
face parte se cunoaste z(t)= l=5*10-5def./km. Rezolvare Se aplica
relatia de calcul pentru o probabilitate conditionata de
buna functionare: Pentru
intreaga populatie de bobine de inductie, la momentul t2
= 44 000km probabilitatea de buna functionare este:
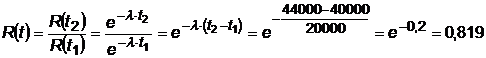
![]() <
R(t).
<
R(t).
APLICATIE NUMERICA

OBSERVATIE f(t) si z(t) fiind probabilitati de defectare in jurul unui
punct, ele se vor calcula, in
cazul observatiilor statistice, in raport cu mijlocul
fiecarui subinterval de observare
![]() .
.
2.1.5 Media timpului de buna functionare - MTBF
MTBF - in limba franceza: Moyenne des Temps de Bon Fonctionnement;
- in limba engleza: Mean Time Between Failures.
Prin definitie
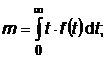 tI [0, +
tI [0, +
Cand se cunosc momentele producerii fiecarei defectiuni in parte,
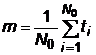
Cand observarea se face pe subintervale de timp,
![]()
![]()
![]()
n
n Dt

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() t*min t*max
t*min t*max
![]()
0 t0 t1 t2 ..ti-1 ti . tk-1 tk t
![]()
MTBF este un indicator sintetic care apreciaza nivelul global al fiabilitatii dispozitivelor.
2.1.6 Dispersia timpului de buna functionare, D
Prin definitie
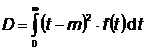
a) Se
cunoaste adevarata valoare a lui ![]() pentru intreaga populatie de dispozitive:
pentru intreaga populatie de dispozitive:
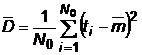
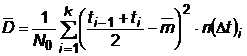
;
b) Nu se
cunoaste valoarea lui
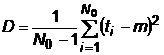
![]() pentru intreaga populatie de
dispozitive, ci doar valoarea lui m pentru esantionul studiat:
pentru intreaga populatie de
dispozitive, ci doar valoarea lui m pentru esantionul studiat:
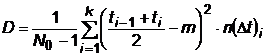
;
2.1.7 Abaterea medie patratica a timpului de buna functionare,
![]()
2.1.8 Eliminarea valorilor inregistrate eronat
Se calculeaza
marimea ![]() ,
,
Unde: tx este valoarea suspectata a fi eronata;
m - MTBF pentru esantionul studiat;
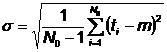 sau
sau 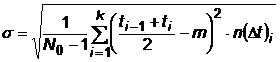 .
.
Din tabelul
functiei Laplace 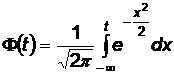 se determina z
se determina z
Se calculeaza marimea z
Daca N0 ∙ < 0,1 se elimina marimea suspecta tx cu o probabilitate de 99% ca ea sa fie eronata.
Enunt La incercarea unor dispozitive s-au inregistrat
urmatoarele momente de defectare, exprimate in ore de
functionare: 1121, 1123, 1124, 1125, 1125, 1126, 1126, 1127, 1128, 1135. sa se
verifice daca valoarea 1135 a fost inregistrata eronat. Rezolvare:
APLICATIE NUMERICA

2.2 Indicatori referitori la dispozitivele reparabile
Dispozitive reparabile - in cazul unei defectiuni sunt reparate, dupa care pot fi utilizate in continuare.
Ex.: motorul in ansamblul sau, schimbatorul de viteze etc.
![]() starea
starea
dipozitivului
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() buna funct.
buna funct.
tu1 tu2 . . . tun
![]()
![]()
![]()
![]()
![]()
![]() tr1 tr2 trn-1
tr1 tr2 trn-1
![]()
![]()
![]()
![]() defect
defect
t
Se definesc: 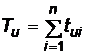 ,
timpul total de utilizare;
,
timpul total de utilizare;
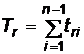 ,
timpul total de reparare.
,
timpul total de reparare.
2.2.1 Indicatori referitori la Tu
2.2.1.1 Functia de repartitie a Tu
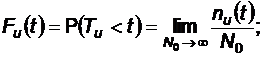
Pentru calcule statistice:
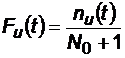
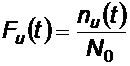
; daca N0 < 20 atunci: .
2.2.1.2 Densitatea de probabilitate a Tu
![]()
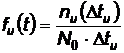
; .
2.2.1.3 Rata iesirii din utilizare
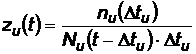
![]()
;
2.2.1.4 Media Tu
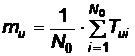
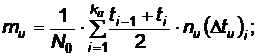
;
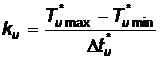
unde ku este numarul subintervalelor de observare: ,
unde T*umax, T*umin si t*u sunt valorile rotunjite la intreg ale marimilor respective.
2.2.1.5 Dispersia Tu
Cand se cunoaste valoarea mediei timpilor totali de utilizare pentru intreaga populatie de dispozitive:
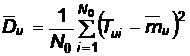
,
daca se inregistreaza momentele de iesire din functiune ale fiecarui dispozitiv in parte;
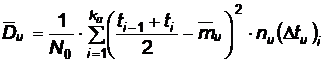
,
daca momentele de iesire din utilizare sunt inregistrate pe subintervale.
Cand nu se cunoaste valoarea mediei timpilor totali de utilizare pentru intreaga populatie de dispozitive, ci numai cea corespunzatoare esantionului studiat:
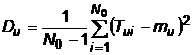
,
daca se inregistreaza momentele de iesire din functiune ale fiecarui dispozitiv in parte;
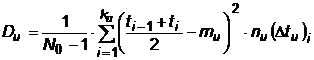
,
daca momentele de iesire din utilizare sunt inregistrate pe subintervale.
2.2.1.6 Abaterea medie patratica a Tu
![]()
2.2.2 Indicatori referitori la Tr
2.2.2.1 Functia de repartitie a Tr
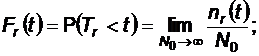
Pentru calcule statistice:
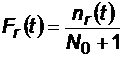
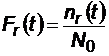
; daca N0 < 20, atunci: .
2.2.2.2 Densitatea de probabilitate a Tr
![]()
![]()
; .
2.2.2.3 Rata iesirii din reparatie
![]()
![]()
;
2.2.2.4 Media Tr
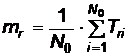
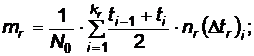
;
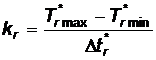
unde kr este numarul subintervalelor de observare: ,
unde T*r max, T*r min si t*r sunt valorile rotunjite la intreg ale marimilor respective.
2.2.2.5 Dispersia Tr
Cand se cunoaste valoarea mediei timpilor totali de reparare pentru intreaga populatie de dispozitive:
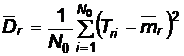
,
daca se inregistreaza momentele de iesire din reparatie ale fiecarui dispozitiv in parte;
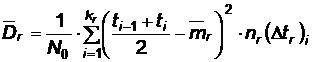
,
daca momentele de iesire din reparatie sunt inregistrate pe subintervale.
Cand nu se cunoaste valoarea mediei timpilor totali de reparare pentru intreaga populatie de dispozitive, ci numai cea corespunzatoare esantionului studiat:
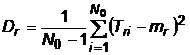
,
daca se inregistreaza momentele de iesire din reparatie ale fiecarui dispozitiv in parte;
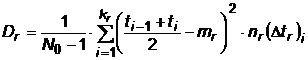
,
daca momentele de iesire din reparatie sunt inregistrate pe subintervale.
2.2.2.6 Abaterea medie patratica a Tr
![]()
2.2.3 Indicatori globali
2.2.3.1 Coeficientul de disponibilitate
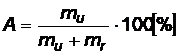
; A - Availability = disponibilitate (engl.)
2.2.3.2 Frecventa lucrarilor profilactice
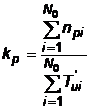
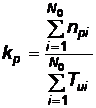
; unde npi este numarul lucrarilor profilactice efectuate asupra dispozitivului "i" ;
T'ui - timpul de utilizare a dispozitivului "i" in decursul experimentului.
2.2.3.3 Timpul specific pentru efectuarea lucrarilor profilactice
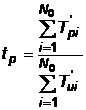
; unde T'pi este timpul consumat pentru lucrari profilactice la dispozitivul "i", in decursul experimentului.
2.2.3.4 Frecventa interventiilor corective
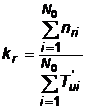
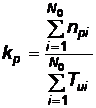
; unde nri este numarul interventiilor corective efectuate asupra dispozitivului "i", in decursul experimentului.
2.2.3.5 Timpul specific consumat pentru interventii corective
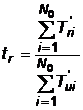
; unde T'ri este timpul consumat pentru interventii corective la dispozitivul "i", in decursul experimentului.