Utilizarea calculatorului de navigatie in aviatie

UTILIZAREA CALCULATORULUI DE NAVIGATIE IN AVIATIE

Utilizarea riglei de navigatie

In scopul reducerii timpului folosit pentru calculul elementelor de navigatie se folosesc riglele de calcul, in general de forme circula­re (exista si rigle de calcul drepte, de exemplu NL-10). Pentru aceasta se folosesc scari loga­ritmice, scale pentru conversiuni ale diferitelor unitati de masura, scale orare, roza vanturilor. Unele calculatoare dispun de caroiaje pentru lucrul cu date referitoare la vant. In aviatia civila se folosesc mai mult riglele de calcul circulare ARISTO AVIAT JEPPESEN si apltele.

Principalele operatiuni cu calculatoarele re­zulta din rezolvarea triunghiului de navigatie al vitezelor, care au la baza relatia fundamen­tala a trigonometriei plane, adica proportiona­litatea dintre laturile unui triunghi oarecare si sinusurile unghiurilor opuse, exprimata prin formule care utilizeaza calcul logaritmic.

Aplicand calculul prin logaritmi se obtine:

log VPA - log sin (1800-UVD) = log VS ­- log sin UVC = Vv - log sin . v .

Egalitatea diferentelor logaritmilor latu­rilor si unghiurilor opuse sta la baza contructiei calculatoarelor:

Log 1 fiind egal cu zero, originea masura­torilor pe cercul distantelor pe care se rapor­teaza laturile triunghiului de navigatie, al vi­tezelor, va fi 1 (respectiv 10 sau 100). De ase­menea, log sin 90° fiind egal cu zero, originea pe cercul gradelor pe care se raporteaza un­ghiurile triunghiului de navigatie al vitezelor va fi in dreptul gradatiei de 90.

O alta regula aplicabila calculatoarelor este aceea ca sinusu­rile a doua unghiuri suplimentare fiind egale si logaritmii lor vor fi egali. Datorita acestei reguli, unghiurile suplimentare se gasesc pe cercuI gradelor in dreptul acelorasi gradatii.

O regula specifica riglelor de calcul este aceea referitoare la citirea gradatiilor intrucat acest sistem permite multiplicarea lor cu 10, 100 etc, in raport de datele de baza ale pro­blemei. Astfel, cifra 15 se poate citi 150; 1500 ; 1,5 ; 0,15 etc.

Folosind tabelele de logaritmi, valorile de mai sus sunt rezolvabile prin :

- logaritmii valorilor naturale;

- logaritmii liniilor trigonometrice.

O atentie deosebita trebuie data diferitilor indici pe care fiecare calculator ii are marcati intr-un mod specific. In orioe caz, se vor gasi indici de unitate, de timp, de conversiuni ale unitatilor de masura etc.

De asemenea, diferitele scale ale calculatoarelor nu dau izolat rezolvarea integrala a unei probleme si rezultatele obtinute initial trebuie raportate la alte scale. Indicatii asupra folosirii tuturor scalelor de pe un calculator precum si exemple detailate se gasesc in instructiunile ce insotesc fiecare rigla de calcul. Insusirea in perfecte conditiuni a modului de folosire a ri­glelor asigura o corecta utilizare si implicit reducerea timpilor de calcul in rezolvarea pro­blemelor de navigatie aeriana.

Utilizarea riglei de navigatie se face pentru:

TAS, timpului si distantei

conversia unitatilor de masura

calculul combustibilului necesar

determinarea presiunii, densitatii si altitudinii adevarate

calcularea timpului de zbor pe ruta si ETA

Calculatorul de navigatie este destinat pentru navigatia automata, pe caile aeriene, in regiunile terminale si in zonele de aerodrom. El rezolva urmatoarele probleme:

a) calcularea continua a coordonatelor ac­tuale ale avionului prin metoda determinarii drumului real urmat ;

b) transformarea coordonatelor calculate;

c) zborul pe drumul distantei celei mai scurte, spre orice punet al traiectului;

d) corectarea coordonatelor calculate, dupa reperele radarului panoramic de blord ;            .

e) determinarea directiei si vitezei vantului;

f) producerea de semnale necesare pentru indicarea drumului pe indicatorul navigatoru­lui

g) producerea semnalelor necesare sistemu­lui pentru pilotarea automata a avio­nului.

Pentru rezolvarea tuturor problemelor de navigatie calculatorul foloseste sistemul coordonatelor ortodromice rectangulare si anume in doua moduri :

a) in regimul ortodromei principale cu axele de avionului ce coincide cu linia drumului obligat din pundul initial pana la punctul final al traiedului.

b) in regimul ortodromei partiale sau par­ticulare cu axele de coordonate

Folosirea acestui sistem de coordonate in calculator se bazeaza pe formule trigonome­trice relativ simple, care permit determinarea continua a locului avionului.

De asemenea, acest sistem permite intr-un mod simplu compararea coordonatelor pentru corectia locului avionului pe baza datelor mij­loacelor de radionavigatie, precum si efectua­rea manevrelor necesare acestor corectii, de­oarece coordonatele reprezinta intotdeauna abaterea laterala lineara de la linia drumului obligat iar S distanta ramasa pana la punctul obligator.

Compunerea generala a calculatorului de navigatie consta din urmatoarele elemente :

a) blocuri electronice si dispozitive electro­mecanice destinate pentru calculul, transfor­marea si corectia coordonatelor, calculul para­metrilor vantului, precum si a altor probleme;

b) panoul de comanda al regimurilor de lucru ;

c) panoul indicatorilor si inregistratoarelor care cuprinde: contoarele coordonatelor orto­dromice actuale ale avionului, contoarele coor­donatelor actuale transformate, inregistratoa­rele coordonatelor punctelor de schimbare a traiectului, inregistratoarele coordonatelor mij­loacelor de radionavigatie: destinate corectiei.

Deriva si corectiei de deriva

Unghiul de deriva

Ultimul element care determina modul de desfasurare a zborului este deriva sau unghiul de deriva, care se datoreaza directiei si vitezei de deplasare a masei de aer in care zboara aeronava. Prin deriva se intelege unghiul format intre prelungirea axei longitudinale a aeronavei si linia drumului real si se noteaza Dv.

Deriva aeronavei variaza in functie de viteza vantului, directia acestuia fata de LDO (Unghiul Drumului cu Vantul), cat si de viteza proprie a aeronavei (V.P.A.)

Variatia derivei se manifesta astfel:

cu cat viteza vantului este mai mare, cu atat unghiul derivei va fi mai mare;

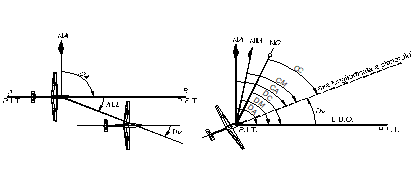
Fig. N.7.24. Deriva aeronavei

- cu cat unghiul directiei vantului fata de LDO (UDV) este mai mare, cu atat unghiul de deriva va fi mai mare. (UDV poate avea valori cuprinse intre 0^o si 180^o stanga/dreapta fata de LDO).

- cu cat viteza proprie a avionului este mai mare, cu atat unghiul de deriva este mai mic.