Probleme static nedeterminate la solicitarea axiala

Probleme static nedeterminate la solicitarea axiala

In unele probleme se intalnesc cazuri cand eforturile axiale nu pot fi determinate numai cu ajutorul ecuatiilor de echilibru cunoscute din statica. Problemele din acest grup sunt considerate static nederminate. Se ridica nedeterminarea din modul in care se produc deformatiile, folosind legatura dintre acestea si tensiunile care le-au produs se gasesc ecuatiile suplimentare necesare.

Se examineaza cele mai frecvente probleme static nedeterminate de intindere si compresiune intalnite in practica:

a). Bare cu sectiuni transversale neomogene.

Asamblarea din figura 84 este supusa la compresiune si dorim sa calculam tensiunile ce iau nastere in cele trei piese. Trebuie sa calculam repartitia fortei P in cele trei piese ( forta F₃ reprezentata pe un cerc, fortele F₁ si F₂ reprezentate pe doua coroane circulare) mentionam ca fortele F₁,F₂, F₃ sunt eforturi interioare din figura 85 . Facand o sectiune la o distanta (x) de capatul de sus, din echilibrul partii de sus rezulta, ecuatia vectoriala de echilibru care in mod implicit va duce la o ecuatie scalara.Vom obtine o singura ecuatie si exista trei necunoscute ( F₁, F₂, F₃ ) problema este dublu static nedeterminata, ridicam nedeterminarea din conditia de deformatii. ecuatia vectoriala iar ecuatia scalara va fi: F₁+F₂+F₃ - P = 0, F₁+F₂+F₃ = P ( 1 ) , o singura ecuatie si trei necunoscute , problema este dublu static nedeterminata . Din modul de asamblare trebuie ca scurtarile in cele trei piese sa fie egale. ∆l₁ = ∆l₂ = ∆l₃, ∆l₁=, ∆l₂= , ∆l₃ = , dar l₁=l₂=l₃=l, se va obtine ;F₂= ; F₃ = ; introducem in ecuatia ( 1 ) si obtinem F₁++ += P rezultaF₁= 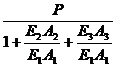apoi se

calculeaza F₂, F₃. Eforturile unitare normale din cele tre piese sunt:

=;=; = .

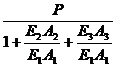
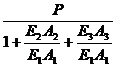
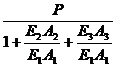
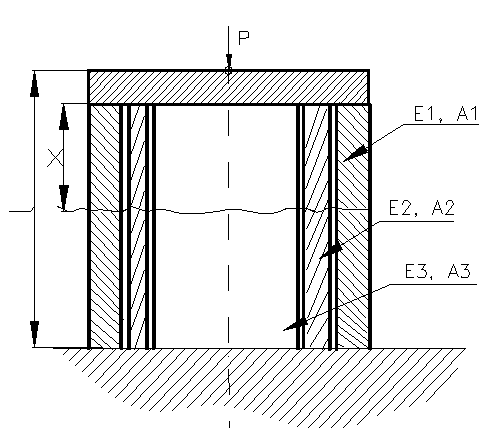
Figura 84

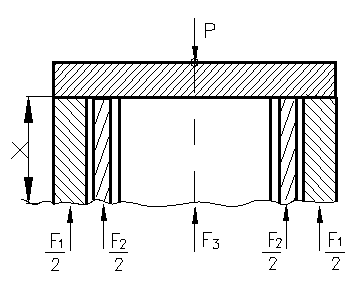
Figura 85

b) Bara articulata la ambele capete.

Din conditia de echilibru a barei va rezulta urmatoarele:

Ecuatia vectoriala de echilibru, , de unde , si de aici ecuatia scalara de echilibru, , o singura ecuatie si doua necunoscute ( H_A, H_B) problema este simplu static nedeterminata.

Deoarece reazemele A si B sunt fixe si se ia ca origine reazemul din A, deplasarea reazemului B fata de reazemul A este zero.

∆l_B= ∆l_I +∆l_II +∆l_III = 0 ; fiind aplicarea in mod indirect a primei teoreme a lui Castigliano, (1) ∆l_I = , ∆l_II = ,

∆l_III = ,

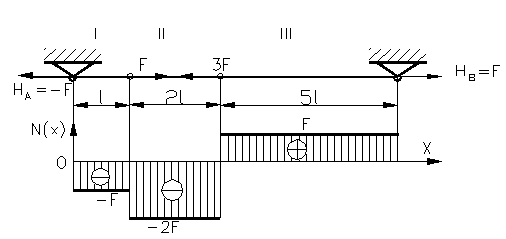
Figura 86

Regiunea intai x₁( 0; l ) ;N(x₁)=N_I = H_A.

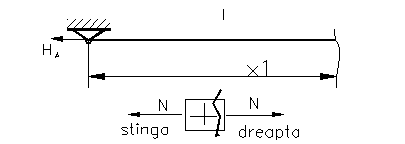
Figura 87

Regiunea a II-a x₂ ; N(x₂)=N_II=H_A-F.

Regiunea a III-a x₃

N(x₃)=N_III=H_A-F+3F, N(x₃)=H_A+2F, tinand cont si de relatia (1)0 =, E₁=E₂=E₃=E, A₁=A₂=A₃=A, se studiaza acest caz particular 0= H_A+2H_A-2F+5H_A+10F, 8H_A= -8F, H_A= -F folosind ecuatia scalara de

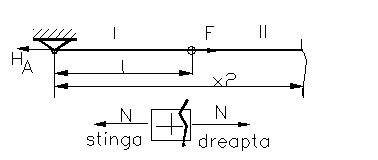
Figura 88

echilibru avem - F-H_B = - 2F; H_B= F ,

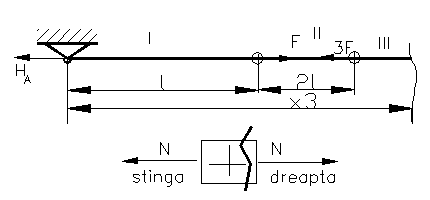
Figura 89

c) Sisteme static nedeterminate formate din bare articulate.

Se considera bara AF, articulata in A incarcata cu o forta in punctul F si legata prin patru tije verticale, de lungime l si rigiditati E_iA_i ca in figura 90. Sa se determine reactiunile din articulatie si eforturile interioare: din cele patru tije.

Folosim metoda sectiunilor, dupa ce se sectioneaza toate tijele, se indeparteaza tijele si in locul sectionat se pun eforturile interioare ca in figura 90. Se ia bara orizontala separat si se scriu conditiile de echilibru din figura 91, , de unde rezulta ecuatiile scalare de echilibru:, din rezulta H_A= 0

; V_A+N₁+N₂+N₃+N₄-P = 0 (1)

;

N₁l₁+N₂ (l₁+l₂) +N₃( l₁+l₂+l₃ ) + N₄ (l₁+l₂+l₃ +l₄ ) - P (l₁+l₂+l₃ +l₄ +l₅ ) = 0 (2).

Sunt doua ecuatii si cinci necunoscute ( N₁, N₂, N₃, N₄, V_A ) problema este triplu static nedeterminata.

Ridicam nedeterminarea din conditia de deformatie a barei , se pune restrictia ca bara orizontala AF sa aiba o rigiditate mare , deci ramane rectilinie atunci cand sistemul se deformeaza. ∆h₁=, ∆h₂= ; ∆h₃= ; ∆h₄= ,(3) iar din figura 90 reiese ca

h₁= h₂= h₃= h₄= h ;

S-au format mai multe triunghiuri asemenea ,aplicand teorema lui Thales din figura 92, ; ; tinand cont de relatiile (3) vom avea ; , (4)

N₂=; N₃= ; N₄=;(5)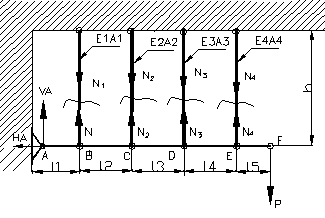             

Figura 90

Din relatiile (5) si (2) se afla eforturile: N₁, N₂, N₃, N₄ pentru ca s-a obtinut un sistem de cinci ecuatii cu cinci necunoscute , compatibil unic determinat ∆₅, admite o solutie unica.

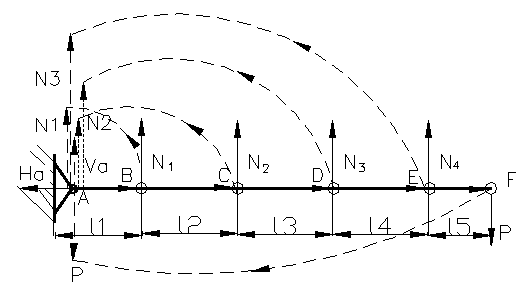
Figura 91

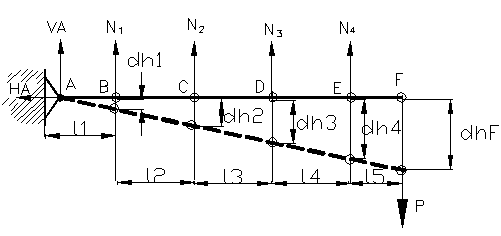
Figura 92

d) Bare incastrate la ambele capete solicitate axial.

Din figura 93 exista forte active numai pe orizontala,ca urmare vom avea forte de reactiune numai pe orizontala, acest lucru este valabil numai pentru barele drepte. Se pun conditiile de echilibru;; H_A+2F-5F+F-H_B = 0 ; H_A- H_B= 2F; (1) .Bara este simplu static nedeterminata , ridicam nedeterminarea din conditia de deformatie a barei. Incastrarea din A este fixa, la fel si

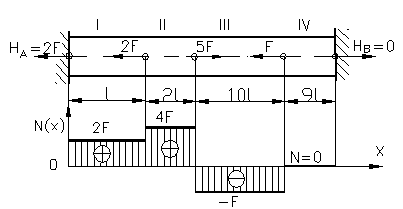
Figura 93

incastrarea din B, daca luam ca origine capatul din incastrarea A, atunci deplasarea punctului B fata de A este zero.

∆l_tB = ∆l_I+∆l_II+∆l_III+∆l_IV = =0 E₁A₁=E₂A₂=E₃A₃=E₄A₄=EA;

Regiunea intai, x₁( 0,l ) N(x₁)= H_A

Regiunea a II-a; x₂ N(x₂)= H_A+2F.

Regiunea a III-a; x₃

N(x₃)=H_A+2F- 5F;N(x₃)= H_A- 3F

Regiunea a IV-a; x_{4 ;}

N(x₄)=H_A+2F- 5F+F = H_A- 2F ∆l_tB=0=; H_A+2H_A+4F+10H_A- 30 F +9H_A- 18F= 0 ; 0=22H_A- 44F; H_A=2F, folosind (1) rezulta H_B=0, se inlocuisc valorile fortelor de reactiune si se traseaza diagrama de eforturi.

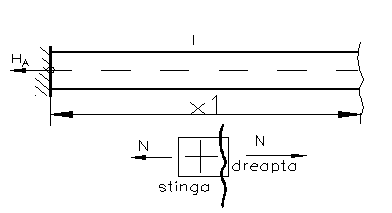
Figura 94

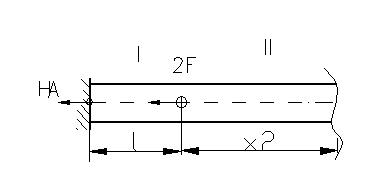
Figura 95

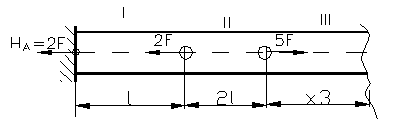
Figura 96

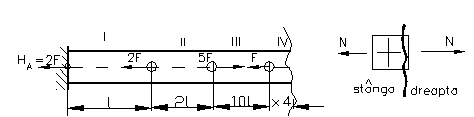
Figura 97

∆l_tB=0=; H_A+2H_A+4F+10H_A- 30 F +9H_A- 18F= 0 ; 0=22H_A- 44F; H_A=2F, folosind (1) rezulta H_B=0, se inlocuisc valorile fortelor de reactiune si se traseaza diagrama de eforturi.

Regiunea intai; x₁( 0,l ); N(x₁)= H_A=2F

Regiunea a II-a; x₂N(x₂)= H_A+2F=2F+2F=4F

Regiunea a III-a; x₃N(x₃)=H_A+2F- 5F;

N(x₃)= H_A- 3F=2F-3F= -F

Regiunea a IV-a; x₄N(x₄)=H_A+2F- 5F+F;

N(x₄)=H_A- 2F=2F-2F=0

Metoda a II-a .

Aplicam prima teorema lui Castigliano. Din , reiese ca

H_A-H_B= 2F ; o singura ecuatie si doua necunoscute,se alege ca necunoscuta static nedeterminata H_A . Explicitam cealalta necunoscuta H_B functie de necunoscuta static nedeterminata H_A,anume H_B=H_A-2F.

Regiunea intai x_1,N(x₁)=H_A,

Regiunea a II-a x_2, N(x₂)=H_A+2F,

Regiunea a III-a x_3, N(x₃)=H_A+2F-5F=H_A-3F;

Regiunea a IV-a x₄ N(x₄)=H_A+2F-5F+F=H_A-2F, ;W=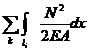 energia potentiala de deformatie , iar

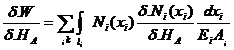0=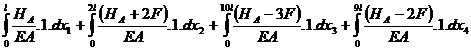

0= = ∆l_I + ∆l_II + ∆l_III + +∆l_IV; de aceea se scrie direct ∆l_i fara a mai folosi prima teorema a lui Castigliano. Acest procedeu se aplica numai barelor drepte .

e). Sisteme de bare concurente.

Consideram cazul barelor concurente din figura 98, asupra carora in punctul Q actioneazaforta concentrata P , se cere sa se calculeze tensiunile din cele trei bare din materiale si sectiuni diferite.

Se scriu ecutiile de echilibru: , N₁sin-N₃sin=0; (1)

, N₁cos+N₂+N₃cos-P=0 (2) sunt doua ecuatii: (1), (2) dar avem trei necunoscute (N₁,N₂,N₃), problema este simplu static nedeterminata. Ridicam nedeterminarea cu ajutorul primei teoreme a lui Castigliano. Alegem ca necunoscuta static nedeterminata pe N₃ si explicitam celelalte doua necunoscute N₁,N₂ functie de N₃. Din ecuatiile (1), (2) se obtine:N₁=N₃(3)   respectiv

N₂= P- N₃(ctgsin+cos) (4)l₁ = NQ; l₂ = MQ ; l₃ = QS Aplicam teorema lui Castigliano: 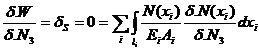punctul (S) este fix. Bara intii x₁(0;l₁) N(x₁)=N₁= N₃si

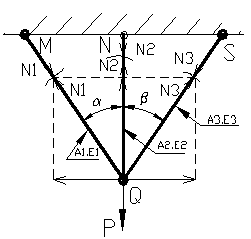
Figura 98

Bara a II-a x₂(0;l₂) N(x₂)=N₂= P-N₃(ctgsin+cos)

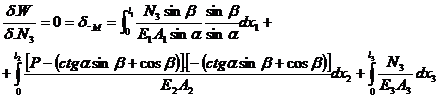
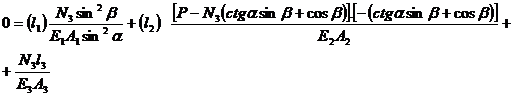
l₂=l₁cosα = l₃cosβ N₃=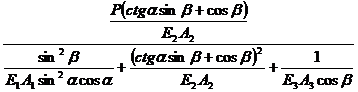, din relatiile (3) si

(4) rezulta N_1,respectiv N₂ , ,.

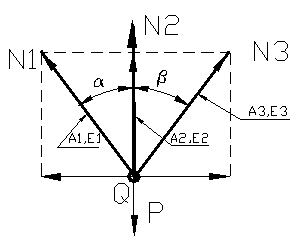
Figura 99