Proprietati termoelectrice ale conductoarelor

PROPRIETATI TERMOELECTRICE ALE CONDUCTOARELOR

Fenomenele ce au loc la punerea in contact a semiconductorilor se regasesc, in parte pe aceleasi baze fizice, si in cazul metalelor si aliajelor de naturi diferite, avand drept consecinta aparitia unei diferente de potential intre corpurile respective.

Elementele metalice au fost aranjate ( de catre Volta) intr‑o succesiune, numita seria lui Volta: Al, Zn, Sn, Cd, Pb, Sb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd, astfel ca la pu­nerea in contact a doua (sau mai multora) dintre ele, cel ce se afla mai in fata obtine potentialul mai electropozitiv. Aparitia diferentei de potential intre piesele metalice aflate in contact, la o temperatura data (T) este determinata de energiile de extractie a electronilor, diferite de la un metal la altul si de diferenta intre concentratiile de electroni liberi. Diferenta de potential varaiza cu temperatura.

Daca se considera doua metale (sau aliaje) diferite (A) si (B) inainte de pune­rea lor in contact, zonele de conducti si respectiv nivelele Fermi diferite, se vor situat pe scara energiilor ca in fig. 3.8, in care s‑a notat cu (j_A= respectiv (j_B) energia de extractie a electronului din atomul metalului respectiv. S‑a considerat ca (j_B < j_A

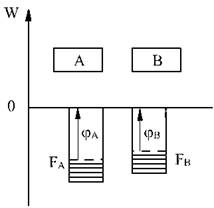
Figura 3.8. Nivelele energetice ale metalelor inaintea punerii in contact

Dupa punerea in contact a celor doua metale admitand ca modificarilor ener­gi­ei si potentialului sunt reprezentate numai de catre metalul (B), cum (j_B < j_A), va avea loc difuzia de electroni dinspre (B) spre (A). Difuzia se continua pana cand se stinge echilibrul termodinamic, cand nivelele Fermi (F_A) si (F_B) coincid. Diferentei energiilor de extractie, care apare ii corespunde o diferenta de potential, astfel ca se poate scrie:

(3.16)

unde s‑a notat cu . In fig. 3.9. este reprezentata diagrama nivelelor de energie corespunzatoare metalelor (A) si (B) dupa punerea lor in contact.

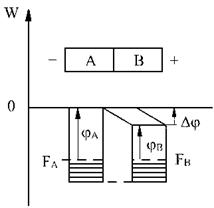
Figura 3.9. Nivele energetice ale metalelor in contact

Daca se considera si concentratiile de electroni (n_A) si (n_B) ale celor doua me­tale ca fiind diferite, de exemplu n_B > n_A, rezulta ca aceasta constituie o noua cauza a difuziei de electroni din (A) spre (B) ceea ce determina aparitia a inca unei diferente de potential (U'_AB). In ipotezele admise pentru energiile de extractie si pentru con­cen­tratiile de electroni rezulta ca metalul (B) pierde electroni, ramanand cu un exces de sarcina pozitiva (deci ca potential pozitiv), iar metalul (B) primind electroni va obtine un potential negativ. Campul electric de difuzie care apare stabileste echilibrul intre campul de difuzie si concentratiile electronilor se poate stabili mai operativ ape­land la teoria clasica, deci asimiland electroni liberi cu gazul perfect.

Din teoria cineticp a gazelor se deduce ca pentru un gaz cu "n" molecule pe unitatea de volum, avand fiecare energia medie (W), presiunea pe care gazul o exer­cita asupra unitatii de suprafata (de exemplu considerand incinta ca fiind un cub cu aria fortei egala cu unitatea), tinand seama de cele trei grade de libertate ale mole­cu­lei, ca fiind:

(3.17)

sau cum energia medie a moleculei, la temperatura (T), este:

(3.18)

rezulta ca (3.17) devine:

(3.19)

Daca se considera un tub elementar de lungime (dx) si sectiunea (sD) plasat in zona de frontiera dintre metalul (A) si metalul (B) astfel ca baza (a) a acestuia sa se afle in (A) iar baza (b) in (B), rezulta ca daca in (a) concentratia este (n) iar presiunea (p), in (b) concentratia va fi (n+dn) iar presiunea (p+dp), incat pe baza relatiei (4.36) rezulta:

(3.20)

sau:

(3.21)

Forta care deplaseaza surplusul de molecule (respectiv electroni) din (b) spre (a) este de natura mecanica si rezulta din:

(3.22)

Pe de alta parte aparitia, in urma difuziei, a diferentei de potential si a cam­pu­lui electric de difuzie (F = -dV/dx), asupra electronilor va actiona forta de natura elec­trica

(3.23)

Cum cele doua forte (4.39) si (4.40) la echilibru sunt egale si opuse, rezulta ca:

(3.24)

Integrand (4.41) intre (V'_A) si (V'_B) respectiv (n_A) si (n_B) se obtin diferenta de potential:

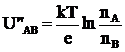(3.25)

Diferenta de potential rezultanta, tinand seama de (3.16) si (3.25) este:

(3.26)

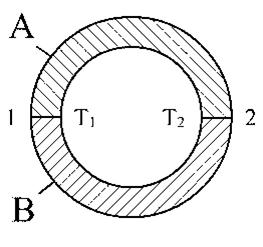
Figura 3.10. Principiul termocuplului

Datorita faptului ca (U'_AB) este functie de temperatura (T) a suprafetei de con­tact dintr metale, rezulta ca se poate constitui o masura a temperaturii. Deci contactul intre doua metale sau aliaje diferite poate constitui un traductor pentru masurarea tem­peraturii pe cale electrica.

Tensiunea (U_AB) dependenta de temperatura se mai numeste si tensiune termo­electromotoare de contact (prescurtat: t.t.e.m.c.).

Traductorul de temperatura a carui functionare are la baza relatia (3.26) se nu­meste traductor termoelectric sau termocuplu si poate fi utilizat pentru masurari de temperaturi de la (10-15) °K pana la cateva mii de grade.

In principiu utilizarea relatiei (3.26) pentru etalonarea termocuplului deriva din considerarea acestuia pentru cazul unui circuit inchis, format de cele doua metale (A) si (B), ca in fig. 3.10. Se considera ca temperatura (T₁) este mai mare decat (T₂). In punctul cald (1), cum i se spune suprafetei de contact (1), tensiunea termoelec­tromo­toare de contact este:

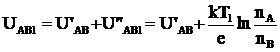(3.27)

iar in punctul rece (2) este:

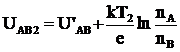(3.28)

La ambele suprafete de contact (U'_AB) fiind aceeasi rezulta ca (t.t.e.m.c.) ca su­ma geometrica intre (U_AB1) si (U_AB2) este:

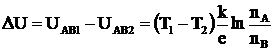(3.29)

in care:

k - este constanta lui Boltzmann;

e - este sarcina electronului.

Notand factorii parantezei cu o constanta (A₀) rezulta ca (3.29) devine:

(3.30)

sau daca se realizeaza (T₂ = 0) rezulta ca DU masoara numai temperatura punctului cald (1) si:

(3.31)

Termocupla se obtine in principiu, prin deschiderea circuitului din fig. 3.10 in punctul (2) si conectarea capetelor libere la un milivoltmetru, care dupa etalonare este gradat direct in unitati de temperatura. Reprezentarea conventionala a termocuplului se face in fig. 3.11. La utilizarea in practica a termocuplului se mentine constanta tem­peratura (T₂) sau chiar nula, incat tensiunea masurata sa fie functie numai de tem­peratura punctului cald (1) introdus in incinta a carei temperatura se masoara.

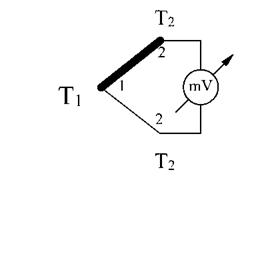
Figura 3.11. Masura temperaturii cu termocuplul

Tinand seama de (3.30) este necesar ca pentru termocuple sa se utilizeze meto­de si aliaje care sa asigure liniaritatea acestei dependente si sa determine o sensi­bi­litate cat mai mare. Ca metale se utilizeaza: Fe, Cu, Ag, Ni, Ir, W, Cr, Pt etc. De asemenea se utilizeaza aliaje, in special in practica se remarca: 1. Constantanul (40% Ni + 60% Cu), 2. Copelul (44% Ni + 2% Mn+Cu); 3. Alumelul (95% Ni+Al, Si, Mg); 4. Cromelul (90% Ni + 10% Cr), sau aliajul pe baza de platina rhodiata (90% Pt + 10% Rh). Perechile de aliaje alese in practica depind de valoarea temperaturii ce urmeaza a fi masurate. Ca exemple se considera: 1) Fe - Constantan; 2) Ag - Copel; 3) Cromel - Copel, toate pentru 600 [°C]; 4) Cromel - Alumel 1000 [°C]; 5) PtRh - Pt 1600 [°C]; W-WM₀ 1800 °C si 7) I_r - I_rR_t 2300 °C. Pentru temperaturi criogene se foloseste Cu - Constantan pana la (-257 [°C] sau elemente din aliaje nobile pana la (-255 °C) avand insa o sensibilizare mai mare decat primele. De obicei primul ele­ment al perechii este cel care obtine potentialul mai electropozitiv si este reprezentat in fig. 3.11 cu linie mai groasa.