Determinarea acceleratiei caderii libere cu ajutorul pendulului matematic

DETERMINAREA ACCELERATIEI CADERII LIBERE CU AJUTORUL PENDULULUI MATEMATIC

Aparate si accesorii: pendulul matematic,cronometru,scala milimetrica.

Notiuni teoretice:

Toate corpurile materiale sunt supuse atractiei reciproce cu forta determinata de legea atractiei universale: F=G·m₁m₂/r² (1) , unde m₁ si m₂ -masele corpurilor ce interactioneaza , r-distanta dintre ele;G-constanta gravitationala,numeric egala cu forta cu care interactioneaza doua corpuri cu masele unitare ce se afla la o distanta de o unitate (in SI:masele a cite 1kg la distanta dintre ele de 1m).

Forta de interactiune dintre corpul cu masa m ce se gaseste pe suprafata Pamintului si Pamint cu masa M se scrie in felul urmator: F=G·mM/R² (2), unde R-raza Pamintului.La suprafata

Pamintului intre forta de atractie F si masa corpului m exista relatia F=mg, (3),unde g-acceleratia caderii libere ce poate fi exprimata,avand in vedere (2),prin relatia g=G·M/R² (4).

Mentionam ca egalitatea dintre forta de atractie si forta de greutate P=mg are loc numai la poli.In celelalte puncte ale Pamintului,datorita rotatiei in jurul axiei proprii,este necesar de tinut cont si de forta centrifuga de inertie: f_in=mω²r ,unde ω-viteza unghiulara de rotatie a Pamintului,r-distanta corpului considerat pina la axa de rotatie a Pamintului.

La poli (r =0,f_in=0) forta de atractie F coincide cu forta de greutate P si acceleratiei caderii libere,are valoarea maxima.La ecuator "r'are valoare maxima si,prin urmare,f_in tot este maxima,iar P este minima si g atinge valoarea minima.

Diferenta dintre fortele de greutate P si atractiei F este mica deoarece forta centrifuga de inertie f_in este cu mult mai mica decat forta de atractie.

Este necesar de tinut cont si de faptul ca Pamintul nu are forma strict sferica,raza lui la poli fiind mai mica decit la ecuator.Deaceea valoarea maxima g la poli este 9,832 m/s²,iar la ecuator este minima egala cu 9,780m/s².La latitudinea noastra g=9,81m/s².

Pentru determinarea acceleratiei caderii libere se poate folosi metoda pendulului matematic,baza careia sta dependenta perioadei oscilatiei pendulului matematic de acceleratia caderii libere g si lungimea pendulului "l".

Se numeste perioada T a oscilatiei a pendulului matematic timpul in care pendulul efectueaza o oscilatie completa,deplasindu-se intr-o parte si apoi in cealalta parte de la pozitia de echilibru.

Descrierea instalatiei,teoria metodei:

Se numeste pendul matematic sistemul idealizat care consta dintr-un corp (considerat punct material)cu masa "m"suspendat printr-un fir imponderabil si inextensibil de lungime "l".O aproximatie destul de buna a pendulului matematic serveste o bila de diametru mic,confectionata dintr-un metal de densitate mare (1),suspendata cu ajutorul unui fir lung si subtire(2).

Firul este trecut pe un scripete(3),iar capatul al doilea al firului este fixat pe placa(4),pozitia careia poate fi modificata,schimbind lungimea pendulului.Modificarea lungimei pendulului este determinta cu ajutorul scalei milimetrice.In pozitia de echilibru forta de greutate care actioneaza asupra bilei P=mg este echilibrata de forta de tensiune a firului,astfel pendulul ramine in repaus.Daca scoatem pendulul din pozitia de echilibru,de exemplu,il abatem in punctul "c"(vezi fig.1) la un oarecare unghi α,atunci forta de greutate poate fi descompusa in doua componente:F₁=mg sinα si F₂=mg cosα (5).Forta F₂ este orientata d-ea lungul firului si e numita componenta normala,forta F₁ este perpendiculara pe un fir si e numita componenta tangentiala.

In oarecare alta pozitie decit cea de echilibru,forta de tensiune din fir este echilibrata de componenta normala F₂ a fortei de greutate.Componenta tangentiala F₁ tinde sa readuca sistemul spre pozitia de echilibru si este numita forta de restabilire.

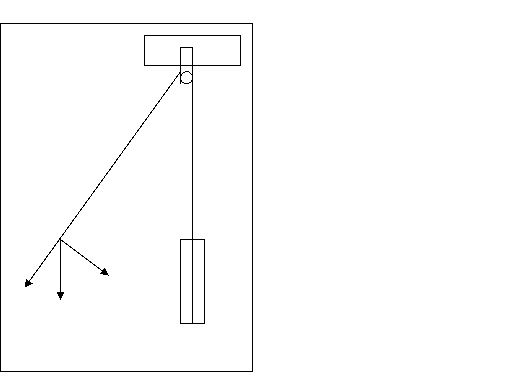
Figura1.

Din figura se vede ca sinα=F₁/mg.Miscarea oscilatorie a centrului de masa a bilei din punctul C in punctul simetric C¹,situate de cealalta parte a punctului de echilibru al sistemului,este o miscare de rotatie in jurul punctului de suspensie a firului,iar unghiulα este elongatia unghiulara.Momentul cinetic al punctului material de masa "m" este L=lω (6),unde I=ml² este momentul de inertie,iar ω=dα/dt este viteza unghiulara al acestuia.

Conform teoremei variatiei momentului cinetic dL/dt =M (7), unde M=-mgl sinα este momentul de rotatie a bilei pendulului de masa "m",putem scrie d/dt(L·ω)=-mgl.sinα (8).

Inlocuind in relatia (8) L si ω se obtine ecuatia d²α/dt²+g/l·sinα=0 (9).

Asa cum forta de restabilire nu este proportionala cu elongatia ω (adica nu are forma F₁=-kx),miscarea pendulului matematic (gravitational)nu este intotdeauna o miscare oscilatorie armonica.Daca insa unghiul α fiind exprimat in radiani,este mic(α<5-6⁰) sinα ≈α si F₁ ≈m g α.Arcul cuprins intre pozitia verticala a firului si pozitia dupa abaterea pendulului poate fi considerat elongatie a bilei x,astfel ca α=x/l (10), "l" fiind lungimea firului.

Din figura se vede F₁ este orientata in sens contrar elongatiei si,deci,F₁=-mg·x/l (11), adica este de forma F=-kx,unde k este raportul k=m·g/l (12).

Adica forta de restabilire a echilibrului este o forta cvazi elastica,fiind proportionala cu distanta x de la pozitia de echilibru si orientata permanent spre pozitia de echilibru.Pe de alta parte aceasta forta de tip elastic imprima pendulului accelaratie,determinate de principiul al doilea al mecanicii m a=-kx,din care se obtine,tinind cont ca a=d²x/dt², m·d²x/dt²+kx=0 (13).

Aceasta este ecuatia cu care se descrie oscilatia armonica a pendulului in raport cu pozitia de echilibru (x=0),pulsatia careia este ω=√k/m=√g/l (14).

Perioada de oscilatie a pendulului se determina dupa relatia T=2π/ω si tinind cont de relatia (14),putem scrie T=2π·√l/g

(15).Relatia (14) este confirmata de datele experimentale.

Din relatia (15) rezulta ca una din legile pendulului gravitational,care afirma ca perioada nu depinde de elongatia unghiulara(pentru α≤5⁰-6⁰) cunoscuta sub numele de legea izovronismului micilor oscilatii.Din ea rezulta determinarea acceleratiei caderii libere "g" se reduce la determinarea lungimei "l" si perioade "T" de oscilatie a pendulului matematic.

Determinarea valorii exacte a lungimii pendulului matematic este dificila,de aceea se procedeaza in felul urmator.Se determina perioadele de oscilatie a pendulului cu lungimi diferite,pentru care putem scrie:T₁=2π√l₁/gsi T₂=2π√l₂/g ,unde rezulta ca g=4π²(l₂-l₁)/T₁ ²-T₂² (16).

Prin urmare,pentru determinarea acceleratiei caderii libere este suficient sa fie determinate perioadele de oscilatii ale pendulului si diferenta de lungimi ∆1=l₂-l₁-marime,care se determina cu ajutorul scalei milimetrice.

Modul de lucru:

Se fixeaza pozitia placii 4(fig.1) in una din pozitiile indicate de catre cadrul didactic (l!).

Cu ajutorul cronometrului se determina timpul a 50 oscilatii complete.experienta se repeta nu mai putin de 3-5 ori.

Se fixeaza placa 4 in a doua pozitie (l!!) si se repeta masuratorile dupa cum a fost descrise mai sus.

Se determina diferenta pozitiilor l!!-l!=l₂-l₁ reprezinta diferenta lungimilor a doua pendule cu masele egale si lungimi diferite.

Datele experimentale vor fi introduse in tabelul 1.

FORMULELE DE CALCUL:

∆l=│l_med-l₁│

∆T=0.05

g=4π²l/T²

∆g=│g-g₁│

E=∆g/g₁·100

1 Vor fi calculate perioadele de oscilatie T₁=t₁/n si T₂=t₂/n, unde t₁,t₂ sunt intervale de timp necesare pentru efectuarea numarului "n" de oscilatii complete ale pendulului.

2 Se va calcula acceleratia "g" folosind valorile medii pentru T₁ si T₂.

3 Vor fi calculate erorile absolute si relative ale determinarii lui "g".

4 Va fi verificata legea izocronismului oscilatiilor mici efectuind determinarea si compararea perioadelor de oscilatii T functiiei elongatia α pentru valori mici ale lui α.