Legatura spatiu-timp in descrierea unei traiectorii

Legatura spatiu-timp in descrierea unei traiectorii

Fie un exemplu de traiectorie liniara intr-un plan cartezian (fig.4.9) :

Fig.nr.4.9. O dreapta oarecare in plan

Ecuatia dreptei estey = m· x+ n (4.2.)

unde:

- m este panta dreptei

- n este taietura dreptei.

Prin derivare:

(4.3)

Procedand la impartire cu dt atat la numitor cat si la numarator :

(4.4)

Presupunand ca aceasta dreapta trebuie descrisa intr-un plan de punctul caracteristic, iar acesta se misca cu viteza constanta dupa directia axei coordonatei x si tot cu viteza constanta dupa directia axei coordonatei y, iar raportul celor doua viteze este m, punctul caracteristic va descrie in plan o dreapta de panta m.

Continuand rationamentul: 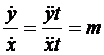(4.5)

Daca cele doua miscari dupa directia axelor de coordonate sunt uniform accelerate, iar raportul acceleratiilor este m, atunci in plan se descrie o dreapta de panta m.

Adica daca pe fiecare dintre axele Ox si Oy se alege cate o lege de miscare:

(4.6)

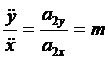si (4.7)

atunci in plan este descrisa o dreapta.

Observatie : in exemplul considerat s-a constatat ca urmarind o anumita evolutie in timp se obtine o anumita forma a traiectoriei din spatiul cartezian.

Din punct de vedere practic, realizarea unei drepte in plan se obtine alegand portiuni cu miscare uniform accelerata si portiuni cu miscare rectilinie uniforma.

Fie o dreapta in plan ce se presupune a deveni o traiectorie impusa (fig.4.10.)

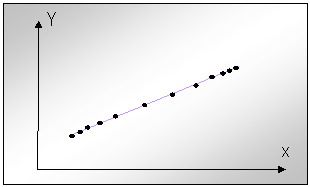
Fig.nr.4.10 Puncte alese pe o traiectorie liniara

Pe aceasta dreapta se aleg mai multe puncte tinta si via. In mod intentionat la inceputul si sfarsitul parcurgerii dreptei se aleg puncte amplasate mai des, iar pe mijlocul liniei se aleg puncte amplasate mai rar. Pentru descrierea acestei drepte, in miscare, este necesar ca la inceputul si sfarsitul trasarii ei miscarea dupa x si y sa se efectueze uniform accelerat cu:

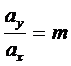(4.8)

unde m este panta dreptei.

pe portiunea din mijloc se impune ca miscarea sa se efectueze cu viteze constante:

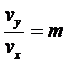(4.9)

iar la sfarsitul dreptei miscarile se fac uniform incetinit cu :

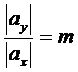.(4.10)

Deci daca se conduce robotul dupa un profil trapezoidal de viteza, dupa fiecare dintre axele x si y, atunci in plan punctul caracteristic descrie o dreapta cu panta :

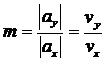(4.11)

Observatii :

1). Pe portiunile de accelerare si decelerare punctele de pe dreapta nu sunt echidistante in spatiu, dar sunt echidistante in timp. Adica spatiul parcurs intre un punct si altul ( pe portiunile de accelerare) este diferit, dar intervalul de timp intre ele este acelasi.

2). Pe fiecare dintre coordonatele x si y se alege cate o lege de miscare cu profil trapezoidal de viteza, cu:

,

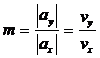iar in spatiu se traseaza o dreapta de panta m.

3). Situatia se poate generaliza si in spatiul tridimensional pentru trasarea unei drepte in spatiu.

4). O astfel de metoda de conducere este direct aplicabila in cazul unui robot T.T.T.

5). Legile de miscare rectilinie uniform accelerata:

(4.6)

si rectilinie uniforma:

(4.12)

sunt functii line ( functia si primele sale doua derivate sunt continue), deci miscarea per ansamblu este lina.

6). In cazul unui robot diferit de configuratia T.T.T. metoda se aplica mai greu deoarece :

o deplasare cu constante nu inseamna implicit si o deplasare cu v=ct. si a =ct. la nivelul fiecarui motor amplasat la cate o cupla cinematica conducatoare. In general vitezele si acceleratiile pe x si y si cele de la nivelul fiecarei cuple cinematice conducatoare se stabilesc cu Jacobianul.

panta m a dreptei este impusa de traiectoria dorita si nu intotdeauna se pot sintetiza si practic viteze de valori astfel incat raportul lor sa fie chiar m. De cele mai multe ori se admite deplasarea cu viteze aflate intr-un raport cat mai apropiat de m si se accepta o anumita abatere de la dreapta impusa.

De multe ori, impunand anumite valori ale vitezei pe axele x si z si efectuand calculul cu Jacobianul pot rezulta viteze, la nivelul cuplelor cinematice conducatoare, nerealizabile fizic. In aceasta situatie se alege, la nivelul fiecarei cuple cinematice conducatoare, cea mai apropiata valoare realizabila fizic pentru viteza si se sintetizeaza deplasari cu aceste viteze rezultand o traiectorie numai aproximativ exacta.

Concluzii : metoda descrisa este direct aplicabila pentru o structura de mecanism T.T.T., este deosebit de utila pentru intelegerea legaturii spatiu-timp in conducerea unui robot, dar se aplica mai greu in cazul altor tipuri de roboti.