
|
|
|
Tensiuni cauzate de variatii de temperatura
Fie o bara de lungime ( l ) executata dintr-un material cu coeficient de dilatare termica liniara ( α) , sufera o crestere de temperatura uniforma ∆t=t1-t0 ea se alungeste cu cantitatea ∆lt = αl∆t= αl (t1-t0). In sisteme static nedeterminate dilatarile sunt in parte sau total impiedicate, ceea ce duce la producerea unor eforturi unitare in bare. Se considera cazul barei din figura 101, incastrata la ambele capete, care nu permit nici o dilatare , incastrarile se opun lungirii, fapt ce duce la aparitia unei forte de compresiune cu efect opus dilatarii . Acest lucru se exprima analitic prin conditia , deformatia totala a barei este nula .
∆ltotal
=αl∆t- ![]() =0, de aici rezulta ca N =EAα∆t, iar efortul unitar
cauzat de dilatarea impiedicata este: σ = Eα∆t = E
α (t1-t0). Cazul in care la un capat al barei
va fi un joc cunoscut δ ( rost de dilatatie ) din figura 100, relatia
de deformatie se scrie: αl∆t
-
=0, de aici rezulta ca N =EAα∆t, iar efortul unitar
cauzat de dilatarea impiedicata este: σ = Eα∆t = E
α (t1-t0). Cazul in care la un capat al barei
va fi un joc cunoscut δ ( rost de dilatatie ) din figura 100, relatia
de deformatie se scrie: αl∆t
- ![]() =δ de unde
rezulta N. Daca N rezulta negativ, insemna ca
dilatarea nu umple rostul si deci nu se produc eforturi unitare termice.
=δ de unde
rezulta N. Daca N rezulta negativ, insemna ca
dilatarea nu umple rostul si deci nu se produc eforturi unitare termice.
Vom studia urmatoarea problema din figura 101 bara fiind formata din patru tronsoane, de sectiuni, lungimi si materiale diferite, incastrata la ambele capete si supusa unei variatii de temperatura t0 ( s C ) . Deoarece deformatia datorita variatiei de temperatura este impiedicata, in cele doua reazeme iau nastere reactiuni egale cu H. Daca se elimina reazemul din B atunci bara se va lungi termic cu: ∆lt= (α1l1+α2l2+α3l3+α4l4) t0, unde α1, α2, α3, α4 sunt coeficienti de dilatare termica liniara a fiecarui tronson in parte .
Reactiunea H produce o scurtare mecanica iar deformatia mecanica este egala cu dilatarea termica.
∆lm = ![]() = H (
= H (![]() )
)
∆ltotal = ∆ltermic-∆lmecanic=0; ∆ltermic=∆lmecanic
sau dupa notatia de mai sus ∆lt=∆lm ;(α1l1+α2l2+α3l3+α4l4)
t0 = H (![]() )
)
H = 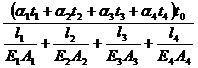 , iar tensiunile normale
, iar tensiunile normale ![]() ;
; ![]() ;
;![]() .
.
Deplasarea sectiunii transvesale corespunzatoare punctului D rezulta din diferenta dintre deformatia termica si cea mecanica:
∆lD= ∆l1t-∆l1m+∆l2t-∆l2m=
α1l1t0 - ![]() +α2l2t0 -
+α2l2t0 - ![]()
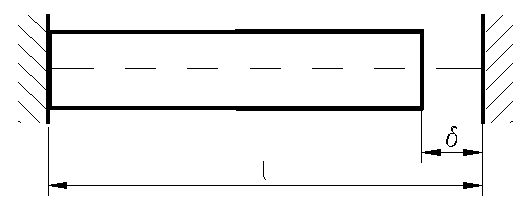
Figura 100
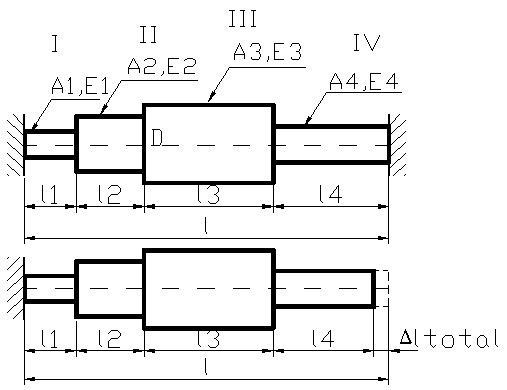
Figura 101
Problema nr.4
Sa se
dimensioneze bara din figura 102 si sa se calculeze deplasarea
liniara a sectiunii din punctul C, stiind ca bara este
executata dintr-un material avand σa=105![]() iar E=2,1.105
iar E=2,1.105![]() ;q0=2
;q0=2![]() ; l1=q0 [m]; l2=0,2m; l3 = 0,3m ; l4 = 0,7m , incarcarea
distribuita dupa legea : x(y) =
q(y) =
; l1=q0 [m]; l2=0,2m; l3 = 0,3m ; l4 = 0,7m , incarcarea
distribuita dupa legea : x(y) =
q(y) = ![]() arcsiny .
arcsiny .
Rezolvare:
Trebuie sa se tina cont de functiile inverse si respectiv functiile directe , de unde deriva toate legaturile .
Se neglijeaza momentele incovoietoare care iau nastere.
Avand incarcarea axiala distribuita dupa legea:
x(y) = q(y) = ![]() arcsiny ; cu
originea in O, rezultanta fortelor distribuite axiale va fi:
arcsiny ; cu
originea in O, rezultanta fortelor distribuite axiale va fi:
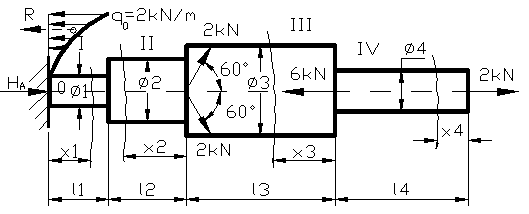
Figura 102
R=Rez=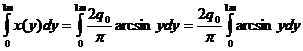 ;
; 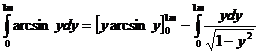 (1) in relatia aceasta s-a folosit metoda
integrarii prin parti, unde f(y)=arcsiny; f' (y)=
(1) in relatia aceasta s-a folosit metoda
integrarii prin parti, unde f(y)=arcsiny; f' (y)=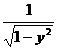 dg=dy
dg=dy
![]() g(y)=y;
g(y)=y; 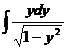 se face
schimbarea de variabila
se face
schimbarea de variabila
1-y2=t2,d(1-y2)=d(t2), -2ydy=2tdt, de undeydy= -tdt 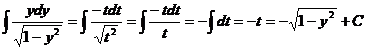
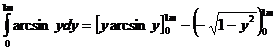 =1arcsin1-1=
=1arcsin1-1=![]() - 1 revenind la
calculul rezultantei R=2
- 1 revenind la
calculul rezultantei R=2![]() =0,726 kN=aria triunghiului curbiliniu AMN=AAMN
=0,726 kN=aria triunghiului curbiliniu AMN=AAMN
Nota:![]()
![]() proprietatile
functiilor inversabile, din desen s-a dat functia pentru y(x) = sin
proprietatile
functiilor inversabile, din desen s-a dat functia pentru y(x) = sin![]() ; arcsiny(x) = arcsin
sin
; arcsiny(x) = arcsin
sin![]() de unde reiese
ca
de unde reiese
ca ![]() = arcsiny(x), x(y) = 2
= arcsiny(x), x(y) = 2![]() arcsiny aceasta este
functia incarcarii pentru regiunea intai a barei , mentionam
ca daca
arcsiny aceasta este
functia incarcarii pentru regiunea intai a barei , mentionam
ca daca
( y) va fi mare atunci solicitarea produsa de fortele axiale distribuite o sa fie o solicitare compusa , care va fi abordata la un alt capitol.
Se poate calcula rezultanta R in mai multe moduri care se fac pe parcurs.
Aria triunghiului curbiliniu AQM, va fi : AAQM=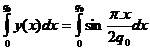 se face schimbarea de variabila
se face schimbarea de variabila ![]() = u, d(
= u, d(![]() ) = du,
) = du,
(![]() )'dx= du,
)'dx= du, ![]() dx = du; dx = 2
dx = du; dx = 2![]() du;
du;
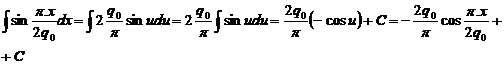
AAQM= 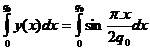 = -
= - 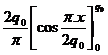 =2
=2![]() , aria totala a
, aria totala a
dreptunghiului AQMNeste eg![]() ala cu
ala cu ![]() =AAQMN de unde calculam AAMN=AAQMN-AAQM=
=AAQMN de unde calculam AAMN=AAQMN-AAQM=![]() se prezinta mai multe posibilitati de calcul.
flam forta de reactiune HA din incastrare din
conditia de echilibru,
se prezinta mai multe posibilitati de calcul.
flam forta de reactiune HA din incastrare din
conditia de echilibru, ![]()
-HA+R-2kN+6kN-2kN=0;-HA+0,726+2kN=0, HA=2,726 kN,se imparte bara in regiuni sau zone.
Regiunea intai
x1![]() (0;l1) si y1
(0;l1) si y1![]() (0;1m) N(y)= -HA+R(y);R(y)=
(0;1m) N(y)= -HA+R(y);R(y)=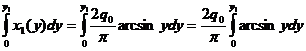 =
=![]() +
+
+![]() R(y)=
R(y)=![]() ,
, ![]() - 2,726=N(y), se face
graficul functiei N(y) in mod normal
- 2,726=N(y), se face
graficul functiei N(y) in mod normal ![]() - 2,726 kN;
- 2,726 kN;![]() N(y)= - 2,726 +0,726= -2kN, N'(y)=
N(y)= - 2,726 +0,726= -2kN, N'(y)=![]() arcsiny > 0; N"(y)=
arcsiny > 0; N"(y)=
![]()
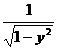 > 0. Se mai poate reprezenta grafic functia N(y)
si astfel:
> 0. Se mai poate reprezenta grafic functia N(y)
si astfel:
q(y) = x(y)= ![]() arcsiny; y(x) = sin
arcsiny; y(x) = sin![]() ; arcsiny =
; arcsiny = ![]() ; N(y) se expliciteaza
functie de x si se va obtine expresia urmatoare pentru
efortul interior N din prima regiune.
; N(y) se expliciteaza
functie de x si se va obtine expresia urmatoare pentru
efortul interior N din prima regiune.
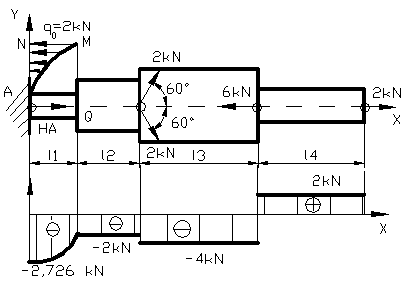
Figura 103
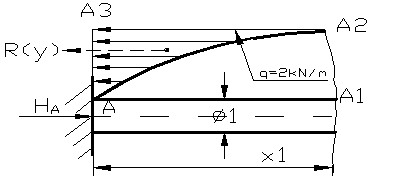
Figura 104
Cand se afla cele doua expresii, se rezolva cea mai simpla dintre ele.
N(x)=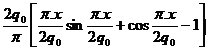 -2,726kN .
-2,726kN .
Metoda a II-a de calcul a expresiei R(y) si in mod implicit a lui N(y)
Aria dreptunghiului AA1A2A3=xy=ADREPT; din figura 104
aria AA1A2=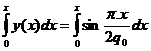
Aria AA1A2= - 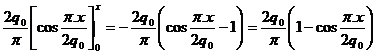 ,
,
aria AA2A3=ariaAA!A2A3-aria
AA1A2=xy-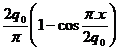 ; stiind
; stiind
ca x(y)=2![]() arcsiny si
arcsiny si
cos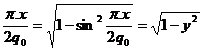 ; aria AA2A3=
; aria AA2A3=![]() =R(y) s-a obtinut aceiasi expresie.
=R(y) s-a obtinut aceiasi expresie.
Metoda a III-a de calcul a expresiei lui N(y)
Metoda integrarii este o metoda universal valabila , care se foloseste cel mai frecvent , aceasta metoda derivand din relatiile diferentiale dintre sarcini si eforturi . In toate problemele din rezistenta materialelor vor rezulta ecuatii diferentiale cu variabile separabile, unde solutiile lor sunt integrale si totodata trebuie sa tinem cont si de conditiile initiale ale lui Cauchy . Se sectioneaza bara la o distanta oarecare (x) se da o crestere elementara lui (x) anume (dx), se impune conditia de echilibru pentru tronsonul din bara dx , la capetele tronsonului de bara se inlocuiesc actiunea fortelor exterioare cu eforturile interioare ce au luat nastere conform principiului actiunii si reactiunii.
Din conditia de echilibru va rezulta (figura 105):
![]() , deciN(y)+dR(y)-
, deciN(y)+dR(y)-![]() ;N(y)+dR(y)-N(y)- dN(y)=0;
;N(y)+dR(y)-N(y)- dN(y)=0;
dN(y)=dR(y) integram aceasta relatie de
unde rezulta, ![]() ;
;
N(y)=![]() =
= ![]() ; de unde va rezulta aceiasi expresie pentru calculul
N(y).
; de unde va rezulta aceiasi expresie pentru calculul
N(y).
Regiunea
a II-ax2![]() ( 0; 0,2m )
( 0; 0,2m )
N(x2)=2kN-6kN+2kNcos60s=2kN-6kN+2kN; N(x2)= - 2kN
Regiunea
a III-ax3 ![]() ( 0; 0,3m ) N(x3)=2kN- 6kN= - 4kN
( 0; 0,3m ) N(x3)=2kN- 6kN= - 4kN
Regiunea
a IV-ax4![]() ( 0; 0,7m )
( 0; 0,7m )
N(x4)=2kN
Deoarece bara este executata din tronsoane de diametre diferite se se face dimensionarea pentru fiecare tronson in parte . In sectiunea in care avem forta axiala exterioara concentrata , trebuie ca in diagrama de forte axiale sa avem un salt.
Valoarea absoluta a saltului trebuie sa fie egala cu valoarea absoluta a fortei axiale concentrate exterioare din acea sectiune.
Relatia de dimensionare va fi: Anec=![]()
![]() d=
d=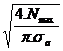
d1=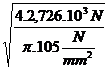 =5,74mm
=5,74mm![]() 6mm,d2=
6mm,d2=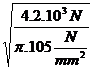 =4,92
=4,92![]() 5mm; d3=
5mm; d3=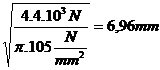
![]() 7mm; d4=
7mm; d4=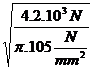 =4,9
=4,9![]() 5mm;
5mm;
Pentru calculul deplasarii liniare a punctului (C)
folosim prima teorema a lui Castigliano, dar trebuie ca forta 2kN din
punctul (C) sa o notam cu Pc si tocmai la
sfarsitul problemei sa inlocuim Pc=2kN, deoarece avem
derivatele partiale ![]() .
.
In mod implicit se recalculeaza forta
de reactiune HA functie de Pc, deci se face din
nou:![]() HA- 0,726kN+2kN-6kN+Pc=0 HA=4,726-Pc . Deplasarea liniara a sectiunii
transversale din punctul C va fi: dlc=
HA- 0,726kN+2kN-6kN+Pc=0 HA=4,726-Pc . Deplasarea liniara a sectiunii
transversale din punctul C va fi: dlc=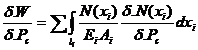
Figura 105
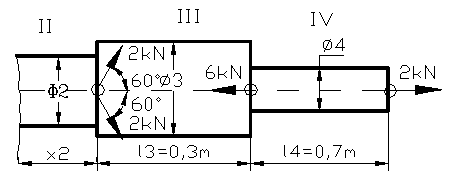
Figura 106
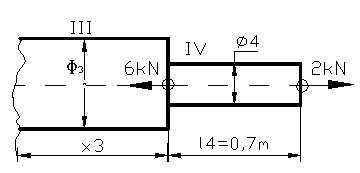
Figura 107
In cazul teoremelor lui Castigliano este indicat sa se foloseasca si tabele pentru a fi mai usor de urmarit rezolvarea problemelor .
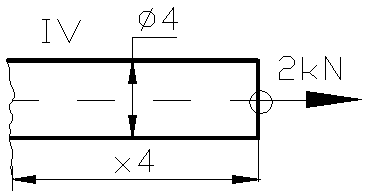
Figura 108
dlc=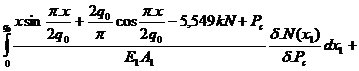
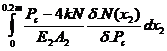 +
+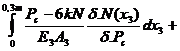
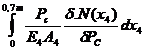
dlc=dl1+dl2+dl3+dl4 = -4,146 mm; E1=E2=E3=E4=E(modulele de elasticitate longitudinale ); dlc = - 4,146 mm.
Regiunea
N(xi)
![]()
xi![]() ( )
( )
intai
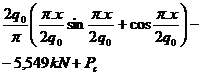
1
x1![]() (0;
(0;![]()
a II-a
Pc-4kN
1
x2![]()
( 0;0,2m )
a III-a
Pc-6kN
1
x3![]()
(0; 0,3m )
a IV-a
Pc
1
x4![]()
( 0; 0,7m )
Problema nr.5
Sa se verifice bara verticala de otel de lungime l=4m si este executata dintr-un material avand σa=106 N/mm2 , supusa la o forta de intindere P=2kN la capatul liber si sa se calculeze deplasarea liniara a capatului C . Stiind ca: E=2,1.105 N/mm2; γg=7,8 Kgf/dm3, bara din figura 110.
Rezolvare:
Deoarece bara este incastrata la un capat si libera la celalalt capat se poate trasa direct diagrama de eforturi interioare , dar trebuie sa luam ca origine capatul liber al barei si aceasta origine sa ramana neschimbata pe tot timpul rezolvarii problemei . Nu mai trebuie sa calculam forta de reactiune din (A) pentru ca va reiesi direct din diagrama de eforturi .
Regiunea intai x1![]() ( 0;
( 0; ![]() ] sau x1
] sau x1![]() ( 0; 1,33 dm ]
( 0; 1,33 dm ]
q1=γg.A1
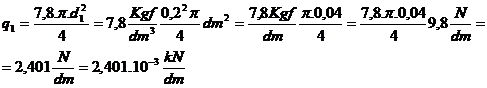
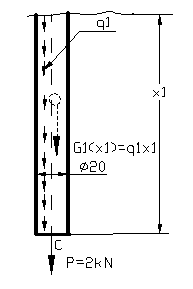
Figura 109
N(x1)=P+q1x1=2kN+2,401.10-3kN/dm.x1 este o dreapta in planul
X O N(x) ![]() N(x1)=2kN;
N(x1)=2kN;![]() N(x1)=2kN+2,401.
N(x1)=2kN+2,401.![]() .1,33dm=
.1,33dm=
2kN+3,193.10-3kN=2,003193kN.
Regiunea a II-a
x2![]() (0;1,33dm] ; N(x2)
= P+ G1+ q2x2= 2kN + γgA1l1+
q2x2;G1=7,8
(0;1,33dm] ; N(x2)
= P+ G1+ q2x2= 2kN + γgA1l1+
q2x2;G1=7,8![]()
![]() =q1.l1=2,401
=q1.l1=2,401![]() .1,33dm=0,003193kN
.1,33dm=0,003193kN
N(x2)=2,003193kN+q2x2
dar q2=γgA2=![]() ; N(x2)=2,003193kN+9,605.
; N(x2)=2,003193kN+9,605.![]() x2;
x2; ![]() N(x2)=2,003193 kN ;
N(x2)=2,003193 kN ;![]() N(x2)=2,003193kN+9,605. 10-3.1,33kN=2,015kNG2=q2۰l2=9,605
N(x2)=2,003193kN+9,605. 10-3.1,33kN=2,015kNG2=q2۰l2=9,605![]() ۰1,33 dm=12,77465 N=12,77465۰10-3 kN
۰1,33 dm=12,77465 N=12,77465۰10-3 kN
Regiunea a III-a x3![]() ( 0; 0,66 dm ]
( 0; 0,66 dm ]
N(x3)= P + G1+G2+
q3۰x3 G1= 0,003193 kN G2=0,012774 kNN(x3)
=2kN + 0,003193 kN+0,012774 kN+21,612![]() ۰x3=2,015967 kN +21,612
۰x3=2,015967 kN +21,612![]() ۰x3,
q3=γg۰A3=7,8
۰x3,
q3=γg۰A3=7,8![]() ۰
۰![]() =2,205398
=2,205398![]() =2,205398۰9,8
=2,205398۰9,8![]() =21,612 N/dm = 21,612 .10-3 kN/dm ; N(x3)= 2,015967 kN +21,612
=21,612 N/dm = 21,612 .10-3 kN/dm ; N(x3)= 2,015967 kN +21,612![]() ۰x3;
۰x3; ![]() N(x3)=2,015967 kN
N(x3)=2,015967 kN ![]() N(x3)=2,0302kN
N(x3)=2,0302kN
G3=q3۰l3=
21,612![]() ۰0,66 dm=14,26392 N=0,01426 kN
۰0,66 dm=14,26392 N=0,01426 kN
Regiunea a IV-a
x4![]() (0; 0,66 dm ] q4=γg۰A4=7,8
(0; 0,66 dm ] q4=γg۰A4=7,8![]() ۰
۰![]() =1,5315
=1,5315![]() =1,5315۰9,8
=1,5315۰9,8![]() =15,008
=15,008![]() .
.
G4=q4۰l4=15,008![]() ۰0,66 dm=9,90528 N=0,009905 kN
۰0,66 dm=9,90528 N=0,009905 kN
N(x4) = P + G1+
G2 + G3 + q4۰x4 = 2 kN
+0,003193 kN+0,012774 kN +0,01426 kN+15,008![]() ۰x4
۰x4
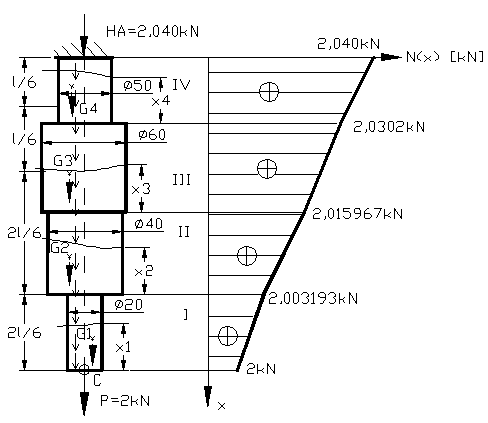 Figura 110
Figura 110
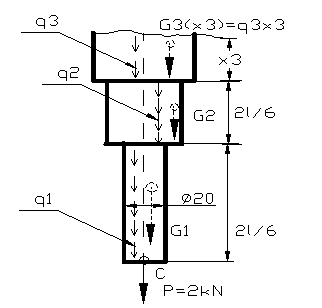
Figura 112
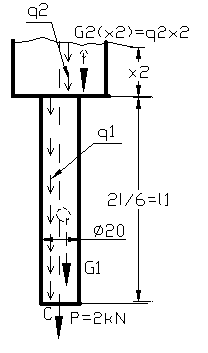
Figura 111
N(x4)=2,0302 kN+
15,008![]() ۰x4 ;
۰x4 ; ![]() N(x4)=2,0302
kN ;
N(x4)=2,0302
kN ;
![]() N(x4)=2,040
kN
N(x4)=2,040
kN
Bara fiind executata din tronsoane de diametre diferite se face verificarea pentru fiecare tronson in parte.
Sectiunea periculoasa este sectiunea in care forta axiala este maxima in valoare absoluta.
![]() =
=![]() aceasta este relatia
de verificare
aceasta este relatia
de verificare
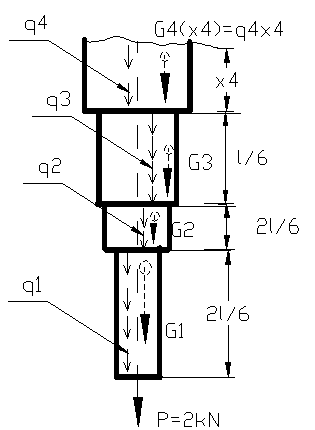
Figura 113
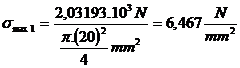
![]() ;
;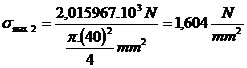
![]() ;
; 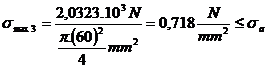 ;
;![]()
![]()
dlc=dl1+dl2+dl3+dl4=
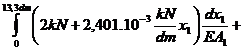
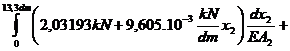
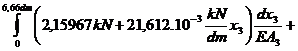
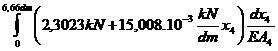 = 0,0086195 dm .
= 0,0086195 dm .