
|
|
|
. REZULTATE FUNDAMENTALE IN DUALITATEA IN PROGRAMAREA LINIARA
Definitia 1. Se numeste problema duala a problemei de programare liniara (1):
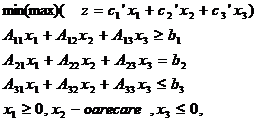 (1)
(1)
unde:
![]()
![]()
![]()
![]()
![]()
![]()
problema de programare liniara (2):
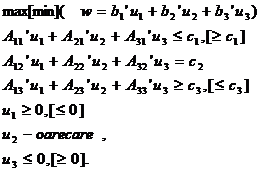 (2)
(2)
Modelele (1) respectiv (2), in detaliu, devin modelele (1') respectiv (2'), asadar, problema duala a problemei de programare liniara (1'):
![]()
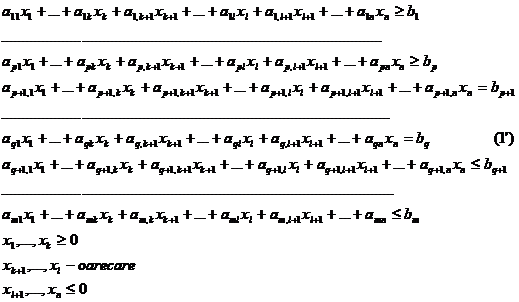
este problema de programare liniara (2'):
![]()
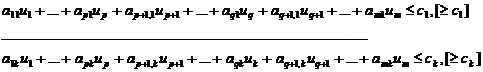
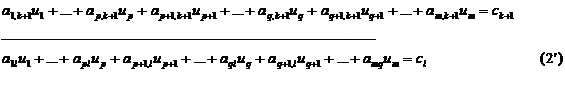
![]()
![]()
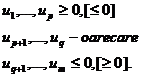
Observatie. Problema duala a unei probleme de programare liniara se obtine, pornind de la problema primala, cu respectarea urmatoarele reguli:
(i). Oricarei
restrictii a problemei primale ii corespunde o variabila in problema
duala (numita variabila duala); unei restrictii
exprimate printr-o inegalitate ii corespunde o variabila duala cu
restrictii de semn, iar unei restrictii exprimate printr-o egalitate ii
corespunde o variabila duala fara restrictii de semn;
mai exact unei restrictii exprimate printr-o inegalitate de tipul "![]() " ii corespunde o variabila duala nenegativa,
iar unei restrictii exprimate printr-o inegalitate de tipul "
" ii corespunde o variabila duala nenegativa,
iar unei restrictii exprimate printr-o inegalitate de tipul "![]() " ii corespunde o variabila duala nepozitiva, in
cazul unei probleme primale de minimizat, semnele variabilelor duale inversandu-se
in cazul in care problema primala este de maximizat.
" ii corespunde o variabila duala nepozitiva, in
cazul unei probleme primale de minimizat, semnele variabilelor duale inversandu-se
in cazul in care problema primala este de maximizat.
(ii). Oricarei
variabile a problemei primale ii corespunde o restrictie in problema duala;
unei variabile cu restrictii de semn ii va corespunde o restrictie
exprimata printr-o inegalitate, iar unei variabile fara restrictii
de semn ii corespunde o restrictie exprimata printr-o egalitate; mai
exact unei variabile nenegative ii corespunde o inegalitate de tipul "![]() ", in timp ce unei variabile nepozitive ii corespunde o
inegalitate de tipul "
", in timp ce unei variabile nepozitive ii corespunde o
inegalitate de tipul "![]() " daca problema primala este o problema de
minimizat, tipul restrictiilor duale inversandu-se in cazul in care
problema primala este de maximizat.
" daca problema primala este o problema de
minimizat, tipul restrictiilor duale inversandu-se in cazul in care
problema primala este de maximizat.
(iii). Coeficientii variabilei duale de indice "i" sunt elementele liniei "i" din problema primala, asadar matricea coeficientilor restrictiilor problemei duale este matricea transpusa a matricei coeficientilor restrictiilor problemei primale.
(iv). Daca functia obiectiv a problemei primale se minimizeaza (maximizeaza) atunci functia obiectiv a problemei duale se maximizeaza (minimizeaza); coeficientii functiei obiectiv a problemei duale sunt termenii liberi ai restrictiilor problemei primale si termenii liberi ai restrictiilor problemei duale sunt coeficientii functiei obiectiv a problemei primale.
Observatii: (i). Problema duala a unei probleme de programare liniara sub forma generala este tot o problema de programare liniara sub forma generala.
(ii). Problema duala a unei probleme de programare liniara sub forma standard nu este o problema sub forma standard; problema duala problemei (3):
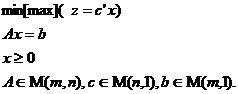 (3)
(3)
este problema (4).
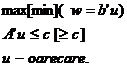 (4)
(4)
(iii). Duala unei probleme de programare liniara sub forma canonica este tot o problema de programare liniara sub forma canonica, motiv pentru care consideratiile de dualitate in programarea liniara se fac indeosebi asupra problemelor sub forma canonica; problemele duale ale problemelor (5), respectiv (6) sunt problemele (7), respectiv (8):
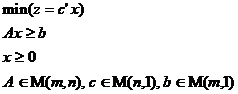 (5)
(5)
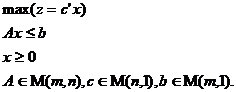
![]() (6)
(6)
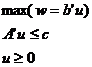 (7)
(7)
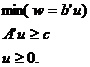 (8)
(8)
(iv). Dualitatea in programarea liniara are caracter involutiv, adica problema duala a unei problemei duale a unei probleme de programare liniara este problema initiala (primala); din aceasta cauza vom spune ca doua probleme de programare liniara duale una alteia formeaza un cuplu de probleme de programare liniara duale. Spre exemplu, problemele duale ale problemelor (7), respectiv (8) sunt problemele (5), respectiv (6):
(v). Problemele duale a doua probleme de programare liniara echivalente (probleme care se obtin una din alta prin transformari elementare) sunt probleme echivalente.
In contextul dualitatii ne propunem sa prezentam cinci rezultate reprezentative. Pentru primele patru teoreme vom considera cuplul de probleme de programare liniara sub forma canonica (5), (7), iar pentru ultimul rezultat preferam sa consideram cuplul format din problema de programare liniara sub forma standard (3) si duala sa (4), pentru ca pentru problema standard vom formula algoritmul simplex-dual.
Teorema 1. (Teorema fundamentala a dualitatii). Pentru orice cuplu de probleme de programare liniara duale este posibila una si numai una dintre urmatoarele trei afirmatii:
(i). ambele probleme admit programe; in acest caz ambele probleme admit programe optime, pentru care functiile obiectiv coincid;
(ii). una dintre probleme admite programe iar cealalta nu; in acest caz problema care admite programe are optim infinit;
(iii). nici una dintre probleme nu admite programe.
Pentru demonstrarea teoremei, vom prezenta in prealabil trei leme ajutatoare.
Consideram asadar cuplul de probleme duale (5), (7).
Notam: P = - multimea programelor problemei (5);
D = - multimea programelor problemei (7).
Lema 1. Pentru orice pereche de programe duale ![]() P,
P, ![]() D este adevarata
inegalitatea: b'
D este adevarata
inegalitatea: b'![]() ≤c'
≤c'![]() .
.
Intr-adevar,
![]() P
P![]()
![]() ;
;
![]() ;
;
rezulta de aici ca
![]() .
.
Lema 2. Daca ![]() si
si ![]() atunci
atunci ![]() este program optim pentru
problema (5), iar
este program optim pentru
problema (5), iar ![]() este program optim pentru problema (7).
este program optim pentru problema (7).
Aplicam
lema 1 perechii de programe ![]() , u
, u![]() , u - oarecare;
rezulta:
, u - oarecare;
rezulta:
b'u≤![]() =
=![]() ,
,![]() D,
D,
adica ![]() este program optim pentru problema (7).
este program optim pentru problema (7).
Procedand analog cu perechea de programe x![]() P, x -
oarecare,
P, x -
oarecare, ![]() D rezulta:
D rezulta:
![]() =
=![]() ≤c'x,
≤c'x, ![]() P,
P,
deci ![]() este program optim pentru problema (5).
este program optim pentru problema (5).
Lema 3. Daca dintr-un cuplu de probleme de programare duale una are optim infinit, atunci cealalta problema nu are programe; daca una dintre probleme are program optim , cealalta problema nu poate avea optim infinit.
Pentru demonstratie este suficient sa remarcam faptul ca:
![]() .
.
Demonstratia teoremei
Asociem cuplului de probleme de programare liniara duale (5), (7) matricea antisimetrica
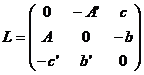 ;
;
facem apel la urmatoarea
consecinta a teoremei Farkas-Minkowski [ ]: pentru orice matrice
antisimetrica L![]() Mn(R) exista un vector
Mn(R) exista un vector ![]()
![]() Rn astfel incat sa avem:
Rn astfel incat sa avem:
![]() ;
;
in cazul nostru exista ![]()
![]() Rn+m+1 astfel incat:
Rn+m+1 astfel incat:
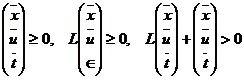 , (9)
, (9)
adica in detaliu:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
Deoarece ![]() exista doua posibilitati:
exista doua posibilitati:
(i). ![]() . Din (10)-(11) rezulta ca:
. Din (10)-(11) rezulta ca:
![]()
iar din (13)-(14) rezulta ca:
![]() si
si ![]() ,
,
asadar ![]() P,
P, ![]() . Din (15) si lema
1 rezulta ca
. Din (15) si lema
1 rezulta ca ![]() , iar in baza lemei 2
, iar in baza lemei 2
![]() si
si ![]() sunt programe optime pentru problemele (5), respectiv (7).
sunt programe optime pentru problemele (5), respectiv (7).
(ii). ![]() . Demonstram, in acest caz, ca nu este posibil ca ambele
probleme duale (5) si (7) sa admita programe. Intr-adevar,
daca presupunem ca problema (5) admite programul x si problema (7) admite programul u, atunci:
. Demonstram, in acest caz, ca nu este posibil ca ambele
probleme duale (5) si (7) sa admita programe. Intr-adevar,
daca presupunem ca problema (5) admite programul x si problema (7) admite programul u, atunci:
Ax ≥ b, x ≥ 0;
A'u ≤ c, u ≥ 0.
In aceste condttii rezulta urmatoarele inegalitati contradictorii:
![]() ;
;
![]() ;
;
am folosit faptul ca ![]() .
.
Prin urmare in cazul ![]() sunt posibile doua situatii: sau nici una dintre probleme
nu admite programe, ceea ce reprezinta cea de a treia afirmatie a
teoremei, sau una dintre probleme admite programe si cealalta nu
admite. Teorema este complet demonstrata daca aratam
ca in cea de a doua situatie problema care admite programe are optim
infinit. Presupunem in acest caz ca problema (5) admite programul x0, deci Ax0 ≥ b, x0 ≥ 0.
Aratam acum ca orice vector de forma x=x0+λ
sunt posibile doua situatii: sau nici una dintre probleme
nu admite programe, ceea ce reprezinta cea de a treia afirmatie a
teoremei, sau una dintre probleme admite programe si cealalta nu
admite. Teorema este complet demonstrata daca aratam
ca in cea de a doua situatie problema care admite programe are optim
infinit. Presupunem in acest caz ca problema (5) admite programul x0, deci Ax0 ≥ b, x0 ≥ 0.
Aratam acum ca orice vector de forma x=x0+λ![]() cu λ ≥ 0
este program al problemei (5), iar functia obiectiv tinde la
−∞ de-a-lungul razei x.
cu λ ≥ 0
este program al problemei (5), iar functia obiectiv tinde la
−∞ de-a-lungul razei x.
Intr-adevar, avem:
Ax = Ax0+λA![]() ≥b;
≥b;
c'x=c'x0+λc'
![]() → - ∞
→ - ∞
λ→∞
deoarece c'![]() < b'
< b'![]() ≤ (x0)'A'
≤ (x0)'A'![]() ≤ 0, ceea ce
demonstreaza teorema.
≤ 0, ceea ce
demonstreaza teorema.
Prezentam in continuare trei teoreme ce se
constituie in teoreme necesare si suficiente pentru ca un program ![]() sa fie program optim pentru problema (5).
sa fie program optim pentru problema (5).
Teorema 2. (Teorema ecarturilor complementare). O
conditie necesara si suficienta pentru ca programele ![]() P si
P si ![]() D sa fie programe optime pentru problemele duale (5)
si (7) este:
D sa fie programe optime pentru problemele duale (5)
si (7) este:
![]() . (19)
. (19)
Demonstratie.
Necesitatea. Din faptul ca ![]() P si
P si ![]() D sunt programe optime pentru problemele duale (5) si (7)
rezulta ca
D sunt programe optime pentru problemele duale (5) si (7)
rezulta ca ![]() . Mai departe avem:
. Mai departe avem:
![]()
![]()
![]()
![]()
![]()
![]() , deoarece
, deoarece ![]() ,
, ![]()
si produsul scalar este comutativ.
Suficienta. ![]()
![]()
![]()
![]()
![]()
![]()
![]() si
si ![]() sunt programe optime pentru problemele duale (5) si (7)
sunt programe optime pentru problemele duale (5) si (7)
Observatie. Conditiile (necesare si suficiente) din teorema ecarturilor complementare se exprima, in detaliu, astfel:
![]() ;
;
![]() ,
,
sau
![]() ;
;
![]() ,
,
de unde rezulta ca:
![]() ;
;
![]()
si
![]() ;
;
![]() ,
,
ceea ce exprima faptul ca pentru doua programe optime duale, daca una dintre restrictii este satisfacuta ca inegalitate stricta, atunci valoarea variabilei duale corespunzatoare este nula, sau daca una dintre valorile variabilei este strict pozitiva, atunci restrictia duala corespunzatoare este satisfacuta ca egalitate. De aici provine si denumirea de teorema a ecarturilor complementare.
Teorema 3.
(Kuhn-Tucker). Conditia necesara si suficienta pentru ca ![]()
![]() Rn
Rn![]() sa fie program optim al problemei (5) este sa
existe
sa fie program optim al problemei (5) este sa
existe ![]() Rm astfel ca:
Rm astfel ca:
![]() ,
, ![]() ,
, ![]() ; (20)
; (20)
![]() ,
, ![]() ,
, ![]() . (21)
. (21)
Demonstratie. Conditiile
teoremei sunt echivalente cu conditiile ![]() P si
P si ![]() D si cu conditiile din teorema ecarturilor
complementare.
D si cu conditiile din teorema ecarturilor
complementare.
Rezultatul urmator se bazeaza pe conceptul de functie a lui Lagrange (sau lagrangeian) asociata (asociat) problemei de programare liniara (5).
Definitia 2. Se numeste lagrangeian asociat problemei de programare liniara (5) functia:
![]()
definita prin:
![]() . (22)
. (22)
Variabilele duale se mai numesc si multiplicatori Kuhn-Tucker sau multiplicatori ai lui Lagrange prin analogie cu problema extremelor cu legaturi.
Teorema 4. (Teorema lagrangeianului).
Conditia necesara si suficienta pentru ca ![]() sa fie program optim al problemei (5) este sa
existe
sa fie program optim al problemei (5) este sa
existe ![]() astfel incat punctul (
astfel incat punctul (![]() ) sa fie punct-sa pentru lagrangeianul
) sa fie punct-sa pentru lagrangeianul ![]() , adica sa fie indeplinita dubla inegalitate:
, adica sa fie indeplinita dubla inegalitate:
![]() .
.
Demonstratie. Necesitatea. Daca ![]() este program optim al problemei (5), atunci in baza teoremei
Kuhn-Tucker exista
este program optim al problemei (5), atunci in baza teoremei
Kuhn-Tucker exista ![]() astfel incat sa
fie indeplinite conditiile:
astfel incat sa
fie indeplinite conditiile:
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() .
.
Din conditiile ecarturilor rezulta ca:
![]()
si impreuna cu celelalte conditii rezulta:
![]()
![]() .
.
Suficienta. Din prima inegalitate de punct-sa rezulta:
![]()
alegem ![]() si rezulta <ai,
si rezulta <ai,
![]() >-bi≥0
>-bi≥0 ![]() , ai -
vectorul linie i al matricei A, deci A
, ai -
vectorul linie i al matricei A, deci A![]() ≥b, prin urmare
≥b, prin urmare ![]() este program al problemei (5).
este program al problemei (5).
Procedam analog cu cea de a doua inegalitate de punct-sa si rezulta:
![]()
luam ![]() si rezulta cj-<
si rezulta cj-<![]() , aj> ≥ 0,
, aj> ≥ 0, ![]() , adica
, adica ![]() (aj este
vectorul coloana j al matricei A), prin urmare
(aj este
vectorul coloana j al matricei A), prin urmare ![]() este program al problemei (7).
este program al problemei (7).
Pentru cazul particular x = 0 si u = 0, inegalitatile de punct-sa devin:
![]() .
.
Fiind
adevarata si inegalitatea contrara ![]() rezulta ca
rezulta ca ![]() , deci in baza lemei 2 programele
, deci in baza lemei 2 programele ![]() P si
P si ![]() D sunt programe optime pentru problemele (5), respectiv (7).
D sunt programe optime pentru problemele (5), respectiv (7).
Prezentam in finalul acestui paragraf un rezultat care evidentiaza pe de o parte faptul ca este posibil sa se rezolve simultan problemele ce constituie un cuplu de probleme de programare liniara duale si pe de alta parte constituie un element care contribuie la fundamentarea algoritmului simplex-dual.
Consideram de aceasta data problema de programare liniara sub forma standard (23):
min (z = c'x)
Ax = b (23)
x ≥ 0
si duala sa (24):
max (w = b'u)
A'u ≤ c (24)
u - oarecare.
Teorema 5. O conditie suficienta (si necesara daca problema (23) este nedegenerata) pentru ca o baza B din matricea A sa fie baza optima este ca sa fie indeplinite urmatoarele conditii:
B-1b≥0; (25)
(cB)'B-1A - c'≤0. (26)
In aceasta situatie programele optime ale problelor duale (23), (24) sunt:
xB = B-1b; xS = 0,
respectiv
(uB)' = (cB)'B-1.
Demonstratie. Este de remarcat
faptul ca vectorii ![]() si uB definiti mai sus sunt
programe optime pentru problemele (23) si respectiv (24), deoarece sunt
programe pentru cele doua probleme , iar valorile functiilor obiectiv
coincid, adica:
si uB definiti mai sus sunt
programe optime pentru problemele (23) si respectiv (24), deoarece sunt
programe pentru cele doua probleme , iar valorile functiilor obiectiv
coincid, adica:
(cB)'xB = (cB)'B-1b = (uB)'b.
Daca problema (23) este nedegenerata conditia (26) este si necesara pentru optimalitatea bazei B deoarece daca (cB)'B-1ak - ck > 0 (adica zk -ck > 0) atunci, prin introducerea variabilei xk in baza, functia obiectiv scade strict cu valoarea:
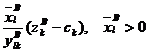 .
.
Teorema precedenta poate fi reformulata, daca definim conceptele de baza admisibila si baza dual-admisibila.
Definitia 3. (i). O baza B care satisface conditia (25) se numeste admisibila (deoarece ii corespunde un program de baza al problemei (23), xB = B-1b, xS = 0);
(ii). O baza B care satisface conditia (26) se numeste dual-admisibila (deoarece ii corespunde un program de baza al problemei duale (24), uB = (cB)'B-1).
Cu aceste elemente, teorema precedenta afirma faptul ca o baza B este optima daca si numai daca este simultan admisibila si dual-admisibila.
Observatii . (i). Daca matricea A contine o matrice unitate Im, atunci la fiecare iteratie simplex in aceste coloane se gaseste inversa bazei curente, adica B-1; in particular in tabelul simplex optim regasim inversa bazei optime. In aceste conditii observam ca in acest tabel regasim si programul optim al problemei duale (26).
(ii). Daca ne referim la cuplul de probleme duale (5), (6) atunci forma standard echivalenta este Ax - y = b, y ≥ 0, daca B este baza optima atunci programul optim al problemei duale (6) reprezinta elementele luate cu semn schimbat, din ultima linie a tabelului simplex optim, situate in coloanele corespunzatoare variabilelor ecart zi,
zi - cei = (uB)'i = - [(cB)'B-1]i