
|
|
|
REGRESIA LINIARA MULTIPLA
Tema 1 - Regresia liniara simpla
Prin aceasta tema voi analiza legatura care exista intre deficitul bugetar, rata dobanzii, rata inflatiei si veniturile publice. Voi porni de la ipoteza ca legatura dintre aceste variabile este una de tip liniar, deci pentru analiza voi folosi o regresie liniara multipla.
Pornind de la realitatea economica, voi considera deficitul bugetar ca fiind variabila dependenta.
Rata dobanzii influenteaza negativ deficitul bugetar, deoarece cu cat deficitul este mai mare, statul se va imprumuta mai scump pentru acoperirea deficitului respectiv.
O crestere a ratei inflatiei (deci o crestere a preturilor) conduce la marirea deficitului bugetar (accentuarea decalajului dintre venituri si cheltuieli).
Veniturile bugetare influenteaza intr-o masura importanta deficitul bugetar (acesta din urma determinandu-se ca diferenta intre veniturile bugetare si cheltuielile bugetare). Avand in vedere ca majoritatea tarilor inregistreaza deficit bugetar (si nu surplus), daca veniturile bugetare vor creste, cheltuielile tot vor fi mai mari si se va inregistra deasemenea deficit (deci va fi o evolutie in acelasi sens).
Pentru a demonstra ipoteza enuntata, voi folosi urmatoarele date (deficit bugetar, rata dobanzii, rata inflatiei si venituri bugetare pentru) Spania:
AN
Y = Deficit bugetar (ca procent din PIB)
X1 = Rata dobanzii (%)
X2 = Rata inflatiei (%)
X3 = Venituri bugetare (ca procent din PIB
1992
-7.51
11.70
5.20
30.02
1993
-8.06
10.21
4.90
36.23
1994
-7.51
10.00
4.60
38.31
1995
-6.48
11.27
4.60
37.96
1996
-4.86
8.74
3.60
38.35
1997
-3.27
6.40
1.90
38.25
1998
-3.10
4.83
1.80
37.84
1999
-1.31
4.73
2.20
38.43
2000
-0.89
5.53
3.50
38.12
2001
-0.52
5.12
2.80
37.98
2002
-0.29
4.96
3.60
38.41
2003
-0.05
4.13
3.10
38.19
2004
-0.19
4.10
3.10
38.57
2005
1.00
3.39
3.40
39.40
2006
2.00
3.78
3.60
40.40
2007
1.90
4.07
2.80
41.10
Sursa: Eurostat(http://epp.eurostat.ec.europa.eu/portal/page/portal/government_finance_statistics/data/main_tables
Cu ajutorul acestor date voi realiza identificarea unei posibile dependente liniare, cu ajutorul Excel-ului, potrivit ecuatiei de regresie: Y = α + β*X1 + γ*X2 + δ*X3 + eiar rezultatul este:
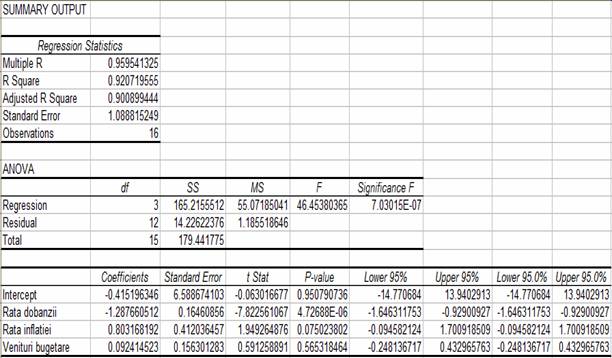
Interpretarea rezultatelor din SUMMARY OUTPUT
Multiple R este un indicator al determinarii modelului si poate avea valori cuprinse intre 0 si 1. In cazul de fata valoarea inregistrata este de 0,959541325 care este mai mare de 0,7 (un prag considerat, peste care putem spune ca modelul corespunde realitatii economice).
Cu cat R2 ia valori mai apropiate de 1, cu atat modelul de regresie ajusteaza mai bine datele din esantion; asadar, interpretarea valorii inregistrate de R Square este ca 92,0719% din variatia totala a variabilei dependente: deficit bugetar (Y) este explicata prin acest model de regresie.
Valoarea coeficientului de determinatie ajustat este 0,9 deci se apropie de 1; el este folosit ca instrument de decizie pentru includerea sau nu a unei noi variabile in modelul de regresie.
Daca toate punctele s-ar afla pe dreapta de regresie, eroarea standard ar fi 0, deci este de preferat ca Standard Error sa fie cat mai aproape de 0 (in cazul de fata este 1,088815).
Interpretarea rezultatelor din primul tabel ANOVA:
Cu ajutorul primului tabel ANOVA se face validarea intregului model de regresie prin intermediul testuli F. Pentru aceasta se construiesc cele doua ipoteze:
H0: model nevalid, cu alternativa
H1: model valid
Valoarea teoretica pentru un prag de semnificatie de 0,05 si 3; si respectiv 12 grade de libertate este F0,05;3;12 = 3,49. Intr-ucat Fcalculat (46,45) este mai mare decat F0,05;3;12 (3,49) iar nivelul de semnificatie al lui F este mai mic de 5%, se respinge ipoteza nula si deci modelul este valid.
Interpretarea rezultatelor din al doilea tabel ANOVA
Acest tabel este format din estimatiile coeficientilor, erorile lor standard, valoarea statisticii t, valoarea p asociata si intervale de incredere 95% pentru fiecare din coeficientii estimati.
Cu ajutorul acestui tabel ANOVA se poate scrie ecuatie de regresie utilizand valorile coeficientilor estimati:
Deficit bugetar = 0,4152 - 1,2877*Rdob + 0,8032*Rinf + 0,0924*Vn_bug ; unde
Rdob = rata dobanzii; Rinf = rata inflatiei; Vn_bug = venituri bugetare
Dupa ce am validat modelul ca intreg, voi analiza din nou validitatea modelului, luand in considerare fiecare coeficient in parte, prin intermediul testului t.
Astfel, se aleg cele doua ipoteze:
H0: coeficientul nu este semnificativ diferit de 0 (deci este egal cu 0)
H1: coeficientul este semnificativ diferit de zero
Pentru un prag de semnificatie de 5-10%, daca valoarea p asociata coeficientului estimat este sub acest prag de 10%, se poate afirma ca eroarea care se face prin respingerea ipotezei nule este mica si deci se accepta ipoteza alternativa H1. Daca in schimb, valoarea p inregistrata pentru un coeficient este mai mare de 75-80%, atunci eroarea pe care o fac prin respingerea ipotezei nule este mare si deci trebuie sa accept ipoteza nula. Mai exista o posibilitate, ca valoarea p corespunzatoare coeficientului sa fie in intervalul 0,1-0,8 care este o zona de indecizie si nu ma pot pronunta asupra semnificatiei coeficientului asupra modelului.
Validarea coeficientilor
Pentru termenul liber (intercept) coeficientul este -0,4152 iar valoarea p asociata acestuia este 0,9508 > 0,8 deci as face o eroare mare prin respingerea ipotezei nule deci o accept, ceea ce inseamna ca termenul liber nu are o influenta importanta asupra modelului (coeficientul sau nu este semnificativ diferit de 0. Acest lucru este confirmat si de intervalul de incredere 95% pentru intercept: (-14,7707 ; 13,9403) care il contine pe 0. Modelul de regresie trebuie respecificat, tinand seama de faptul ca termenul liber nu are o influenta semnificativa (voi realiza acest lucru prin intermediul Eviews-ului).
Pentru prima variabila independenta (Rdob) coeficientul este de -1,2876 iar valoarea p asociata este 4,72688E-06 < 0,1 rezulta ca prin respingerea ipotezei nule fac o eraore mica si accept ipoteza H1, conform careia coeficientul Rdob este semnificativ diferit de 0. Intervalul de incredere 95% pentru aceasta variabila este (-1,6463 ; -0,9290).
Pentru rata inflatiei, coeficientul este de 0,8032 iar valoarea p asociata este de 7,5023% < 10% deci se poate respinge ipoteza nula si se accepta ipoteza H1, coeficientul ratei inflatiei fiind semnificativ diferit de 0. Intervalul de incredere 95% pentru aceasta variabila este
(-0,0946 ; 1,7009).
Coeficientul veniturilor bugetare este de 0,0924 iar valoarea p asociata este 0,5653, valoare ce se situeaza in zona de indecizie deci nu se poate preciza daca accept ipoteza nula sau ipoteza alternativa. Se poate respinge ipoteza nula, prin asumarea unui risc de 56,53% (p-value, situat in zona de indecizie) si se poate accepta astfel ipoteza H1 conform careia coeficientul Vn_bug este diferit de 0; se poate manifesta insa riscul de gradul I. Intervalul de incredere 95% pentru aceasta variabila este (-0,2418 ; 0,4329).
Alte rezultate pe care le ofera Excel sunt reprezentate de RESIDUAL OUTPUT si de PROBABILITY OUTPUT:
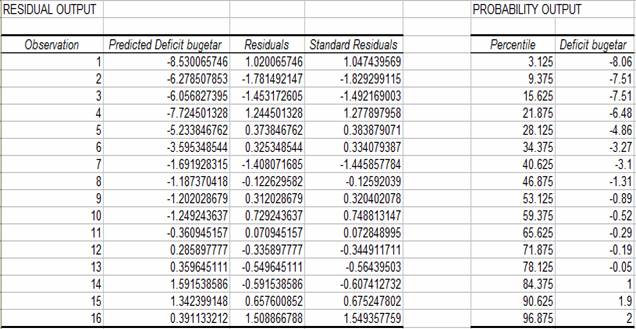
In coloana Predicted Deficit bugetar sunt redate valorile ajustate pentru variabila dependenta. Rzidurile din urmatoarea coloana se pot calcula ca diferenta intre valorile initiale ale variabilei dependente (deficit bugetar) si estimatiile sale. Se observa ca rezidurile au atat valori pozitive cat si valori negative, iar suma lor este 0.
Rezidurile standardizate se pot obtine conform formulei:
Standard Residuals=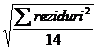
Dupa analiza rezultatelor obtinute in Excel iar in continoare voi analiza modelul de regresie liniara multipla prin intermediul programului Eviews, folosind metoda celor mai mici patrate (OLS). Dupa importul datelor din Excel si tastarea comenzii: ls def_bug c rdob rinf vn_bug rezultatul este:
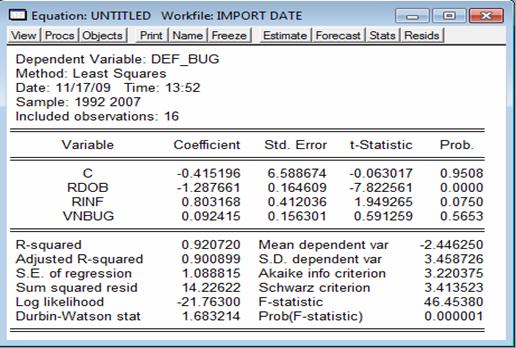
Ecuatia de regresie scrisa cu coeficientii estimati arata astfel:
DEF_BUG = -0,415196 - 1,287661*RDOB + 0,803168*RIBF + 0,092415*DEFBUG
Se observa ca rezultatele din Eviews le confirma pe cele din Excel (sunt identice). Dupa cum am precizat si in cazul Excel-ului, termenul liber are o probabilitate p mare ( peste 0,95) deci se impune eliminarea termenului liber din model.
Rezultatele modelului de regresie liniara multipla, fara termen liber, sunt:
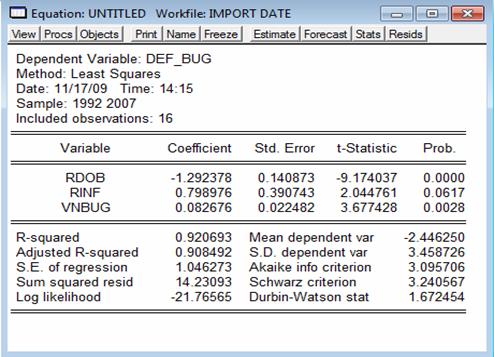
In acest caz, ecuatia de regresie poate fi scrisa astfel:
DEF_BUG = -1,292378*RDOB + 0,798976*RINF + 0,082676*VNBUG
Rezultatele obtinute in urma eliminarii termenului liber sunt asemanatoare cu cele obtinute initial; se observa totusi imbunatatiri: eroarea standard a regresie s-a micsorat si cel mai important, valoarea p, corespunzatoare veniturilor bugetare, a devenit 0,28% < 10% deci se respinge ipoteza nula, acceptand faptul ca veniturile bugetare au un coeficient semnificativ diferit de 0 (fata de situatia initiala, cand valoarea p pentru aceasta valoare era de 56,53% si era deci situata in zona de indecizie).
Statistica Akaike a celui de al doilea model (3,0957) este mai mica decat cea a modelului initial (3,2204) deci se poate afirma ca cel de al doilea model (fara termen liber) corespunde mai bine realitatii economice (se stie ca este mai bun modelul care are statistica Akaike mai mica) deci in continuare se va lucra pe acest ultim model, fara termen liber.
Interpretarea economica
Modelele de regresie se folosesc pentru a estima modificarile suferite de variabila dependenta, determinata de modificarile uneia dintre variabilele independente.
Daca rata dobanzii se modifica cu un procent, in conditiile in care celelalte variabile independente raman constante, deficitul bugetar se va modifica in sens opus (din cauza semnului minus) cu 1,29%.
Daca rata inflatiei se modifica cu un procent, in conditiile in care celelalte variabile independente raman constante, deficitul bugetar se modifica in acelasi sens cu 0,79%.
Daca veniturile bugetare se modifica cu un procent, in conditiile in care celelalte variabile independente raman constante, deficitul bugetar se modifica in acelasi sens cu 0,08%.
Mai departe voi face testele specifice pentru a verifica autocorelarea, homoscedasticitatea si normalitatea.
Ipotezele modelului liniar de regresie. Testare si tratare
I. Ipoteza privind independenta erorilor
1. Analiza autocorelarii de ordinul I
Ecuatia corelarii rezidurilor este:
et = ρ*et-1 + vt
Se vor folosi reziduurile (din coloana RESID, pe care le-am salvat prin comanda:
genr R_EQ1 = RESID
Pentru a verifica corelarea intre reziduri si rezidurile intarziate cu o perioada aplicam comanda: scat R_EQ1(-1) R_EQ1 si apare graficul:
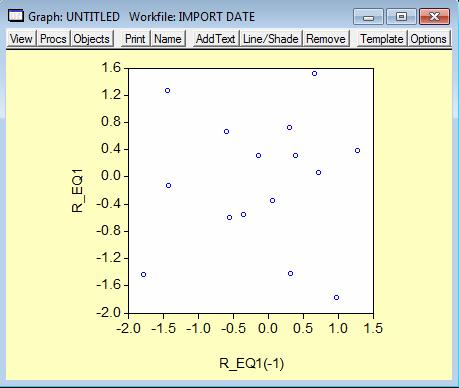
Erorile par a fi dispersate aleator insa necorelarea lor nu este evidenta, deci voi continua cu estimarea parametrului ρ din modelul de corelare a erorilor: et = ρ*et-1 + vt , prin comanda: ls R_EQ1 R_EQ1(-1) si rezulta:
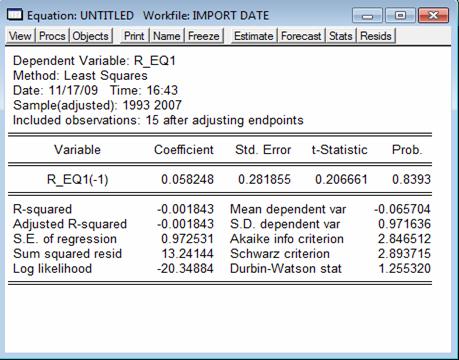
Pentru parametrul ρ s-a estimat un coeficient de 0,058 insa pentru o valoare p de 83,94% care este mai mare decat 80% deci trebuie acceptata ipoteza nula (conform careia coeficientul nu este semnificativ diferit de 0) deci ρ = 0, ceea ce inseamna ca erorile nu prezinta autocorelare de ordinul 1.
Testul Durbin-Watson
Autocorelarea erorilor se poate determina si cu ajutorul testului Durbin-Watson. Valoarea statisticii Durbin-Watson se obtine prin comanda: genr DW = 2*(1-c(1)) iar rezultatul este 1,883503. Statistica Durbin-Watson este tabelata, valorile ei depinzand de nivelul de semnificatie (pe care il voi considera 5%), de numarul de observatii din esantion (16 observatii) si de numarul variabilelor de influenta din modelul de regresie (sunt 3 variabile de influenta). Cele doua ipoteze sunt: H0 : ρ=0 si H1 : ρ diferit de 0.
Statistica Durbin-Watson pentru un nivel de semnificatie precizat are doua valori critice: dl si du ce se obtin din tabele. Pentru nivelul de semnificatie considerat de 5%, 16 observatii si 3 variabile de influenta valorile critice sunt: dl = 0,98 si du = 1,54. Regiunile de respingere a ipotezei nule sunt:
daca DW apartine [0 ; dl] = [0 ; 0,98] se respinge ipoteza nula iar autocorelatia este pozitiva;
daca DW apartine [4- dl ; 4] = [4-0,98 ; 4] se respinge ipoteza nula iar autocorelatia este negativa;
Daca DW apartine [du ; 4- du] = [1,54 ; 2,46] nu se confirma prezenta autocorelatiei; valoarea statisticii Durbin-Watson din cazul de fata este 1,88 deci se incadreaza in acest interval si se accept ipoteza nula (ρ=0), erorile fiind necorelate.
Rezidurile, in functie de Actual, Fitted si Residual sunt reprezentate in tabelul urmator:
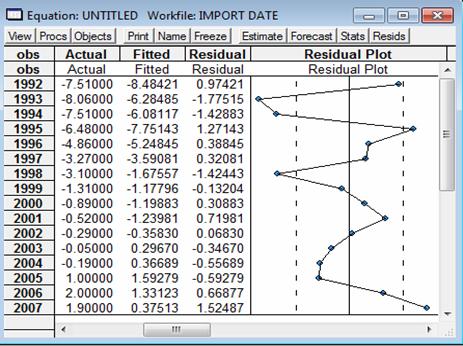
Iar reprezentarea lor grafica arata astfel:
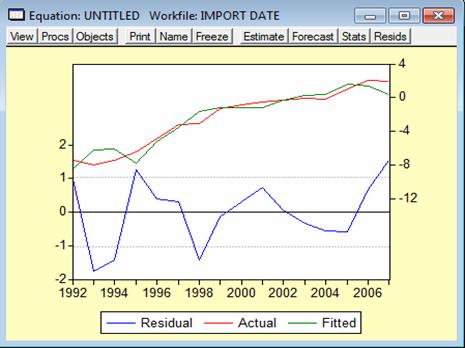
Graficul rezidurilor de mai sus este asemanator cu un grafic al unui model valid erori necorelate.
In concluzie, s-a demonstrat atat prin estimarea coeficientului de corelatie cat si prin statistica Durbin-Watson ca erorile de ordinul 1 sunt necorelate.
2. Analiza autocorelarii de ordin superior
Se poate face prin doua metode:
a. Prin comanda: ls def_bug rdob rinf vnbug ar(1) ar(2) ar(3);ceea ce are ca efect output-ul Eviews:
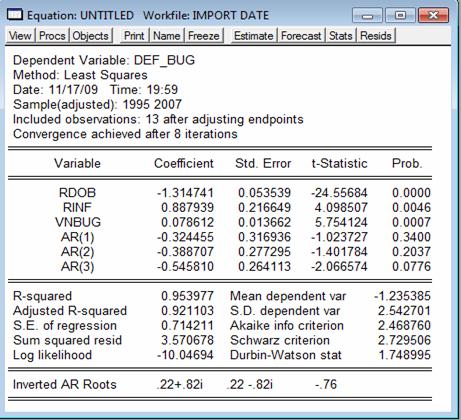
Dintre cele trei variabile autoregresive, cea de ordinul 3 pare a nu avea coeficientul semnificativ diferit de 0 (valoarea p asociata fiind 7,76%). AR(1) si AR(2) au probabilitati asociate situate in zona de incertitudine deci nu se poate aprecia cu ajutorul acestui test daca exista sau nu erori autocorelate de ordin superior.
b. Cu ajutorul testului Breuch-Godfrey
Se presupune ca intre erorile modelului exista o autocorelatie de ordin s (s mai mic sau egal cu 3) deci se poate scrie ecuatia de autocorelatie a erorilor:
et = ρ1*et-1 + ρ2*et-2 + +ρs*et-s + vt
Pentru a evalua prezenta unei autocorelatii de ordin "s" se enunta cele doua ipoteze:
H0 : ρ1 = 0 si ρ2 = 0 si ρ3 = 0 ; cu ipoteza alternativa
H1 : ρ1 diferit de 0 si ρ2 diferit de 0 si ρ3 diferit de 0
Efectuand in Eviews Residual Tests -> Serial Correlation LM Tests cu doua intarzieri, se obtin urmatoarele rezultate:
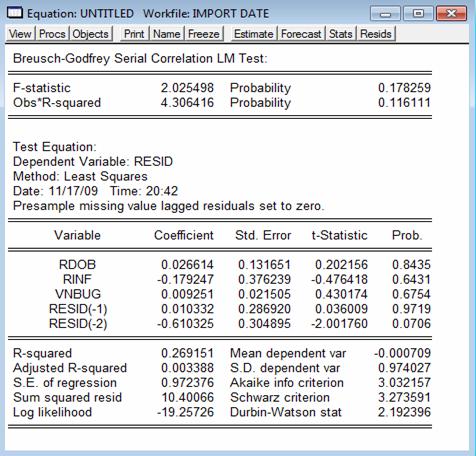
Statistica F are o valoare de 2,025 insa valoarea p de 0,1783 este situata in zona de incertitudine si deci nu putem afirma nimic despre modelul de regresie.
Dintre parametrii modelului, singurul care are probabilitatea corespunzatoare pentru a fi semnificativ diferit de 0 pare sa fie RESID(-2) ; valoarea p a sa de 7,06% fiind mai mica decat 10%. Aceasta se poate interpreta prin faptul ca modelul de regresie prezinta autocorelare a erorilor de ordinul 2.
Coeficientul de determinatie reda o legatura slaba intre parametrii modelului, valoarea sa de 0,2691 fiind mai aproape de 0 decat de 1.
Coeficientul de determinatie ajustat tinde spre zero, semn ca variabilele RESID(-1) si RESID(-2) nu trebuiau introduse in model.
Singura statistica buna este Durbin-Watson a carei valori de 2,1924 se apropie de 2.
Din graficul urmator, ce cuprinde si tabelul cu valori observate, ajustate si reziduri, se poate observa ca erorile nu indeplinesc conditiile, graficul Residual Plot depasind liniile punctate.
II. Verificarea homoscedasticitatii
Se refera la faptul ca erorile trebuie sa fie independente statistic si sa aiba aceeasi varianta. Ipoteza homoscedasticitatii se verifica cu ajutorul testului lui White. In Eviews acesta se aplica prin comanda Residual Tests->White Heteroskedasticity iar apoi se face validarea modelului obtinut.
Output-ul din Eviews pentru testul lui White este:
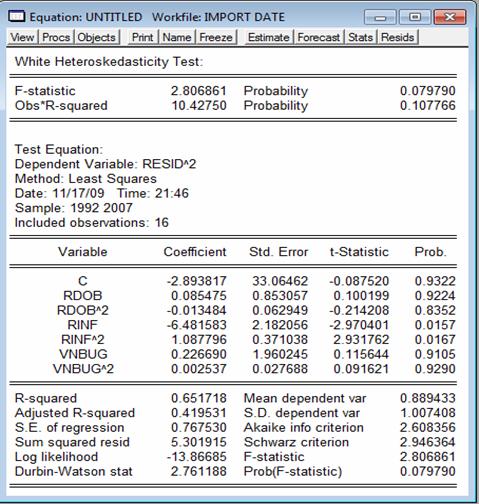
Pentru validarea modelului ca intreg ne folosim de statisica F care este de 2,8068 iar valoarea p asociata de 7,979% < 10% ne permite sa respingem ipoteza nula si sa acceptam ipoteza alternativa deci ca cel putin un termen al modelului este diferit de 0. Putem afirma astfel ca homoscedasticitatea este afectata deci este prezent fenomenul de heteroscedasticitate.
In ceea ce priveste fiecare termen in parte al modelului, se observa faptul ca pentru rata inflatiei si pentru patratul ratei inflatiei valoarea p asociata este de sub 5% ceea ce inseamna respingerea ipotezei nule privind egalitatea cu 0 a dispersiilor, cu o eroare de 1,6% si se poate concluziona ca este violata ipoteza de homoscedasticitate.
Pentru a incerca sa corectez heteroscedasticitatea, voi construi un model in care voi imparti variabila dependenta (deficit bugetar) la cel mai semnificativ dintre variabilele independente (rata dobanzii). Am construit in Eviews modele de regresie simpla in care am utilizat variabila dependenta Y (deficit bugetar) pe care am impartito la variabila independenta, iar ca variabila independenta 1/X am folosit pe rand, cele trei variabile independente (rata dobanzii, rata inflatiei si venituri bugetare). In urma celor trei regresii liniare simple construite a rezultat ca cel mai bun model il reprezinta cel ce contine rata dobanzii.
Astfel, in noul model pe care il voi construi variabila dependenta o voi imparti la rata dobanzii, iar ca variabile independente voi utiliza inversul variabilelor independente initiale (1/rdob, 1/rinf, 1/vnbug). Modelul rezultat arata astfel:
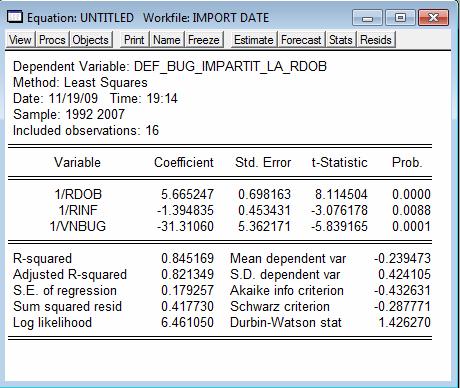
Se observa o valoare buna a coeficientului de determinatie de 84,52%. Toti coeficientii (dupa eliminarea termenului liber, a carui coeficient nu era semnificativ diferit de 0) sunt semnificativi statistic, ceea ce ne conduce la un model valid, din perspectiva fiecarui parametru in parte.
In urma aplicarii testului White pentru verificarea homoscedasticitatii rezulta output-ul urmator:
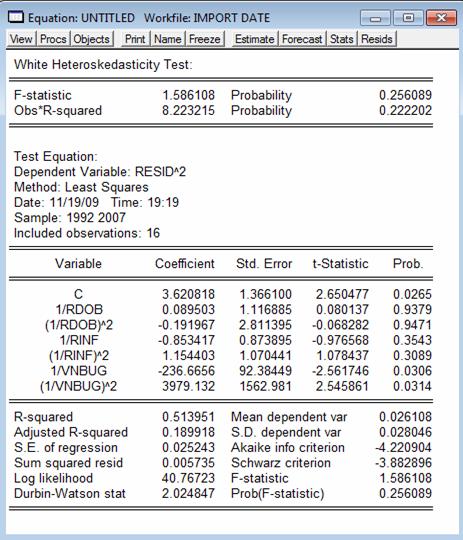
Coeficientul de determinatie este mic, in jurul valorii de 50%.
Pentru validarea modelului, statistica F este de 1,5861 dar are o probabilitate de 25,6% situata in zona de incertitudine deci nu se poate preciza.
Cele doua ipoteze considerate sunt: H0 : toti coeficientii modelului sunt 0 si se accepta deci ipoteza nula de homoscedasticitate, cu alternativa H1 : heteroscedasticitate.
In ceea ce priveste fiecare parametru in parte, pentru termenul liber (C), 1/VNBUG si /VNBUG2 au probabilitati asociate de sub 5%, ceea ce ne permite sa consideram acesti parametri ca fiind diferiti de 0, adica trebuie sa respingem ipoteza nula, de homoscedasticitate, in concluzie modelul prezinta heteroscedasticitate.
III. Ipoteza normalitatii
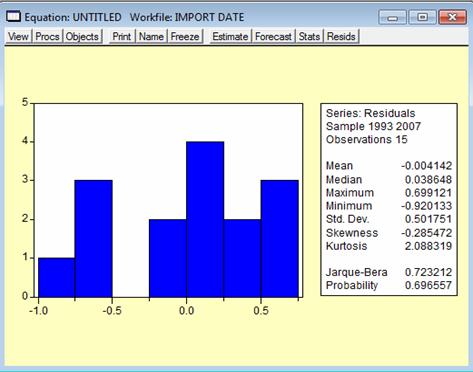
Verificarea normalitatii se face in Eviews prin aplicarea comenzii Residual Tests -> Histogram - Normality Test in urma careia rezulta urmatorul output:
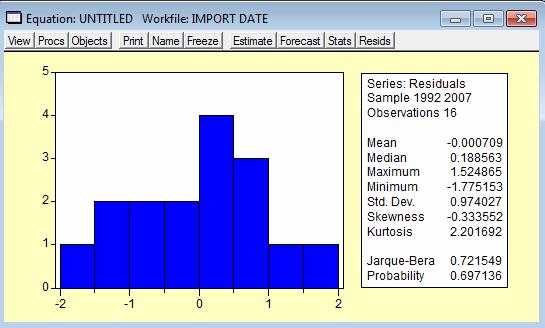
Se construiesc cele doua ipoteze astfel:
H0 : skewbess = 0 , kurtosis = 3 deci repartitia este normala
H1 : skewness diferit de 0 sau kurtosis diferit de 0 deci repartitia nu este normala
Iar in functie de statistica testului Jarque-Bera si de probabilitatea asociata se accepta sau se respinge ipoteza nula. In cazul de fata valoarea Jarque-Bera este de 0,721549 insa probabilitatea sa de 0,69 se situeaza in zona de incertitudine si nu se poate aprecia normalitatea modelului. Pentru o imbunatatire se recomanda marirea numarului de observatii, daca este posibil.
Pentru o repartitie normala, skewness-ul ar fi trebuit sa fie 0 (fara de -0,33 cat este in model) iar kurtosis-ul ar fi trbuit sa fie 3 (fata de valoarea de 2,2 inregistrata ceea ce reprezinta o abatere destul de mare).
In incercarea de a corecta modelul, am luat in considerare mai intai valorile anterioare inregistrate atat de variabila dependenta cat si de variabilele independende. Modelul obtinut este valid din punctul de vedere al testului F, de validare a intregului model insa la validarea fiecarui parametru, singura variabila a carei coeficient a reiesit diferit semnificativ de 0 a fost deficitul bugetar din anul anterior, restul probabilitatilor pentru celelalte variabile situandu-se in zona de incertitudine, conform output-ului urmator:
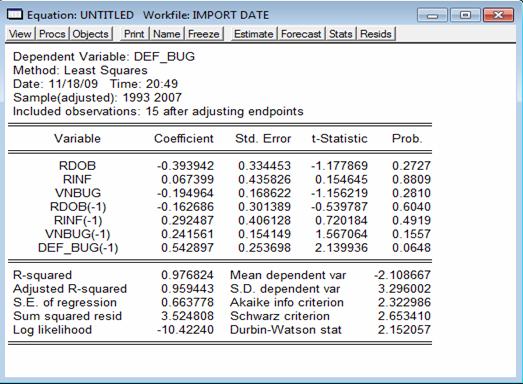
In urma efectuarii testului de normalitate, valoarea Jarque-Bera de 0,72 are o probabilitate asociata de 0,69 valoare situata tot inb zona de indecizie deci nu se poate respinge sau accepta normalitatea (insa histograma primului model arata mai "normala" decat a celui de al doilea).
Intr-ucat datele observate pentru variabila dependenta deficit bugetar (def_bug) contin si valori negative, nu se pot logaritma datele pentru a incerca corectarea modelului in acest fel.
BIBLIOGRAFIE
Liliana Spircu, Roxana Ciumara - "Econometrie", Editura Pro Universitaria, Bucuresti 2007
Vergil Voineagu, Simona Ghita, Emilia Titan, Daniela Todose, Daniel Pele, Radu Serban, Cristina Boboc - "Teorie si practica econometrica", Editura Meteor Press, Bucuresti 2007
http://epp.eurostat.ec.europa.eu/portal/page/portal/eurostat/home/
Cursuri si seminarii trimise de Dumneavoastra