Teorema limitei centrale

Teorema limitei centrale

In exemplele date anterior, am extras esantioane din populatii foarte mici de valori. Problema este ca, daca am avea populatii atat de mici, atunci nu am avea nevoie sa facem studii pe baze de esantion ci am putea investiga fara dificultate intreaga populatie. In realitate populatiile care fac obiectul de interes al cercetarilor de psihologie sunt prea mari pentru a fi accesibile in intregimea lor. Si chiar daca ar fi accesibile, ar fi prea costisitor sa fie investigate integral. In acest caz se pune problema masurii in care putem estima caracteristicile statistice ale distributiei populatiei (media, abaterea standard) pe baza acelorasi indicatori calculati doar la nivelul unui anumit esantion, selectat pentru studiu. 

Solutia acestei probleme rezida in teorema limitei centrale care certifica doua adevaruri statistice fundamentale:

1. Cu cat numarul esantioanelor realizate dintr-o populatie (tinzand spre infinit) este mai mare, cu atat media distributiei de esantionare se apropie de media populatiei. 
2. Distributia mediei de esantionare se supune legilor curbei normale, chiar si atunci cand distributia variabilei la nivelul intregii populatii nu are un caracter normal, cu conditia ca volumul esantioanelor sa fie  "suficient de mare". Cu alte cuvinte, distributia mediei de esantionare se apropie de distributia normala, cu atat mai mult cu cat volumul esantionului este mai mare.

Utilitatea teoremei limitei centrale consta in faptul ca ea permite fundamentarea inferentelor statistice fara a ne preocupa prea mult de forma distributiei variabilei la nivelul populatiei. Este de ajuns sa utilizam un esantion "suficient de mare" pentru a ne putea asuma presupunerea unei distributii normale la nivelul mediei de esantionare.

Intrebarea care se pune este, insa, cat de mare trebuie sa fie un esantion pentru a putea fi considerat "suficient de mare"? Fara a intra in amanunte, vom spune ca, daca esantionul de referinta cuprinde cel putin 30 de subiecti, teoria statistica accepta ca avem o distributie normala a mediei de esantionare. Acest numar (30), care nu are nimic magic in el, este utilizat de obicei pentru constituirea esantioanelor minime de cercetare. Pe aceasta baza orice esantion avand cel putin 30 de valori este considerat "esantion mare" in timp ce orice esantion cu mai putin de 30 de valori este considerat "esantion mic".

Sa precizam trei aspecte deosebit de importante atunci cand ne plasam in contextul teoremei limitei centrale. In acest caz esantioanele:

a.     sunt constituite pe baze absolut aleatoare;

b.     se considera independente unele de altele (formate din valori distincte);

c.      toate au acelasi volum

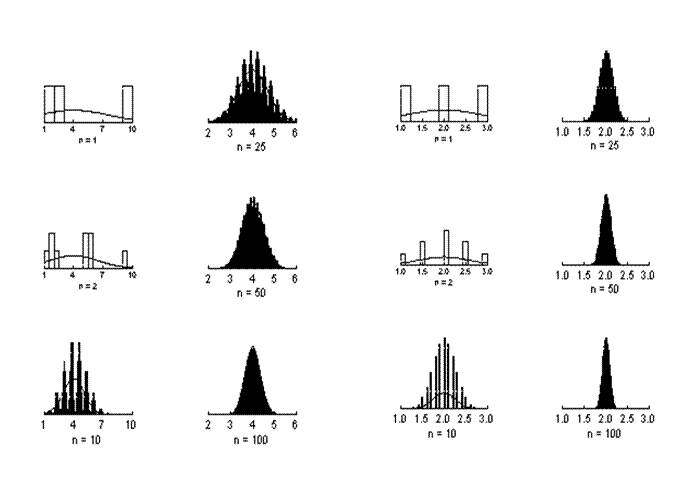
Pentru a intelege mai bine modul in care se distribuie mediile de esantionare vom apela la un set de imagini obtinute prin simulare computerizata. Au fost luate in considerare distributiile a doua variabile. Prima, cea din stanga, nu are un caracter normal in timp ce a doua, din dreapta, are un caracter normal. Pentru fiecare dintre ele au fost simulate distributii de esantionare pentru esantioane progresive ca volum: 2, 10, 25, 50 sau 100 de valori.  Figurile de mai jos ne ajuta sa desprindem doua concluzii:

1. indiferent de forma distributiei variabilei, distributia de esantionare tinde spre curba normala, pe masura ce volumul esantionului creste
2. daca distributia variabilei la nivelul populatiei este normala, atunci distributia de esantionare atinge o forma normala pentru esantioane de volum mai mic.

In concluzie, distributia mediei de esantionare are o evolutie diferita de distributia valorilor individuale ale unei caracteristici. Chiar si atunci cand acestea din urma nu se distribuie dupa regulile curbei normale, mediile esantioanelor tind spre o distributiei normala daca volumul lor este suficient de mare. Marimea esantionului trebuie sa fie de cel putin 30 de valori pentru a avea incredere ca teorema limitei centrale se verifica. Dar chiar si esantioane de volum mai mic pot avea medii ce se plaseaza pe o distributie normala, daca provin din populatii normale. Din pacate, forma distributiei la nivelul populatiei nu este aproape nici o data cunoscuta. In acest caz singurul lucru pe care il putem face este sa utilizam, ori de cate ori ne putem permite, "esantioane mari", adica de cel putin 30 de valori, si chiar mai mari, daca acest lucru este posibil. Cu toate acestea, asa cum vom vedea mai departe, exista solutii statistice si pentru esantioane mai mici de 30 de valori.

Notele standardizate z pentru esantioane (grupuri)

Ne vom referi acum la exemplul anterior, in care avem cinci esantioane extrase dintr-o populatie de 10 valori. Daca avem media distributiei de esantionare si abaterea standard a acesteia (calculata ca eroare standard a mediei, cu formula 3.1), atunci putem exprima media unui esantion oarecare, ca scor standardizat z, intr-o maniera similara cu scorul standardizat z pentru o valoare oarecare. Rostul acestei transformari ar fi acela de a vedea in ce masura media esantionului de studiu se indeparteaza de media populatiei de referinta. Cu alte cuvinte, in ce masura rezultatul obtinut pe esantion este unul "obisnuit" (mai aproape de media populatiei) sau unul "neobisnuit" (mai indepartat de media populatiei).

Formula de calcul este foarte asemanatoare cu formula lui z pentru valori individuale:

(formula 3.2)

unde m este media esantionului, m este media de esantionare care, la limita, tinde spre media populatiei, iar s_m este eroarea standard a mediei de esantionare.

Daca presupunem ca obiectul de studiu este esantionul 1, atunci putem calcula mai intai eroarea standard a mediei (abaterea standard a distributiei de esantionare), astfel:

In exemplul nostru, limitat la o populatie cunoscuta, am putut calcula abaterea standard a populatiei (σ=3.02) dar, pentru situatii reale, cu populatii nelimitate, acest lucru nu este posibil. In astfel de cazuri se accepta faptul ca abaterea standard a populatiei este "suficient de bine reprezentata" de abaterea standard a esantionului extras din aceasta. Ca urmare, daca cunoastem abaterea standard a populatiei, putem utiliza in formula erorii standard a mediei, abaterea standard a esantionului (in cazul nostru s₁₌5.65 in loc de s=3.02).

Mai departe, nota standard z pentru esantionul 1, se calculeaza astfel:

unde m este media esantionului 1, m este media populatiei, iar s_m este eroarea standard a mediei.

Exemplu:

Sa presupunem ca, la un examen de cunostinte de statistica, o grupa de 45 de studenti obtine un scor mediu de m=28.5 puncte. Presupunand ca media pe populatia studenteasca care a mai dat acest examen (calculata de-a lungul anilor anteriori) este m=27.3, cu o abatere standard s=8.2, trebuie sa aflam care este performanta performantei grupei respective transformata in note z.

Calculam mai intai abaterea standard a mediei:

Calculam apoi scorul z pentru grup:

Daca vrem sa stim unde se plaseaza performanta grupului nostru pe o curba normala, atunci ne uitam pe tabela notelor z si gasim, in dreptul scorului z=0.98, valoarea tabelara 0.3365. Aceasta poate fi interpretat in mai multe feluri. De exemplu, putem spune ca procentul performantelor posibile peste nivelul grupului nostru este 50%-33%, adica 17%. Sau, in termeni probabilistici, putem sune si ca: "probabilitatea de a avea o grupa (un esantion, de aceeasi marime) care sa obtina un scor mai bun la un examen de statistica (cu aceleasi intrebari) este de 0.17".