|
|
|
Determinarea sumei Minkowski dintre un poligon convex si unul oarecare
Se considera o multime de obstacole rigide si inpenetrabile modelate sub forma unor poligoane ,o pozitie initiala s,una finala t si un robot(care in cazul nostru este un poligon convex).Pornind cu robotul din s sa se deplaseze printre obstacole astfel incat sa ajungem in starea finala t.Deplasarea printre obstacole se face fara coliziuni(configuratie in care intersectia dintre obstacol si robot contine puncte in interiorul obstacolului).
In cazul nostru (cand robotul este un poligon convex) miscarea este mult mai complicata.Ar trebui sa efectuam o rotatie ,dar ne vom limita la o translatie.Trebuie ,deci,sa marim obstacolele cu ajutorul sumei Minkowski.
Vom prezenta programul care efectueaza aceasta suma dupa demonstratia geometrica necesara.
Demonstratie geometrica
![]()
Fie
A si B doua multimi de puncte din plan;daca stabilim un sistem de coordonate
atunci punctele pot fi vazute ca vectori in acel sistem de coordonate.Definim
suma multimilor A si B in cel mai natural mod posibil:
,unde x+y este suma vectoriala a celor doua puncte.Aceasta suma este cunoscuta ca suma Minkowski a celor doua multimi.
![]()
Va
fi mai usor sa intelegem sensul acestei idei abstracte considerand suma
Minkowski a unui punct x cu o multime B:
![]()
Aceasta este doar o copie a multimii B
translatata de vectorul x,fiecare punct yIB fiind miscat cu x.Deci,
este reuniunea copiilor multimii B,una pentru fiecare xIA.
Acum sa presupunem ca multimea A este un poligon P,iar multimea B este un disc R centrat in origine.Atunci P R poate fi vazut ca multe copii ale lui R translatat cu x ,pentru toti xIP.
Cum R este centrat in origine, x R va fi centrat.Deci P R echivaleaza cu plasarea unei copii a lui R centrata in fiecare punct al lui P.Acum ar trebui sa fie clar ca P R este chiar poligonul (obstacolul) marit ce il vom nota cu P+.
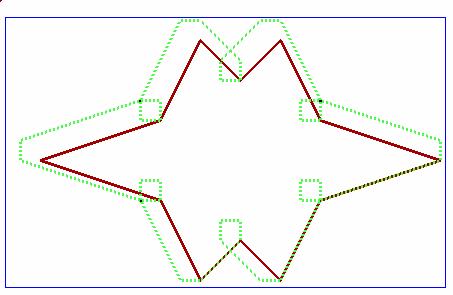
Exemplu:
Fie R un patrat,iar punctul de referinta r sa fie coltul din stanga jos.Consideram unpoligon ca cel din figura de mai jos.Cum R se misca in jurul frontierei lui P ,r traseaza limita(frontiera) lui P+,un obstacol marit care defineste regiunea planului unde r nu poate patrunde.
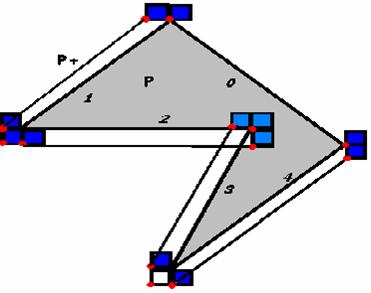
Teorema Fie R o regiune (robotul) si rIR un punct de referinta.Fie P un obstacol.Atunci regiunea P+ = P -R este o multime de puncte interzise lui r din urmatoarele puncte de vedere:
1.Daca R este translatat astel incat r este strict interior lui P+,atunci R penetreaza P.
2.Daca R este translatat astfel incat r se afla pe P+,atunci R atinge P.
3.Daca R este translatat astfel incat r este strict exterior lui P+,atunci R P=
Din convenienta vom lua r ca fiind originea.
Laturile poligonului P+ sunt fie paralele cu laturile lui P ,fie paralele cu laturile robotului(in cazul nostru, cu laturile patratului).
Vom nota laturile patratului astfel:.
Putem vedea in imaginea de mai sus ca am notat laturile poligonului P astfel:.
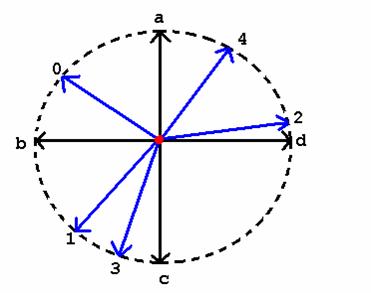
In cele ce urmeaza se va forma diagrama stea a vectorilor astfel:pentru fiecare latura orientata a poligonului P si a poligonului R se considera un punct pe cercul trigonometric astfel incat vectorul de pozitie al acestui punct sa aiba acceasi directie si sens cu latura orientata considerata.
Teorema Daca P are n puncte,iar R are un numar fix(constant) de puncte,atunci suma Minkowski P -R poate fi construita cu o compexitate a a timpului,astfel:
R P Dimensiunea sumei Complexitatea timpului
Convexconvex O(n)O(n)
Convex nonconvex O(n)O(n*nlogn)
Nonconvex nonconvex O(n*n)O(n*nlogn)
#include<stdio.h>
#include<math.h>
#include<stdlib.h>
#include<graphics.h>
#include<conio.h>
#define EXIT_FAILURE1
#define X 0
#define Y 1
#define PMAX 1000
typedef enumbool;
#define DIM 2 /* Dimensiunea punctelor */
typedef int tPointi[DIM];
typedef struct punct tsPoint;
typedef tsPoint *tPoint;
struct punct;
/* primary - daca punctul apartine primului poligon returneaza TRUE,iar daca punctul apartine celui de-al doilea poligon returneaza FALSE */
typedef tsPoint tPointArray[PMAX];
static tPointArray P;
int m;/*Nr. total de puncte din ambele poligoane */
int n; /*Numarul de puncte din primul poligon*/
int s; /*Numarul de puncte din al doilea poligon*/
int aria(tPointi a,tPointi b,tPointi c)
void AddVec(tPointi a,tPointi b,tPointi c)
/* Realizam citirea coordonatelor celor doua poligoane;aflam cei trei contori globali m,n,s,unde m=n+s,returnam un punct de start p0 */
int citire(tPointi p0)
printf('Dati nr de varfuri pt al 2-lea poligon:');
scanf('%d', &s );
if ( n+s > PMAX )
printf('Eroare in citire: > %dn', PMAX), exit(EXIT_FAILURE);
for( i = 0; i < s; i++ )
clrscr();
xmin = xmax = P[0].v[X];
ymin = ymax = P[0].v[Y];
mp = 0;
for (i = 1; i < n; i++)
else
if (P[i].v[Y] == ymax && (P[i].v[X] > P[mp].v[X]))
mp = i;
else
if (P[i].v[Y] < ymin)
ymin = P[i].v[Y];
}
/* Indicele punctului cel mai de sus dreapta din primul poligon este mp */
sxmin = sxmax = P[n].v[X];
symin = symax = P[n].v[Y];
ms = n;
for (i = 1; i < s; i++)
else
if (P[n+i].v[Y] == symax && (P[n+i].v[X] > P[ms].v[X]))
ms = i;
else
if (P[n+i].v[Y] < symin)
symin = P[n+i].v[Y];
}
/*Indicele punctului de sus dreapta din al doilea poligon este ms */
/* Calculam punctul de start:cel de sus dreapta al ambelor poligoane*/
AddVec( p0, P[mp].v, p0 );
AddVec( p0, P[ms].v, p0 );
/* p0(X,Y) este punctul final de unde se incepe */
return mp; /* indicele de start. */
void SubVec(tPointi a,tPointi b,tPointi c )
void Vectorizare( void )
int Compara( const void *tpi, const void *tpj );
pi = (tPoint)tpi;
pj = (tPoint)tpj;
/* Un vector din semiplanul superior deschis este dupa un vector din semiplanul inferior inchis. */
if (( pi->v[Y] > 0) && (pj->v[Y] <= 0))
return 1;
else
if ((pi->v[Y] <= 0) && (pj->v[Y] > 0))
return -1;
/*Ambii vectori se afla pe axa x. */
else
if (( pi->v[Y] == 0) && (pj->v[Y] == 0))
/*Altfel, ambii se afla in semiplanul superior deschis,sau ambii se afla in semiplanul inferior inchis,dar nu ambii pe axa x*/
else
void Afisare(void)
void Marire_poligon(int j0,tPointi p)
i = (i+1)%m;
}
/* Avansam cu o latura din primul poligon. */
AddVec( p, P[i].v, p );
lineto(p[X],p[Y]);
getch();
j = (j+1)%n;
} while (j!=j0);
/* In final completam circuitul robotului(celui de-al doilea poligon)*/
while (i!=0)
i = (i+1)%m;
}
void main();
int j0; /* indicele punctului de start */
j0 = citire(p0);
initgraph(&gd,&gm,'c:bc31bgi');
errorcode = graphresult();
if (errorcode != grOk)
setlinestyle(SOLID_LINE,1,3);
setcolor(4);
Afisare();
Vectorizare();
qsort(&P[0],m,sizeof(tsPoint),Compara);
/* unde: - &P[0] este pointer la primul element
- m este numarul de elemente
- sizeof(tsPoint) este marimea fiecarui element
- compara este functie de comparare a elementelor */
setcolor(10);
Marire_poligon(j0,p0);
getch();
8:(50,50),(150,160),(250,60),(300,100), 4:(0,0),(20,0),(20,20),(0,20)
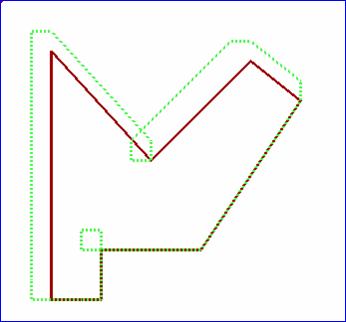
(200,250),(100,250),(100,300),(50,300)
12: (40,160), (160,120), (200,40), (240,80), (280,40), (320,120), (440,160), (320,200), (280,280), (240,240), (200,280), (160,200)
4: (0,0), (20,0), (20,20), (0,20).