Pozitii relative ale dreptei fata de plan

Pozitii relative ale dreptei fata de plan

In raport cu un plan o dreapta se poate gasi in una dintre urmatoarele pozitii relative: a) paralelism;  b) concurenta. Perpendicularitatea unei drepte fata de un plan este un caz particular al concurentei (intersectiei) dintre o dreapta si un plan (unghiul dintre dreapta si plan fiind de 90

a) Dreapta paralela cu planul

Fiind dat un plan oarecare si un punct exterior lui, se cere sa se construiasca prin punct o dreapta paralela cu planul. Rezolvarea se bazeaza pe teorema cunoscuta din geometria in spatiu:

Observatie: pentru ca intr-un plan se pot construi / alege o infinitate de drepte, rezulta ca se poate construi o infinitate de drepte paralele cu planul dat, ceea ce inseamna ca formularea problemei permite o infinitate de solutii. Pentru a obtine o solutie unica este nevoie si de o a doua conditie care sa precizeze directia dreptei ce indeplineste conditia de perpendicularitate.

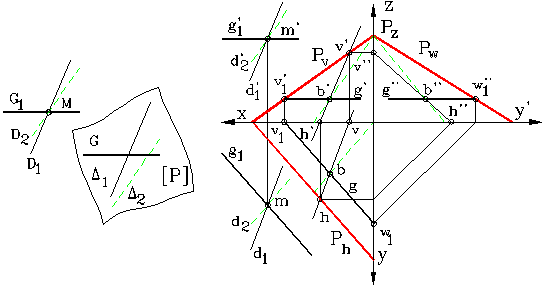
Fig. 14

In figura 14 este prezentata o schema intuitiva si constructia grafica a unei drepte paralele cu un plan determinat prin urmele sale. Asa cum s-a aratat anterior, printr-un punct exterior unui plan se pot construi o infinitate de drepte paralele cu planul dat, fiecare din ele fiind paralela cu o dreapta continuta in plan. Astfel, daca in planul [P] se aleg dreptele (D₁) si (D₂), prin [P] se pot construi doua drepte (D₁) D₁) si (D₂) D₂) care astfel sunt paralele cu [P].

Problema construirii unei drepte paralele la un plan are solutie unica doar daca se impune o con-ditie suplimentara (directia dreptei in spatiu, apartenenta ei la un alt plan etc.). In figura 14 este exem-plificata constructia prin a unei drepte (G₁) care: a) este paralela cu [P] si b) este o orizontala, adica (G₁) [H].

Pentru a fi paralela cu [P], (G₁) trebuie sa fie paralela cu o dreapta din [P] iar pentru a fi orizontala, trebuie ca insasi dreapta din plan sa fie orizontala.

Prin [P] s-a construit dreapta (G). Ea este o orizontala pentru ca :

1) proiectia verticala (g') a fost construita prin paralela cu axa (OX): (g') (OX);

2) proiectia laterala (g'') a fost construita prin paralela cu axa (OY'): (g'') (OY');

3) proiectia orizontala (g) a fost construita prin paralela cu urma orizontala a planului: (g) (P_h);

Dreapta (G) astfel construita este o dreapta continuta in planul [P] deoarece:

1) contine punctul B, B (G) iar acesta apartine planului;

2) urma sa verticala V₁ (v₁, v₁' ) are proiectia verticala v₁' situata pe urma verticala a planului, (P_V), ceea ce inseamna ca V₁ apartine planului [P]. Astfel (G) are doua puncte ce apartin planului [P] deci este continuta in acesta.

Prin urmare dreapta (G₁) construita prinparalela cu (G) este paralela cu [P].

De asemenea este paralela cu [P] dreapta (D₂) construita prinparalela cu dreapta (VH) din plan.

b) Dreapta concurenta cu planul

O dreapta intersecteaza un plan daca are doar un punct comun cu planul respectiv. Gasirea acestui punct comun este foarte usoara in cazul intersectiei dreptelor cu planele simplu si dublu particulare datorita proprietatilor acestora. Problema intersectiei dintre o dreapta si un plan oarecare se poate rezolva fie direct, fie transformand planul oarecare intr-un plan simplu particular. Ambele rezolvari presupun notiuni suplimentare.

1) Intersectia dintre o dreapta si un plan simplu particular

Fie planul vertical ([Q] [H]) definit prin punctele Q_X (40, 0, 0), Q_Y (0, 40, 0) si segmentul . Din figurile 15 si 16 se observa ca punctul D(20, 20, 20) este punctul de intersectie dintre planul [Q] si segmentul deoarece el apartine atat segmentului cat si planului.

Determinarea grafica, in epura, a punctului de intersectie se bazeaza pe rationamentul de mai jos.

1) Deoarece [Q] [H], punctele cuprinse in plan au proiectiile orizontale situate pe (Q_h), urma sa orizontala.

2) Un punct de intersectie dintre segmentul de dreapta si plan este cel a carui proiectie orizontala apartine concomitent proiectiei orizontale a segmentului si urmei orizontale a planului. Aceasta conditie o inde-plineste doar punctul notat d care rezulta din intersectia (ab) si (Q _h), adica d (ab) ∩ (Q _h).

3) Deoarece punctul de intersectie dintre plan si segmentul de dreapta este un punct al segmentului, el va avea proiectia verticala d' situata pe proiectia verticala a segmentului (a'b') iar proiectia laterala d'' apartine proiectiei laterale a segmentului (a''b'').

Fig. 15 Fig. 16

2) Intersectia dintre o dreapta si un plan dublu particular

In figurile 17 si 18 este prezentata determinarea punctului de intersectie dintre planul de nivel [N] avand cota z_[N] = 20 mm si segmentul . Rationamentul este asemanator cu cel prezentat anterior.

1) Deoarece [N] [H], atunci toate punctele cuprinse in plan au proiectiile verticale situate pe urma verticala (N _V ) a planului iar proiectiile laterale apartin urmei laterale a planului, (N _W).

2) Un punct comun al segmentului de dreapta si al planului este cel a carui proiectie verticala apartine concomitent proiectiei verticale a segmentului si urmei verticale a planului. Aceasta conditie o indeplineste doar punctul notat q' care rezulta din intersectia (m'p') si (N _V ), adica: q' (m'p') ∩ (N _V ).

3) Deoarece punctul de intersectie dintre plan si segmentul de dreapta este punct al dreptei, el satisface conditiile: proiectia orizontala q apartine proiectiei orizontale a segmentului (mp) si proiectia laterala q'' apartine proiectiei laterale a segmentului (m''p'').

Fig. 17               Fig. 18

i