
|
|
|
FORMULE DE CALCUL PRESCURTAT
(a+b)2=a2+2ab+b2 ; (a-b)2=a2-2ab+b2 ; a2-b2=(a+b)(a-b) ; (a+b+c)2=a2+b2+c2+2ab+2ac+2bc ;
(a+b)3=a3+3a2b+3ab2+b3 ; (a-b)3=a3-3a2b+3ab2-b3 ;
a3+b3=(a+b)(a2-ab+b2) ; a3-b3=(a-b)(a2+ab+b2) ;
PROPRIETATILE PUTERILOR
an∙am=an+m ; an:am=an -m ; (an)m=an∙m;(a∙b)n=an∙bn ; (a:b)n=an:bn ; a0=1; 0n=0 ; 1n=1
PROPRIETATILE RADICALILOR
![]() ;
; ![]() ;
;![]() ;
;![]() ; a≥0 ;
b≥0 ; y≥0 ; exemple:
; a≥0 ;
b≥0 ; y≥0 ; exemple:
![]() ;
;![]() ;
;![]() ;
; ![]() .
.
MODULUL
Definitie : |X|=X daca X≥0si|X|= -X daca X≤0 ;
Proprietati : |X|≥0; |a∙b|=|a|∙|b| ; |a+b|≤|a|+|b|
Exemple : |-5|= -(-5)=5;|7|=7;|-2|= -(-2)=2;|+4|=4;
FUNCTIA LINIARAf :R R , f(x)=ax+b
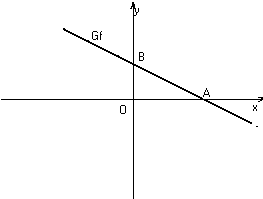 P(x,y)
P(x,y)![]() Gf daca si
numai daca f(x)=y ;
Gf daca si
numai daca f(x)=y ;
A(x,y)![]() Gf∩oxdacaf(x)=y si y=0 ;
Gf∩oxdacaf(x)=y si y=0 ;
B(x,y)![]() Gf∩oydacaf(x)=y si x=0 ;
Gf∩oydacaf(x)=y si x=0 ;
Daca f si g sunt doua functii atunci Q(x,y)![]() Gf∩Ggdacaf(x)=g(x)=y ;
Gf∩Ggdacaf(x)=g(x)=y ;
A(-b/a , 0)siB(0 , b)
MULTIMI DE NUMERE
Multimea numerelor naturale notata cu N : 0,1,2,3,4,.∞
Multimea numerelor intregi notata cu Z : -∞ . ,-4,-3,-2,-1,0,1,2,3,4,.+∞
Multimea numerelor rationale notata cu Q: exemple -3/4 ;5/2 ;-12/4 ;0,23 ;-5,(24) ;4,20(576) ;
Multimea numerelor reale notata cu R ; exemple : -3/4 ;5/2 ;-1/4 ;![]() ; -5,(24) ;4,20(576) ; 0,202002000200. ;-5,2323323332333323. ;
; -5,(24) ;4,20(576) ; 0,202002000200. ;-5,2323323332333323. ;
Orice numar natural este numar intreg : N![]() Z.
Z.
Orice numar intreg este numar rational :Z![]() Q.
Q.
Orice numar rational este numar real :Q![]() R.
R.
Avem urmatoarele relatii de incluziune intre
aceste multimi : N![]() Z
Z![]() Q
Q![]() R.
R.
Numerele reale care nu sunt numere rationale se numesc numere irationale.
FIGURI PLANE REMARCABILE
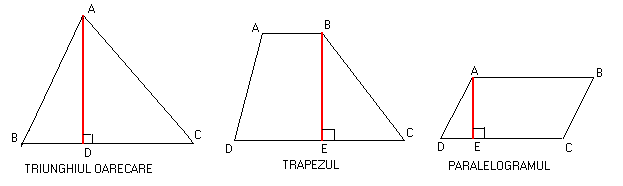 AΔABC=
AΔABC=![]() AABCD=
AABCD=![]() AABCD=
CD∙AE
AABCD=
CD∙AE
PΔABC= AB+BC+CAPABCD= AB+BC+CD+DAPABCD= 2∙(AB+BC)

AABCD=
AB∙BC AABCD=![]()
AC2=AB2+BC2
PABCD= 2∙(AB+BC)PABCD= 4∙AB
poligoane regulate : l=latura poligonului ; a=apotema poligonului ; A=aria ; P=perimetrul ;
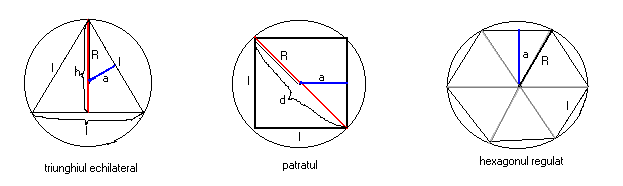 P=3∙l P=4∙lP=6∙l
P=3∙l P=4∙lP=6∙l
![]()
![]()
![]()
l=R![]() l=R
l=R![]() l=R
l=R
![]() d=l
d=l![]() =2R
=2R
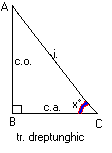
TRIUNGHIUL DREPTUNGHIC
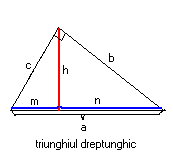 Teorema catetei: b2=a∙n ;c2=a∙m
Teorema catetei: b2=a∙n ;c2=a∙m
Teorema inaltimii: h2=m∙n ; ![]()
Teorema lui Pitagora:a2=b2+c2 ; c2=h2+m2si b2=h2+n2
Aria tr. dreptunghic: ![]()
FUNCTII TRIGONOMETRICE
|
functia |
30° |
60° |
45° |
functia |
30° |
60° |
45° |
|
sin |
|
|
|
tg |
|
|
1 |
|
cos |
|
|
|
ctg |
|
|
1 |
sin
x°=![]() cos x°=
cos x°=![]() tg x°=
tg x°=![]() ctg x°=
ctg x°=![]()
NOTATII UTILIZATE IN GEOMETRIA CORPURILOR REGULATE
Al -aria laterala ; At -aria totala ; V- volumul ; ap-apotema piramidei ; atr-apotema trunchiului
Ab-aria bazei mici ; AB-aria bazei mari ; Pb-perimetrul bazei mici ; PB-perimetrul bazei mari ;
h-inaltimea corpului ; m-muchia laterala ; ab-apotema bazei mici ; aB-apotema bazei mari ; l-latura bazei mici ; L-latura bazei mari ; g-generatoarea (la cilindru ,con ,trunchi de con);r-raza bazei mici ; R-raza bazei mari .
PRISMA , PIRAMIDA , TRUNCHIUL DE PIRAMIDA
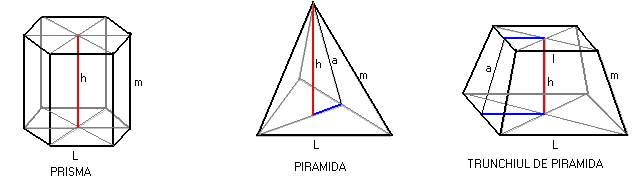
Al=PB∙mAl=![]() Al=
Al=![]()
At=Al+2∙AB At=Al+AB At=Al+Ab+AB
V=AB∙h V=![]() V=
V=![]()
CILINDRUL ,CONUL ,TRUNCHIUL DE CON
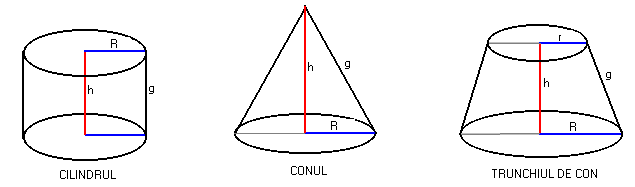
A=![]() Al=
Al= ![]() Al=
Al=![]()
At=![]() At=
At=![]() At=
At=![]()
V=![]() V=
V=![]() V=
V=![]()
SFERA ,CALOTA SFERICA ,PARALELIPIPEDUL DREPTUNGHIC
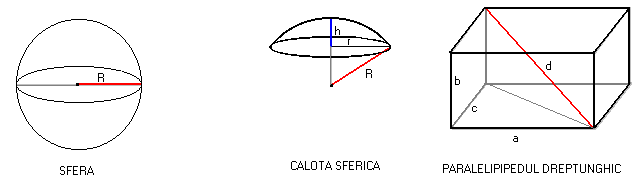
As=![]() Ac=
Ac=![]() At=
At=![]()
Vs=![]() R2=r2+(R-h)2
V= a∙b∙c
R2=r2+(R-h)2
V= a∙b∙c
![]()
TRIUNGHIURI ASEMENEA ,TEOREMA LUI THALES
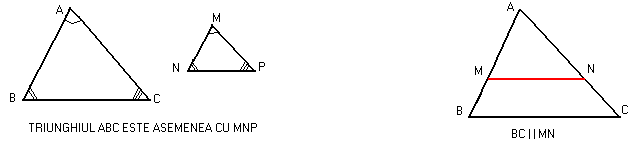
rezulta: ![]() rezulta:
rezulta: ![]()
CERCUL
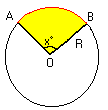 Dacam
Dacam![]() atunci :
atunci :
Lc=![]() ; LAB=
; LAB=![]()
Ac=![]() ;AOAB=
;AOAB=![]()