Scoruri standard (z)

Scoruri standard (z)

In psihologie, atunci cand masuram o anumita caracteristica a unui individ (timp de reactie, anxietate, nivel de performanta, etc.) scopul implicit este acela de a efectua comparatii. Pentru aceasta insa, simpla expresie numerica a caracteristicii respective nu este suficienta. Sa presupunem ca efectuam interviuri intr-o comisie de angajare si intrebam un candidat daca stie limba engleza. El ne raspunde "am sustinut, de curand, un examen de limba engleza la care am obtinut 70 de puncte". Daca examenul si modul de evaluare ne sunt total necunoscute, informatia nu ne spune mare lucru. Desigur, bazandu-ne pe experienta anterioara, putem face niste presupuneri dar acestea nu tin loc de certitudini.

Pentru a ne lamuri, ar trebui sa punem cateva intrebari suplimentare: Care este maximum si minimum de puncte posibil la acel examen? (daca maximul este 100 iar minimul este 0 atunci putem spune ca 70 este un scor este mai aproape de 100 decat de 0); Care este rezultatul mediu obtinut la acel examen? (daca raspunsul ar fi 60, inseamna ca 70 este o valoare peste medie cu 10 unitati); In fine, daca am dori sa apreciem cu maxima precizie semnificatia cifrei 70, ar trebui sa stim care este "imprastierea" rezultatelor obtinute de participantii la examen. Figura de mai jos plaseaza valoarea comunicata de candidatul nostru (70) in doua distributii ipotetice, avand, ambele, media 60 dar abateri standard diferite, sa spunem 5, respectiv 20.

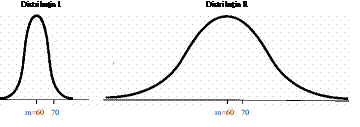
Daca privim cele doua distributii putem face doua observatii:

1. Pentru ambele distributii, valoarea 70 este cu 10 unitati peste medie (60)
2. In cazul distributiei I, mai omogena, scorul 70 se plaseaza catre extrema valorilor, in timp ce, in contextul distributiei II, cu imprastiere mai mare, este mai aproape de medie decat de valorile superioare.

Modalitatea de a exprima semnificatia unei anumite valori dintr-o distributie prin raportare la parametrii distributiei (medie si abatere standard) este scorul normat z (numit si nota z sau scor z). Aceasta masoara distanta dintre o anumita valoare si media distributiei, in abateri standard:

unde X reprezinta oricare dintre valorile distributiei

Pentru cele doua distributii de mai sus, scorurile z se calculeaza astfel:

respectiv,

Iar in cazul in care pentru distributia II am avea un scor de 45:

Semnul "-" ne arata ca performanta este mai mica decat media si se afla la 0.75 abateri standard de medie. Semnul "+" indica o valoare standardizata peste medie, indicand, in exemplul de mai sus, ca se plaseaza la o jumatate de abatere standard deasupra mediei.

Scorul z se numeste si "scor standardizat" (nota standardizata). Aceasta pentru ca poate fi utilizata pentru a compara valori care provin din distributii diferite, indiferent de unitatea de masura a fiecareia.

Exemplu: Daca un subiect obtine un scor echivalent cu z=+0.2 la un test de calcul aritmetic si un scor echivalent cu z=+0.1, la un test de reprezentare spatiala, se poate spune ca are o performanta mai buna la primul test decat la al doilea.

Calcularea valorii atunci cand cunoastem parametrii notei z

Daca calculam scorurile (notele) z pentru fiecare dintre valorile unei distributii, am realizat o "distributie in note z" a acelei distributii. In tabelul urmator, distributia X a fost transformata in distributie z.

Utilizand proprietatile de transformare a formulei de definitie a scorului z, putem calcula o anumita valoare atunci cand cunoastem valoarea lui z si parametrii distributiei, astfel:

Daca

atunci: X=z*s+m adica, pentru ultimul exemplu: X=-0,75*2.38+12.8=11

Proprietatile scorurilor z

1. Media unei distributii z este intotdeauna egala cu 0. Aceasta rezulta din proprietatea mediei de a se diminua corespunzator daca se extrage o constanta din fiecare valoare a unei distributii. Formula de calcul pentru z implica scaderea unei constante din fiecare valoare a distributiei. Aceasta inseamna ca si media noii distributii (z) se va reduce cu constanta respectiva. Dar aceasta constanta este insasi media distributiei originale, ceea ce inseamna ca distributia z va avea media egala cu zero, ca rezultat al diminuarii mediei cu ea insasi.

2. Abaterea standard a unei distributii z este intotdeauna 1. Acest fapt decurge prin efectul cumulat al proprietatilor abaterii standard. Prima proprietate afirma ca in cazul scaderii unei constante (in cazul scorurilor z, media) din valorile unei distributii, abaterea standard a acesteia nu se modifica. A doua proprietate afirma ca in cazul impartirii valorilor unei distributii la o constanta, noua abatere standard este rezultatul raportului dintre vechea abatere standard si constanta. Dar constanta de care vorbim este, in cazul distributiei z, chiar abaterea standard. Ca urmare, noua abatere standard este un raport dintre doua valori identice al carui rezultat, evident, este 1.

Alte tipuri de scoruri standardizate

Notele z prezinta doua avantaje importante: permit compararea valorilor unei distributii, si a valorilor provenind din distributii diferite, ca urmare a faptului ca se exprima in abateri standard de la medie. Totusi se impune o anumita precautie in comparatia pe baza scorurilor z atunci cand distributiile au forme diferite si, mai ales, asimetrii opuse.

Notele z au, insa, si unele dezavantaje: se exprima prin numere mici, cu zecimale, (greu de manipulat intuitiv) si, in plus, pot lua valori negative. Aceste dezavantaje pot fi usor inlaturate printr-un artificiu de calcul care sa conduca la note standardizate convenabile (ce corespund anumitor nevoi specifice). In tabelul de mai jos sunt descrise cateva tipuri de note standard calculate pe baza notelor z.

Observatii:

1.     Toate variantele sunt obtinute prin transformarea operata pe distributia de note z.

2.     La nici una dintre variante nu mai avem valori negative (cu conditia ca distributia sa nu aiba o variabilitatea aberanta).

3.     Zecimalele nu mai sunt semnificative (ele rezulta din calcule, dar sunt ignorate).

4.     Distributiile variantelor oscileaza in jurul unei valori medii specifice, sub care se afla 50% din valori, si peste care se afla restul de 50% dintre valori.

5.     Notele standard mari indica o valori mari iar notele standard mici indica valori mici. Acest fapt poate crea dificultati in unele cazuri. Sa luam urmatorul exemplu: Un subiect realizeaza 145 raspunsuri corecte la un test de calcul aritmetic (m=120, s=12) si un timp de reactie de 0.15 sec., la un test de reactivitate (m=0,11, s=0,05). In acest caz, notele T corespunzatoare celor doua performante sunt: T₁=50+10*(145-120)/12=70, respectiv T₂=50+10*(0,15-0,11)/0,05=58. Cu alte cuvinte, ar rezulta ca la ambele teste subiectul nostru a obtinut un rezultat peste medie. Dar aceasta concluzie este falsa, daca tinem cont ca la testul de reactivitate un timp mai mare inseamna o performanta mai scazuta. Solutia problemei consta in modificarea semnului expresiei de calcul, in functie de semnificatia calitativa a valorilor distributiei. In acest mod, rezultatul transformarii in nota standard la testul de reactivitate devine: T₂=50-10*(0,15-0,11)/0,05=42, ceea ce indica exact semnificatia de performanta sub medie. Raportata la valoarea medie a distributiei T, scorul 58 este echivalent cu 42, sub aspectul distantei fata de medie (8 unitati). Diferenta consta in faptul ca valoarea 42 exprima si in mod intuitiv, nu doar cantitativ, evolutia performantei la test. O asemenea transformare nu este obligatorie, se poate utiliza oricare dintre formule, cu semnul plus, sau minus. In orice caz, trebuie sa precizam semnificatia valorilor mari si mici pentru distributiile cu care operam.

Nota 1: Scorurile Thurstone sunt cunoscute mai ales datorita utilizarii lor in evaluarea scalelor chestionarului MMPI, unul dintre cele mai celebre teste de personalitate.