Modelul sistemic al reglarii optimale a serviciului public

Modelul sistemic al reglarii optimale a serviciului public

Serviciile publice pot fi modelate ca niste sisteme dinamice complexe, cu o arhitectura mixta care include si o a treia bucla feed-back, datorata politicilor publice. Totodata, perspectiva abordarii sistemice a serviciilor publice ne conduce la considerarea acestora ca subsisteme ale administratiei publice ale caror obiective, cuantificate in iesirile sistemului, se definesc in raport cu satisfacerea unor nevoi sociale, nevoi determinate pe baza interesului public. Multe dintre servicii publice au caracter administrativ, datorat faptului ca acestea sunt organizate de colectivitatile publice teritoriale dupa regulile obisnuite ale administratiei publice.

Caracterul propriu-zis administrativ se atenueaza in cadrul serviciilor publice care actioneaza in domeniul economic, situatie in care se cauta sa se apropie, pe cat posibil, de procedeele de gestiune ale institutiilor private.

Incercari privind modelarea sistemica a serviciilor publice au mai fost prezentate in literatura romaneasca si au la baza urmatoarele caracteristici:

utilizeaza modelarea probabilistica a faptelor administrativ-sociale sau
economice specifice functionarii serviciilor publice;

sunt definitesievidentiatecaracteristicile ciberneticealesistemului
serviciului public;

realizeaza fundamentarea sistemica a deciziei publice in cadrul serviciului
public, oferind criteriile si metodele de optimizare a acestora;

utilizeaza si modelari care vizeaza nivelurile de aspiratie ale consuma-
torilor la a caror determinare sunt utilizate metode specifice stiintelor
conexe teoriei generale a sistemelor.

Ideea generala dupa care se realizeaza modelarea si optimizarea deciziei publice face apel la teorii cunoscute in matematicile economice referitoare la modelele de asteptare .

a)    In esenta, orice sistem al unui serviciu public este un sistem de asteptare in care fiecare consumator beneficiaza de serviciul solicitat dupa anumite reguli si intr-o anumita ordine.

1 Echilibrul dinamic

Cea mai mare parte a sistemelor de asteptare se caracterizeaza printr-o mare variabilitate a ratei intrarilor in sistem si a realizarii serviciului public pentru consumator.

Ca urmare, reglarea, in vederea obtinerii echilibrului, in cadrul unui sistem al serviciului public realizeaza o optimizare a raportului cerere - oferta pentru serviciul public respectiv.

Avand in vedere variabilitatea cererilor, sub raport cantitativ si calitativ, reglarea in cadrul serviciilor publice impune studierea unor fenomene si interactiuni sociale, ce se inscriu in sfera economiei publice, cunoscute sub denumirea de fenomene de asteptare. Modelul acestor fenomene poate fi reprezentat logic printr-un fir de asteptare si poate fi semnalat ori de cate ori ,,cererea de servicii depaseste capacitatea curenta de a asigura serviciile cerute.Aparitia firelor de asteptare are, uneori, si o determinare temporala, datorata variabilitatii cererii si care, pentru anumite perioade de timp, supraincarca sistemul, iar, pentru alte perioade, il subincarca.

Feed-back-ul activitatilor in cadrul unui serviciu public, in conditiile acceptarii variabilitatii cererii, trebuie sa ofere informatii pentru luarea deciziilor optime asupra capacitatii serviciului public.

Desi sunt aspecte specifice pentru serviciile publice care influenteaza costurile serviciului respectiv in modelul prezentat, aspectele topologice ale serviciului public nu vor fi luate in considerare.

Elementele de baza ale modelului sistemic al serviciului public vor fi:

• Intrarile reprezentate de consumatorii potentiali. Caracteristica acestui element este marimea, care poate fi finita sau infinita. Pentru serviciile publice marimea intrarilor poate fi considerata infinita, chiar daca, in realitate, este finita, dar suficient de mare. In legatura cu acestea vom face urmatoarele ipoteze :

Probabilitatea de intrare in sistem a unui potential consumator, la un moment dat, este constanta si nu depinde de ceea ce s-a intamplat anterior;

Probabilitatea de intrare intr-un interval foarte mic de timp, (t, t + h), este proportionala cu lungimea, h, a intervalului considerat, deci va fi egala cu:

λh + o(h),λ= const.>0                       (1.1)

unde, o (h) este o functie cu proprietatile:

(1.2)

- Probabilitatea ca in intervalul de timp (t, t + h) sa existe mai mult decat o intrare in sistem este aproape nula, adica egala ol(h) care indeplineste conditiile (1.2).

In aceste conditii, intrarile in sistem vor fi modelate de o variabila aleatoare X a carei lege de repartitie este chiar repartitia Poisson . Ca urmare, probabilitatea ca in intervalul de timp (o, t), t > o sa aiba loc n intrari in sistem va fi:

                         (1.3)

deci in unitatea de timp(t=1) avem:

                      (1.4)

Iesirile sunt reprezentate de persoanele care au beneficiat de serviciul solicitat. Si pentru iesiri pot fi formulate ipoteze asemanatoare ca pentru intrari. Prin urmare, iesirile vor fi modelate printr-o variabila aleatoare, Y, care are legea de repartitie, legea Poisson, cu parametrul µ.

Un rezultat cunoscut in literatura de specialitate se refera la faptul ca, daca T este variabila aleatoare care reprezinta timpul scurs intre doua intrari succesive, atunci T este o variabila aleatoare continua a carei lege de repartitie este de tip exponential, cu parametrul X. Prin urmare, densitatea de repartitie a lui T va fi:

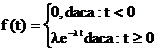                 (1.5)

iar functia de repartitie va fi :

                               (1.6)

a carei medie va fi:

                            (1.7)

iar dispersia

                         (1.8)

Analog, variabila aleatoare, U, reprezentand timpul scurs intre doui iesiri consecutive, va avea o repartitie exponentiala cu parametrul µ.

.Ecuatiile de stare vor modela o succesiune de stari: E_o, Ei, , E_n, care

constituie traiectoria sistemului.

Fiecarei stari ii asociem probabilitatea P_n (t) care va fi reprezentata de o functie continua si derivabila si care verifica:

                          (1.9)

determinarea probabilitatilor P_n(t), nN este esentiala pentru estimarea comportamentelor si parametrilor de performanta ai sistemului.

Pentru aceasta vom deduce un sistem de ecuatii numit sistemul ecuatiilor de stare. Daca presupunem cunoscute :

Probabilitatea de trecere de la starea E_n la starea E_n+1, in intervalul (t, t+h) este :

                    (1.11)

si corespunde unei noi intrari in sistem:

Ca urmare probabilitatea de a ramane in starea E_n, deci de a nu a avea nici o intrare, va fi :

           (1.12)

Probabilitatea de trecere de la starea E_n la starea E_n-1, in intervalul de timp (t, t+h), este :

                    (1.13)

si corespunde unei iesiri din sistem. Probabilitatea de a ramane in starea E_n, deci de a nu avea nici o iesire, va fi :

           (1.14)

Probabilitatea de trecere din starea E_n intr-o stare E_n-k sau E_n+k, kN, k >1 este o(h). Deci, intr-un interval foarte scurt de timp, pot avea loc cel mult o intrare si cel mult o iesire, atunci ecuatiile de stare ale sistemului serviciului public vor fi :

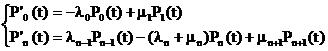      (1.15)

care reprezinta un sistem liniar infinit de ecuatii diferentiate rezolvabil in conditiile initiale.

Un caz particular, mai simplu de rezolvat, il reprezinta cadrul stationar, cand probabilitatile sunt constante.

In acest caz din 15 obtinem:

            (1.16)

si utilizand 9

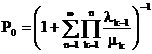                               (1.17)

presupunand ca, pentru orice stare a sistemului, rata medie a intrarilor este egala cu rata medie a iesirilor, ecuatia care exprima acest principiu va fi ecuatia de echolibru a starii n. Astfel pentru n=0, ecuatia de echilibru va fi:

                 (1.18)

iar pentru n≠0, ecuatia de echilibru va fi:

                     (1.19)

Performantele serviciului public sunt masurate utilizand diversi indicatori si reprezinta gradul maxim de satisfactie ce poate fi oferit consumatorului, precum si gradul de utilizare a capacitatii serviciului public.

Acesta vor avea in vedere timpul de asteptare, ordinea de servire, intensitatea de trafic sau factorul de utilizare a capacitatii de servire. Pentru cuantificarea acestora vom introduce noi relatii de baza, exprimate prin variabile aleatoare, discrete sau continue si caracteristici ale acestora.

Astfel, vom considera ca un consumator se afla in sistem din momentul in care acesta a solicitat un serviciu pana in momentul in care poate beneficia de acesta.

1.    In acest context, daca n este variabila aleatoare numar de clienti aflati in sistem repartitia acestuia va fi:

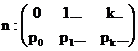(8.31.20)

a carei valoare medie

                                (1.21)

daca n_f = variabile aleatoare numarul de clienti aflati in firul de asteptare, atunci:

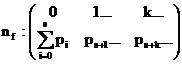  (1.22)

iar valoarea medie:

                    (1.23)

s reprezentand numarul de puncte(statii) in care un potential consumator poate beneficia de serviciul dorit.

O alta marime ce poate fi introdusa o repezinta numarul clientilor in curs de servire, care va fi reprezentata tot de o variabila discreta, n_s, cu repartitia:

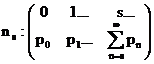          (1.24)

si valoarea medie:

(1.25)

evident ca:

si (1.26)

                                (1.27)

In mod analog, variabila aleatoare L, numarul de statii libere, va fi definita astfel:

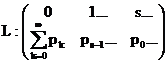     (1.28)

cu valoare medie:

                             (1.29)

observam ca:

                                  (1.30)

Se mai poate introduce variabila aleatoare t, reprezentand timpul de asteptare al unui client in sistem pentru care s-a demonstrat ca valoarea medie este:

                                       (1.31)

relatia reprezinta relatia lui Little.

O alta masura a performantei sistemului este factorul de serviciu sau intensitatea de trafic, definit astfel:

                                          (1.32)

precum si factorul de utilizare a capacitatii serviciului public:

                                        (8.31.33)

care reprezinta procentul de timp cat serviciul public functioneaza la capacitate maxima.

Literatura de specialitate releva mai multe tipuri de modele adaptabile sistemelor serviciilor publice. Cel mai relevant dintre acestea este modelul sistemic cu s statii de servire identice si populatie infinita. In aceste conditii:

si                        (1.34)

       (1.35)

iar

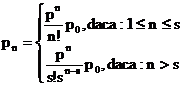(1.36)

de unde:    (8.31.37)

va rezulta si expresia lui p₀, tinand seama de()

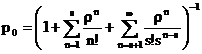                              (1.38)

care in conditiile ρ^* <1, va fi:

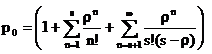                           (1.39)

care in conditiile ρ^*≥1, atunci serviciul public se supraaglomereaza si, teoretic, nu mai poate fi analizat dupa modelul prezentat in aceasta abordare.

Obtinem de asemenea:

             (3.2.1.40)

Interesante pentru determinarea feed-back-ului si traducerea acestuia in informatii utile pentru determinarea performantelor serviciului public si eventuala reproiectare a sa sunt comparatiile diverselor marimi caracteristice obtinute cu unele valori de referinta. De exemplu, se poate calcula probabilitatea ca un posibil consumator sa astepte mai mult decat un interval de timp standard t₀:

                                  (1.41)

2 Optimizarea in serviciile publice

Din punctul de vedere al serviciului public, feed-back-ul fundamenteaza si determina. deciziile care privesc imbunatatirea performantelor sistemului existent sau proiectarea unui nou sistem cu parametrii doriti.

Astfel de parametri pot fi: rata de serviciu, µ, numarul statiilor de servire, s, numarul consumatorilor potentiali care au acces in sistem.

,,Optimizarea parametrilor poate fi privita din mai multe puncte de vedere, conform cu obiectivul decidentului. Un mod obisnuit de tratare este acela de a construi un model de decizie cu costuri care sa minimizeze suma costurilor asociate asteptarii si a costurilor asociate servirii, pe unitatea de timp. Cu cat primul cost este mai mare, cu atat al doilea este mai mic si reciproc. Modelele de optimizare cu costuri sunt foarte eficiente daca se pot deduce efectiv costurile unitare componente. Cand acest lucru este greu de facut si nici estimarile nu sunt suficient de bune, este obligatoriu sa se caute un alt criteriu de optimizare.

2.1 Etape ale optimizarii serviciilor publice utilizand costurile

In general, modelele utilizate pentru modelarea sistemica a serviciului public reprezinta instrumente de analiza utilizate in vederea cresterii performanttelor acestora.

In multe situatii putem introduce costuri si, astfel, sa oferim posibilitatea determinarii unui model de optimizare a activitatii in cadrul serviciului public menit sa ridice nivelul de satisfacere a preferintelor consumatorului.

Pentru operationalizarea unui astfel de model trebuie sa parcurgem urmatoarele etape:

definirea variabilelor in vederea descrierii problemei;

deducerea repartitiilor probabilistice asociate, bazate pe datele reale si utilizarea unor teste corespunzatoare;

construirea functiei cost asociate sistemului utilizand costurile de asteptare;

deducerea solutiei optime din model si testarea valabilitatii acesteia in practica.

In acest context vom considera ca c₁ reprezinta costul cresterii cu o unitate a ratei de serviciu, µ, pe unitatea de timp, iar c₂ costul asteptarilor pe unitatea de timp pentru client.

2.1.1 Criterii de optimizare utilizand costurile

a) Rata optima de servire determina intervalul optim in care poate fi servit un client.

Cu semnificatiile atribuite anterior variabilelor modelului, functia obiectiv ce urmeaza a fi minimizata va fi:

sau

        (2.1.1.1)

Utilizand tehnici simple de optimizare, in situatia in care λ < μ obtinem:

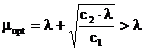       (2.1.1.2)

Aceasta expresie arata ca rata optima nu depinde numai de costurile c₁ si c₂, ci si de parametrul intrarilor in sistem.

b) Numarul optim de statii de servire presupune determinarea numarului de statii de servire astfel incat sa se utilizeze la maximum capacitatea serviciului public, iar timpul de servire sa fie minim. Astfel, daca c₁ reprezinta costul adaugarii unei statii, pe unitatea de timp, iar c₂ costul asteptarii pe unitatea de timp, pentru un client, s fiind variabila de decizie care semnifica numarul de statii de servire, atunci functia obiectiv va fi:

(2.1.1.3)

n (s) reprezentand numarul mediu de unitati in sistem, atunci cand acesta are exact s statii de servire.

Variabila s fiind o variabila discreta, metoda de optimizare va utiliza o metoda combinatorica bazata pe observatia ca numarul mediu de unitati in sistem, n (s), este o functie descrescatoare.

Presupunand ca s_opt reprezinta numarul optim de statii vor trebui indeplinite simultan conditiile:

                          (2.1.1.4)

adica folosind((3.2.2.1.1.3)):

    (8.32.1.1.5)

care devine echivalent cu:

    (2.1.1.6)

In concluzie, raportul indica numarul optim de statii de servire care ar trebui introduse astfel incat functia cost Γ(s) sa fie minima.

3 Modelul nivelurilor de aspiratie

In aceasta situatie optimalitatea este privita in sensul satisfacerii anumitor niveluri de aspiratie stabilite de decident. Aceste niveluri sunt definite ca limite snperioare stabilite pentru valorile masurilor conflictuale ale performantei sistemului, pe care autoritatea publica doreste sa-l echilibreze.Introducerea acestui model are in vedere dificultatea de a determina cu precizie costurile cerute in modelul de optimizare.

Din punctul de vedere al clientului, cele mai relevante marimi pentru determinarea performantei sistemului sunt:

t, timpul mediu de asteptare in sistem;

procentajul de statii care nu functioneaza, X.

Pentru fiecare dintre cele doua marimi, autoritatea publica, pe baza nivelurilor de aspiratie, stabileste limitele superioare α pentru t si β pentru X. Deci problema de optimizare se formuleaza astfel: sa se determine numarul de statii, s_opt, astfel incat:

                             (3.1.)

expresia lui este cunoscuta din (), iar X se defineste astfel:

                   (3.2)

Grafic, acest model se poate reprezenta pe un sistem de axe ca in figura urmatoare:

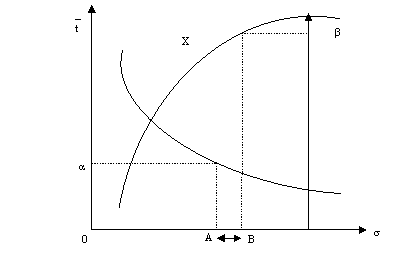
Fig. 3.1. Modelul nivelurilor de aspiratie

Observam ca in fig.3.1 Cele doua conditii (3.1) sunt simultan indeplinite. In caz contrar este necesar sa se relaxeze una sau amandoua din cele doua conditii pentru a determina s_opt. Modelul nivelurilor de aspiratie poate fi folosit si pentru deducerea costului, c₂, de asteptare a clientului pe unitatea de timp daca se cunosc: costul c₁, nivelurile de aspiratie α si β si numarul s al  statiilor de servire.

Astfel utilitand (2.1.1.6) vom avea:

                             (3.3)

relatia ce precizeaza un anumit interval pentru c₂, daca numarul de statii de servire este ales conform nivelelor de aspiratie α si β.