|
|
|
STATICA FLUIDELOR
1 LEGEA FUNDAMENTALA A STATICII FLUIDELOR
In cadrul staticii fluidelor se studiaza
proprietatile fluidelor aflate in stare de repaus. Un fluid se
considera in stare de repaus daca orice element de volum din
structura sa are la orice moment o viteza nula, adica are un
camp de viteze nul. Campul de presiune va fi in acest caz o functie de
punctul considerat, adica 
.
Daca fluidul este ideal si se afla in repaus, atunci intre diferitele sale straturi nu pot apare forte tangentiale de interactiune. Prezenta unor asemenea forte ar contribui la deplasari ale straturilor de fluid, si deci fluidul nu ar mai fi in repaus. Prin urmare, in cazul fluidelor ideale aflate in repaus singurele forte care apar sunt cele normale numite forte de presiune.
Problema fundamentala a staticii fluidelor o constituie obtinerea unei legi care sa permita determinarea campului de presiune in interiorul unui fluid aflat in repaus.
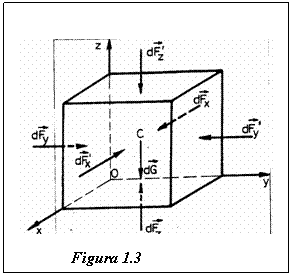
Sa consideram un element de volum infinitezimal in fluidul aflat in echilibru, de masa dm si avand forma unui paralelipiped cu laturile dx, dy, dz (fig.1.3.).
Vom presupune ca singura forta exterioara de volum care actioneaza asupra fluidului este determinata de campul gravitational. Ea are expresia:
(1.12)
unde 
reprezinta
vectorul acceleratiei gravitationale.
Deoarece:
(1.13)
si dV=dxdydz expresia (1.12) devine:
(1.14)
unde r(x,y,z) reprezinta densitatea fluidului in centrul C al elementului de volum dV.
Actiunea restului fluidului asupra acestui
element de volum poate fi inlocuita prin forte 
, normale pe fetele lui si indreptate spre
interiorul lui.
La echilibru, putem scrie de exemplu pentru fetele perpendiculare pe Ox:
(1.15)
decip = p'
unde p este presiunea pe fata elementului de volum continuta in planul yOz si p' presiunea pe fata paralela cu ea.
Un rezultat asemanator se obtine scriind conditia de echilibru pentru fetele perpendiculare pe axa Oy.
(1.16)
decip = p'
Valoarea presiunii este, deci, aceeasi pentru o valoare data a lui z, oriunde s-ar afla suprafata pe care ea se exercita, deci presiunea este aceeasi in toate punctele unui plan orizontal.
Sa scriem conditia de echilibru in cazul fetelor perpendiculare pe directia Oz:
(1.17)
(1.18)
(1.19)
unde dp=p1'-p1
Relatia (1.19.) se mai poate scrie sub forma:
(1.20)
Expresia (1.20.) reprezinta legea fundamentala a staticii fluidelor scrisa pentru cazul cand singurele forte exterioare de volum ce actioneaza asupra fluidului sunt cele determinate de campul gravitational.
Daca se admite ca asupra elementului de
fluid considerat actioneaza si alte forte exterioare de
volum si se noteaza prin 
valoarea rezultanta
a tuturor fortelor exterioare de volum, raportata la unitatea de
masa a fluidului, atunci legea fundamentala a staticii fluidelor se
va scrie sub forma generala:
(1.21)
1.2.2 PRESIUNEA HIDROSTATICA
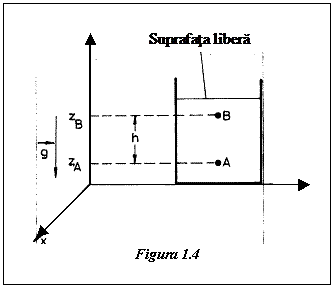
Sa determinam distributia presiunii intr-un fluid incompresibil (r=const.), de exemplu un lichid aflat in repaus in campul gravitational (fig.1.4.).
Legea fundamentala (1.20.)
poate fi inlocuita in acest caz prin urmatoarele trei ecuatii
scalare:
(1.22)
Gradientul presiunii care caracterizeaza variatia presiunii in spatiu si este dat de derivatele partiale ale acesteia, este un vector perpendicular pe suprafetele de presiune constanta (in sensul cresterii
presiunii), deci este perpendicular pe suprafetele de camp gravitational constant in sensul acestui camp. In cazul de mai sus aceste suprafete sunt orizontale si campul este vertical in jos, de aceea gradientul presiunii s-a redus numai la componenta verticala. Ultima ecuatie din (1.22) se poate scrie atunci sub forma:
(1.23)
Fluidul fiind presupus incompresibil (r=const), ecuatia (1.23.) poate fi integrata intre limitele ce corespund, de exemplu, punctelor A si B:
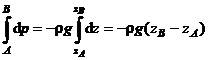sau
(1.24)
unde h este diferenta de nivel intre punctele B si A.
Expresia rgh este denumita presiune hidrostatica si reprezinta presiunea pe care o exercita in punctul A lichidul cuprins intre nivelele ce trec prin A si respectiv B.
Daca punctul B este chiar pe suprafata lichidului, atunci se noteaza pB cu p0, unde p0 reprezinta presiunea atmosferica. Considerand punctul A arbitrar ales ecuatia (1.24) devine:
(1.25)
unde h reprezinta adancimea la care se afla punctul in care se calculeaza presiunea p.
Daca campul de forte exterioare ce
actioneaza asupra fluidului este conservativ, atunci forta de
volum deriva dintr-un potential, in sensul ca poate fi
scrisa sub forma 
U. Raportand aceasta forta la unitatea de masa se
obtine:
U 
= - V (1.26)
unde V = U/m reprezinta potentialul campului exterior.
Din relatiile (1.21) si (1.26) rezulta:
p V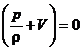 
, adica
(1.27)
Relatia (1.27) exprima faptul ca intr-un fluid incompresibil aflat in repaus intr-un camp exterior de forte conservative, suprafetele de presiune constanta sunt in acelasi timp si suprafete de potential constant, adica sunt suprafete echipotentiale.
In exemplul considerat suprafetele echipotentiale sunt plane orizontale.
Suprafata lichidului, numita suprafata libera, este de asemenea o suprafata echipotentiala. Pe aceasta proprietate se bazeaza principiul vaselor comunicante, conform caruia nivelul unui lichid turnat in doua vase ce comunica intre ele este acelasi in ambele vase.
3. FORMULA BAROMETRICA
O aplicatie a legii fundamentale a staticii fluidelor o constituie deter-minarea campului de presiune intr-un fluid compresibil aflat in echilibru in campul gravitational al Pamantului, de exemplu atmosfera. Fluidul se caracterizeaza prin proprietatea ca densitatea sa intr-un punct oarecare este functie numai de presiunea din acel punct: r r(p). Astfel de fluide se numesc barotrope. Exemple de astfel de fluide sunt gazele ideale, apa marilor si oceanelor, atmosfera Pamantului.
Legea fundamentala a staticii fluidelor se scrie pentru fluidele barotrope, astfel:
(1.28)
Prin integrare rezulta:
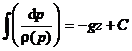(1.29)
unde C este o constanta de integrare ce se determina din conditii la limita.
Se alege o forma particulara pentru functia r(p) cu scopul de a evalua analitic sau numeric integrala din membrul stang al relatiei (1.29). Se considera ca fluid barotrop gazul ideal. Se utilizeaza ecuatia de stare a gazului ideal:
(1.30)
din care se poate exprima densitatea:
(1.31)
Inlocuind (1.31) in (1.29) si integrand rezulta:
(1.32)
Daca se admite conditia la limita p=p0
pentru z=0, rezulta 
.
Relatia (1.32) devine:
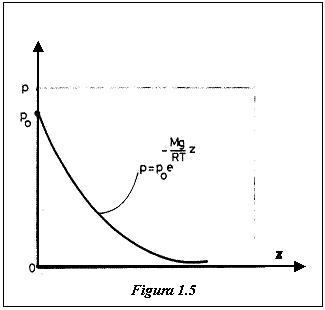
(1.33)
Relatia (1.33) constituie formula barometrica si arata ca in cazul fluidelor compresibile barotrope, aflate in camp extern gravitational si care se supun legii gazelor perfecte, presiunea scade exponential cu inaltimea (fig. 1.5.).
Cercetarile experimentale au pus in evidenta faptul ca atmosfera Pamantului poate fi considerata ca un fluid barotropic pentru care este valabila formula barometrica. Pentru ea, nivelul z=0 se alege nivelul marii.
