Principiul al doilea al termodinamicii. entropia

PRINCIPIUL AL DOILEA AL TERMODINAMICII. ENTROPIA

Am vazut in paragraful anterior ca primul principiu al termodinamicii generalizeaza conceptul de energie mecanica prin cel de energie totala, o marime conservativa ce caracterizeaza un sistem termodinamic. Lucrul mecanic si caldura au aparut ca forme ale schimbului de energie ce pot sa se transforme una in alta.

Totusi am remarcat o diferenta esentiala intre lucru mecanic si caldura: lucrul mecanic este un schimb de energie de natura macroscopica, iar caldura este de natura microscopica. Principiul al doilea al termodinamicii subliniaza aceasta diferenta.

Principiul al doilea al termodinamicii se bazeaza pe conceptul de entropie, ce permite sa se stabileasca sensul de evolutie al proceselor termodinamice reale.

Vom enunta principiul al doilea pentru sisteme inchise si vom ilustra aplicarea sa pe sisteme termodinamice simple.

1.                  Enuntul principiului al doilea al termodinamicii

Pentru orice sistem inchis, exista o functie extensiva, de variabilele de stare, neconservativa, numita entropie, a carei variatie, intre doua stari succesive t₁ si t₂ (t₂>t₁) se scrie:

(1.20)

S_p este entropia schimbata de sistem in cursul procesului, S_prod este productia de entropie, iar T o marime intensiva, pozitiva, numita temperatura termodinamica.

Este de remarcat ca S_p este direct legata de caldura schimbata prin suprafata S ce delimiteaza sistemul. Termenul de productie de entropie are acelasi semn pe intervalul t₁, t₂, deci acest termen este cel ce determina sensul de evolutie al sistemului, permite de a numi ireversibile procesele reale si furnizeaza o interpretare macroscopica conceptului de entropie.

Egalitatea S_prod=0 corespunde unor transformari reversibile. In acest unic caz S= S_p.

Temperatura termodinamica este introdusa aici fara explicatii suplimentare. Se poate arata ca aceasta poate fi identificata cu temperatura cinetica (absoluta) ce intervine in ecuatia de stare a gazului perfect.

Toate procesele termodinamice reale sunt procese ireversibile. Exista mai multe cauze pentru ireversibilitatea (producerea de entropie) proceselor termodinamice din care vom aminti doar cateva:

- frecarea  - lucrul mecanic produs de aceste forte se transforma in energie interna sau caldura;

- neuniformitatea marimilor intensive in sistemul considerat (presiune, temperatura, etc.);

Pentru a intelege calitativ notiunea de entropie, sa consideram un sistem izolat, pentru care S=S_prod. Un astfel de sistem evolueaza spontan spre starea de echilibru caracterizata de uniformitatea parametrilor. Boltzmann a exprimat aceasta evolutie in termeni de ordine: sistemul izolat evolueaza spre starea de dezordine maxima, iar entropia furnizeaza o masura a acestei dezordini.

2. Enunturi echivalente ale principiului al doilea

Exista trei enunturi ale principiului al doilea care au o importanta istorica: enuntul inginerului francez S. Carnot din 1824, cel al germanului R. Clausius din 1850 si cel al scotianului W. Thomson din 1852.

Enuntul lui S. Carnot

Carnot a formulat doua teoreme ce contin cel de-al doilea principiu al termodinamicii dar au deficienta de a avea un caracter specializat. In acest fel se restrange semnificatia acestui principiu foarte general la aspecte tehnice legate de functionarea masinilor termice:

Teorema 1

Randamentul unei masini biterme reversibile depinde numai de temperaturile izvorului cald T₁ si a izvorului rece T₂ si nu depinde de natura substantei de lucru.

Teorema 2

Randamentul unei masini termice care functioneaza ireversibil este mai mic decat al unei masini ce functioneaza dupa un ciclu Carnot reversibil intre aceleasi limite de temperatura.

Enuntul lui Clausius

Caldura nu trece in mod spontan de la un corp mai rece la unul mai cald.

Pentru a justifica aceasta afirmatie pornind de la enuntul de baza, se considera un sistem izolat S_t format din doua subsisteme S_c si S_r avand temperaturile T_r<T_c si care pot schimba energie numai prin caldura. Pentru un proces termodinamic elementar bilantul energetic si entropic conduce la:

deoarece W=0.

Cum ireversibilitatea este datorata contactului intre subsisteme:

Cantitatie de caldura primite de cele doua subsiteme fiind de semne opuse:

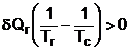
Cum T_c>T_r,

deci corpul mai cald cedeaza caldura corpului mai rece.

Enuntul lui Thomson

In cursul unui proces ciclic, un sistem in contact cu o singura sursa, nu poate decat sa primeasca lucru mecanic si sa cedeze caldura. Altfel spus, o masina monoterma este irealizabila.

Pentru a stabili valabilitatea enuntului vom aplica bilantul energetic si entropic sistemului dupa un ciclu. Daca W si Q sunt repectiv lucrul mecanic primit (algebric) si caldura iar T este temperatura sursei, se obtine:

Cum T>0, rezulta Q<0 si W>0, ceea ce confirma enuntul.

3.                  Stare stationara si stare de echilibru

Starea termodinamica a unui sistem este stationara daca parametrii macroscopici ce o definesc nu evolueaza in timp cu toate ca exista o productie de entropie in sistem S_prod>0.

Productia de entropie din sistem se traduce prin existenta unui gradient nenul al unor variabile intensive, si este compensata prin schimb deoarece S=const.

Un sistem este in echilibru termodinamic daca este stationar si productia sa de entropie este nula. Bineinteles productia de entropie nula traduce uniformitatea tuturor marimilor intensive.

Evolutia unui sistem este reversibila daca productia de entropie este nula, ceea ce permite sa consideram aceasta evolutie ca o succesiune de stari de echilibru termodinamic.

Pentru o evolutie reversibila, intre doua stari de echilibru, bilantul entropic si energetic se scriu:

si considerand constanta energia cinetica si energia primita din exterior

deducem deci ca in sisteme inchise entropia este o functie de U si V si ca:

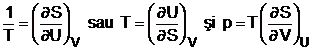
Pentru a ilustra relatiile de mai sus vom calcula variatia de entropie pentru un gaz perfect ce evolueaza reversibil intre doua stari de echilibru. Intre doua stari infinit apropiate putem scrie:

unde C_V este caldura molara la volum constant. Integrand intre starile de echilibru initiala si finala, obtinem:

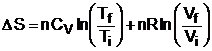
4.                  Bilant entropic local

Consideram un sistem termodinamic de volum V, delimitat de suprafata de separatie S. Bilantul entropic al sistemului este:

sau

unde  este densitatea, s entropia masica, vectorul curent volumic de entropie si productia volumica de entropie pe unitatea de timp.

Aplicant teorema Ostrogradski obtinem:

si cum volumul este oarecare, se deduce ecuatia locala:

(1.21)

In cazul particular al unei evolutii reversibile, si ecuatia locala a bilantului entropic devine:

(1.22)