Legea inductiei electromagnetice

Experienta arata ca variatia in timp a unui camp magnetic are ca efect aparitia unui camp electric si invers, variatia in timp a unui camp electric duce la aparitia unui camp magnetic.

Legea inductiei electromagnetice, stabilita experimental, determina cantitativ efectul electric al campului magnetic si conditiile in care un camp magnetic produce camp electric. Legea inductiei electromagnetice este o lege general valabila, fara restrictii. Ea se poate exprima prin doua modele identice ca rezultat, dar formal diferite: un model integral (global, relativ la orice contur inchis Γ dintr-un camp Ω) si altul local (relativ la orice punct P din campul Ω).

Modelul global al legii inductiei electromagnetice

Fie Γ un contur inchis, oricare, din domeniul Ω de existenta a unui camp electromagnetic. Se numeste inductie electromagnetica fenomenul producerii unei tensiuni electromotoare e_Γ intr-un circuit (conductor) in care a fost ales conturul Γ, sau a unei tensiuni electrice u_Γ in cazul general al unui contur inchis Γ aflat indiferent in ce mediu (conductor, izolant sau/si vid), datorita variatiei in timp a fluxului magnetic prin orice suprafata Σ_Γ ce se 'sprijina' pe conturul Γ (adica cu FrΣ_Γ = Γ). Sensul t.e.m. e_Γ , sau a tensiunii electrice in lungul curbei u_Γ , este astfel incat efectele lor sa se opuna cauzei care le-a produs, aceasta in virtutea unui principiu universal al echilibrului natural (care nu admite cresteri paroxistice), cunoscut si sub forma unitatii dialectice dintre contrarii (enuntata de Hegel), adica dintre actiune si reactiune sau dintre cauza si efect. Acesta este aspectul calitativ al fenomenului inductiei electromagnetice.

Legea inductiei electromagnetice exprima cantitativ acest fenomen determinand ca: tensiunea electromotoare e_Γ produsa prin inductie electromagnetica in lungul unui contur inchis Γ este egala cu viteza de scadere a fluxului magnetic prin orice suprafata S_G marginita de conturul G, ceea ce se exprima prin modelul:

(1.81)                        G W cu G = FrS_G ,

care reprezinta forma globala a legii inductiei electromagnetice si in care d/dt reprezinta derivata substantiala in raport cu timpul (v. § 9.1.2) a fluxului magnetic, semnul minus al acestei derivate modeland principiul actiunii si reactiunii. (Se mai poate da si urmatoarea explicatie: daca G este un contur inchis intr-un corp conductor de pilda, o spira conductoare inchisa, adica o bucla de curent atunci in spira/bucla, t.e.m e_G determina o stare electrocinetica, descrisa de un curent electric i_G , care prin efectul ei magnetic conform legii circuitului magnetic /v. § 1.3.8 va crea un camp magnetic al carui flux magnetic va actiona ca element de reactie fata de fluxul primar prin a carui variatie, ca element de actiune, s-a indus t.e.m e_G care a produs starea electrocinetica ce a dus la fluxul magnetic de reactie etc.). Se pot da si alte justificari asa cum este cea energetica prezentata in cartea Timotin, A.,Hartopan, V.(l964).

Legea (1.81) se scrie, mai simplu, si in forma:

e = dj/dt , (1.81')

o astfel de tensiune electromotoare numindu-se tensiune electromotoare de inductie.

Tinandu-se seama de definitia t.e.m. (1.45), reiese ca e_G este rezultatul circulatiei intensitatii unui camp electric, produs de variatia in timp a fluxului magnetic, care se noteaza cu Ē_s si se numeste camp electric de inductie sau camp solenoidal (de unde si indicele s). Atunci, conform relatiei (1.49) si in lipsa unui camp electric imprimat , t.e.m. de inductie electromagnetica e_Γ se poate exprima prin circulatia lui de-a lungul conturului inchis Γ:

(e)

Pe de alta parte, avandu-se in vedere definitia (l .36) a fluxului magnetic, rezulta ca membrul din dreapta al legii (1.81) se poate scrie sub forma:

. (φ)

Atunci, inlocuindu-se in modelul (1.81) membrul din stanga cu expresia (e) si cel din dreapta cu expresia (φ), rezulta o noua formula globala (integrala) a legii inductiei electromagnetice si anume:

. (1.81')

In legatura cu aceste doua modele, formal diferite (1.81) si (1.81'), ale legii inductiei electromagnetice sunt necesare cateva precizari:

- conturul inchis Γ poate fi unul oarecare din domeniul Ω de existenta al campului electromagnetic, insa in aplicatiile practice ale electrocineticii Γ se alege in lungul unui conductor electric filiform (de exemplu in lungul spirelor unei bobine electrice, care in engleza numindu-se solenoid / cuvant de provenienta latina / a facut sa se dea lui denumirea de camp solenoidal, avand in vedere ca primul fizician care a studiat fenomenul inductiei electromagnetice a fost englezul Faraday, in anul 1831, experimentele facandu-se in special pe bobine / solenoizi). in principiu, conturul inchis Γ poate fi ales -ca un caz general- in orice fel de mediu (conductor, izolant sau/si vid) si poate avea orice forma;

- daca mediul considerat este in miscare, conturul Γ este atasat corpurilor in miscarea lor;

- sensul de integrare pe conturul Γ din relatia (1.81'), adica sensul elementului de curba orientat , si sensul elementului de arie orientat din expresia fluxului al relatiei (1.81'), mai precis sensul versorului normalei localei la suprafata Σ_Γ prin care se determina fluxul magnetic, sunt asociate dupa regula sistemului drept (asa-zisa 'regula a burghiului drept'). Semnul "minus" din modelul (1 .81') reflecta faptul ca derivata lui si e_Γ au sensurile asociate invers regulii sistemului drept, datorita necesitatii de modelare a principiului actiunii si reactiunii ce intervine in acest fenomen.

Daca, in continuare se efectueaza derivata din membrul drept al formei (1.81') a legii inductiei electromagnetice, care reprezinta in fapt derivata substantiala (materiala) a fluxului magnetic in raport cu timpul (v.§ 9. l .2), deoarece vectorul inductiei magnetice este o functie de timp si de punct P (cu coordonatele x, y, z intr-un sistem de referinta cartezian), adica atunci derivata din membrul drept al legii (1.81') este data de relatia (9.44) fiind:

,

indicele f atasat operatorului de derivare indicand faptul ca se refera la flux, astfel ca forma integrala (1.81') a legii inductiei electromagnetice ia forma, stiind ca in conformitate cu legea fluxului magnetic ( l .69' ) div:

()                  

Modelul local al legii inductiei electromagnetice

Daca proprietatile fizice locale indeplinesc conditiile de continuitate, atunci aplicandu-se formula lui Stokes (9.28), potrivit careia circulatia unui vector este egala cu fluxul rotorului acelui vector printr-o suprafata delimitata de conturul circulatiei (v. § 9.1.2) membrul stang al legii (1.81'') devine:

astfel ca legea poate fi rescrisa sub forma urmatorul model:

(1.81^IV)                

Deoarece suprafata se alege arbitrar, putand fi oricare suprafata ce indeplineste conditia rezulta ca modelul ^IV) poate fi scris si sub forma:

(1.82)                               ,

unde este viteza de deplasare a conturului inchis in domeniul al campului electromagmetic, asociata unor corpuri.

Modelul (1.82) reprezinta, forma locala generala a legii inductiei electromagnetice. Pentru corpurile imobile, deci in punctele in care , legea (1.82) are forma:

Legea inductiei electromagnetice sub forma locala (1.82) arata ca in cazul campului electromagnetic variabil in timp poate apare, la orice variatie a campului magnetic, un camp electric a carei intensitate (ce a fost notata cu) are rotorul diferit de zero, adica se produce un camp electric rotational . Deci campul electric indus (campul solenoidal), conditionat de variatia in timp a campului magnetic, are liniile de camp inchise sau aproape inchise (adica inchise la infinit) si atunci adica integrala curbilinie a intensitatii campului electric solenoidal intre doua puncte din campul, A si B, depinde de drum, deci de curba dintre A si B, ceea ce inseamna ca in campul solenoidal nu se poate definii un potential electric in sensul aratat in paragraful 1.2.2.

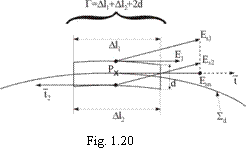
Campul solenoidal pe suprafetele de discontinuitate

In cazul suprafetei de discontinuitate , legea inductiei electromagnetice -sub forma - se aplica unui contur inchis foarte mic, in forma de dreptunghi (fig.1.20) cu cu laturile si paralele cu situate de o parte si de alta lui , si avand cu d .

Daca d 0, atunci si orice suprafata marginita de , , va tinde catre zero si -in aceste conditii- fluxul magnetic prin si deci si derivatele lui vor tinde catre zero. In aceasta situatie idealizata de trecere la zero, conturul dreptunghiular devine strans alipit de suprafata de discontinuitate S_d in jurul unui punct (v.fig.1.20), ceea ce permite ca legea (1.81^") sa se scrie sub forma:

adica:

sau, deoarece la limita:

si

iar

,

unde versorii tangentelor la pe si sunt , astfel ca:

de unde rezulta:

sau

Insa si care sunt componentele tangentiale la suprafata ale intensitati campului electric solenoidal in , rezultand in final:

ceea ce arata ca, la trecerea printr-o suprafata de discontinuitate, componenta tangentiala a campului electric solenoidal se conserva. In consecinta liniile de camp electric solenoidal (si in general liniile de camp electric - v. cap.2) se refracta la trecerea printr-o suprafata de discontinuitate.