Modele si analiza temporale

Aceasta prima parte este consacrata sistemelor lineare continue monovariabile, adica sistemelor care prezinta o singura intrare u(t) si o singura iesire y(t). Se va utiliza o abordare intrare-iesire care nu tine seama de variabilele de stare ale modelului sistemului. Dinamica sistemului este descrisa in mod unic de o dependenta a marimii de iesire fata de marimea de intrare.

y(t)=f[t, u(t)]

1 Caracterizarea dinamicii unui sistem

Un sistem este cu raspuns instantaneu sau static sau cu transfer direct intrare-iesire daca, la un moment t oarecare, iesirea poate fi determinata intr-o maniera unica de valoarea intrarii in acelasi moment; putem scrie:

(1)

Reprezentarea grafica a acestei relatii s numeste caracteristica statica a sistemului.

Un exemplu elementar corespunde cazului unei rezistente electrice: marimea de intrare este tensiunea u(t) aplicata la bornele sale, in timp ce curentul i(t) prin rezistenta constituie marimea de iesire.

S-a obtinut un sistem static linear cu caracteristica rectilinie.

Daca marimea de iesire este puterea P(t) disipata prin rezistenta, sistemul static cu intrarea u(t) si iesirea P(t) este deci nelinear.

(caracteristica parabolica)

Cum am vazut deja in capitolul 1, caracterul dinamic al sistemelor este descris printr-un ansamblu de variabile interne reunite in vectorul de stare.

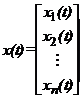(2)

O reprezentare intrare-iesire apare oarecum ca rezultatul compunerii functiei de tranzitie stare-iesire, , cu functia de tranzitie a starilor, , permitand eliminarea vectorului de stare:

(3)

De fapt, acest demers este realizat implicit, deoarece functia f este determinata direct plecand de la legile care modeleaza comportamentul sistemului.

Atunci cand timpul intervine explicit (si nu prin intermediul variabilelor u(t)si x(t), se spune ca sistemul este variant (sau evolutiv) ). Daca t nu intervine explicit, cazul cel mai frecvent intalnit in aplicatii, se spune ca sistemul este invariant (sau stationar)

Exemplul 1. sistem dinamic invariant

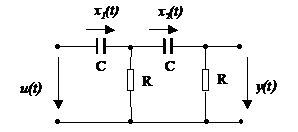
Pentru a exprima y(t), trebuie sa consideram tensiunile x₁(t) si x₂(t) de la bornele condensatoarelor, suficiente pentru a defini starea interna a retelei la un moment dat:

y(t) = u(t) - x₁(t) - x₂(t)

Aceste variabile de stare sunt definite prin intermediul a doua ecuatii diferentiale de ordinul unu:

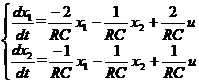(4)

Utilizand ecuatiile (4), structura acestui sistem poate fi reprezentat prin urmatoarea schema generala:

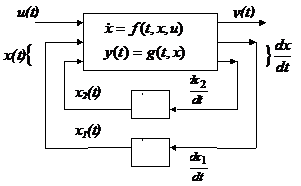
Aceasta structura se potriveste perfect cu descrierea sistemelor care sunt guvernate de ecuatii diferentiale ordinare.

Derivand de doua ori expresia algebrica

(5)

si utilizand de fiecare data ecuatiile (4) si (5) pentru a elimina variabilele , aceasta devine:

(6)

Obtinem astfel un model intrare-iesire al sistemului considerat. Iesirea y(t) este definita rezolvand ecuatia (6) pentru conditiile t_o, x₁(t_o) si x₂(t_o) bine precizate.

2 Reprezentarea unui sistem dinamic

Intr-un demers de modelare temporala, un sistem dinamic monovariabil poate fi descris in doua moduri clasice:

1. Reprezentarea de stare

In continuare se va utiliza o notatie matriciala care face legatura intre vectorul de stare x(t), variabilele de intrare u(t) (vectorul de intrare) si variabilele de iesire y(t) (vectorul de iesire).

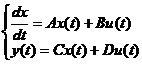
Este vorba de o ecuatie diferentiala vectoriala de ordinul unu. Pentru exemplul anterior, avem:

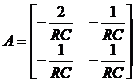matrice patrata (2×2)

matrice coloana (2×1)

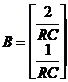matrice linie (1×2).

Acest punct de vedere este si mai interesant in cazul intrarilor si iesirilor multiple

Reprezentarea sub forma ecuatiei diferentiale de transfer

Se inlocuiesc cel n ecuatii diferentiale de ordinul intai cuplate, printr-o ecuatie diferentiala unica de ordinul n, care leaga iesirea y(t) si cele n derivate ale ei in raport cu timpul.

.

Se obtine astfel ecuatia diferentiala de transfer (sau EDT) sub urmatoarea forma:

, (sistem variant) (7)

sau

, (sistem invariant) (8)

De exemplu, ecuatia (6) este o EDT care caracterizeaza un sistem invariant, deoarece coeficientii ecuatiei diferentiale nu depind de t.

Ecuatiile (7) sau (8) nu determina intr-un mod univoc iesirea y(t) a sistemului considerat. Acestea trebuie sa fie insotite de conditiile initiale care caracterizeaza starea initiala a sistemului.

O EDT impreuna cu conditiile initiale constituie un model temporal al sistemului dinamic, a carui solutie este unica.

3. Ordinul si clasa unui sistem dinamic

Prin definitie, ordinul unui sistem este egal cu numarul minim n al variabilelor sale de stare. De asemenea, reprezinta cel mai mare grad al derivatelor iesirii y(t), in raport cu timpul, in ecuatia diferentiala d transfer.

Pentru a defini clasa unui sistem invariant, se va considera cazul in care intrarea u(t) a sistemului este constanta, adica:

.

Daca sistemul este asimptotic stabil, vom obtine la finalul unui timp "indeajuns de lung" o iesire permanent constanta. . In acest caz avem de-a face cu un regim permanent constant.

O stare de echilibru E(,), pentru un sistem invariant, corespunde unui cuplu de valori si , astfel incat ecuatia (8) devine:

Aceasta lege care face legatura intre intrare si iesirea in regim stationar defineste caracteristica statica a sistemului.

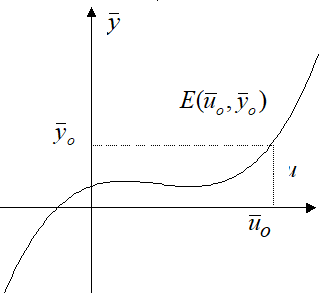
Sistem de clasa zero:

Spunem ca sistemul (8) este de clasa zero daca iesirea y(t) si intrarea u(t) figureaza explicit in ecuatia diferentiala de transfer. In acest caz, se poate defini caracteristica sa statica.

Sistem de clasa k:

Spunem ca sistemul (8) este de clasa k, daca intrarea u(t) figureaza explicit in ecuatia diferentiala de transfer, dar nu figureaza.

In acest caz, nu se poate defini caracteristica sa statica.

Utilizand notatia

ecuatia diferentiala de transfer se scrie:

S-a obtinut un nou sistem cu iesirea v(t), de ordin (n-k) si clasa 0.

Sistemul initial este obtinut prin dispunerea a k integratoare pe iesirea sistemului de clasa 0.

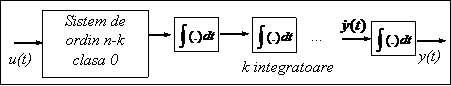
Sistem de clasa - k

Spunem ca sistemul (8) este de clasa - k daca iesirea y(t) figureaza explicit in ecuatia diferentiala de transfer, dar nu figureaza.

Utilizand notatia

ecuatia diferentiala de transfer se scrie:

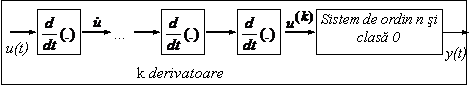
S-a obtinut un nou sistem cu intrarea w(t), de ordin egal cu n si de clasa 0.

Astfel, toate sistemele dinamice pot fi descompuse intr-un subsistem de clasa 0 precedat de k₁ derivatoare si urmat de k₂ integratoare. De aceea, in cele ce urmeaza, ne vom ocupa in principal de analiza sistemelor de clasa zero.

3. Sisteme dinamice lineare continue

Vom desemna prin sistem linear continuu (SLC) toate sistemele dinamice ale caror ecuatie diferentiala de transfer, in forma implicita

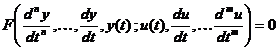
este o ecuatie diferentiala lineara:

cu

Pe de alta parte, daca coeficientii a_k sunt constanti, se obtine un SLC invariant (SLCI)

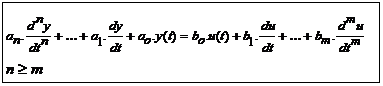
(9)

Putem determina la momentul t raspunsul y(t) al sistemului la o excitatie cunoscuta u(t), daca cunoastem starea initiala x(t₀) a sistemului la un moment de timp anterior oarecare t₀. Aceasta stare poate fi caracterizata prin valorile initiale date (in numar de n pentru un sistem de ordin n)

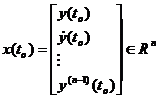
De exemplu, cunoscand intrarea u(t), sistemul descris prin EDT:

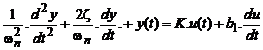
poseda o solutie unica daca cunoastem si

De acum inainte ne vor interesa mai ales sistemele dinamice lineare continue invariante (SLCI).

4. Linearizarea locala a unui sistem dinamic nelinear

Pentru SLCI exista instrumente de analiza si de sinteza mult mai dezvoltate decat pentru sistemele nelineare. Atunci cand un sistem nelinear nu prezinta nelinearitati esentiale, putem practic sa linearizam local in jurul unui punct de echilibru. Sa consideram un sistem dinamic continuu, a carui ecuatie diferentiala de transfer nu este lineara:

Se presupune ca comportamentul sau este descris de ecuatia diferentiala de transfer implicita:

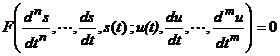(10)

Prezentam in continuare un exemplu de astfel de ecuatie:

Fie E( ) o stare de echilibru a sistemului considerat. Avem:

Presupunem ca F este o functie continua si derivabila, in raport cu toate argumentele sale, in vecinatatea acestei stari de echilibru.

Intotdeauna putem sa consideram functiile si astfel incat:

Ecuatia (10) poate fi rescrisa sub urmatoarea forma:

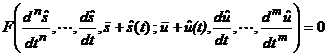
Notam:

si

In punctul de echilibru avem:

(11)

In vecinatatea acestei stari de echilibru obtinem:

Efectuam o dezvoltare in serie Taylor in vecinatatea starii de echilibru E(

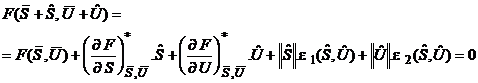
Tinand cont de ecuatia (11), obtinem:

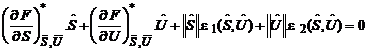
Neglijand termenii de ordinul doi, ajungem la:

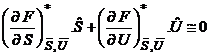
Fie in forma explicitata:

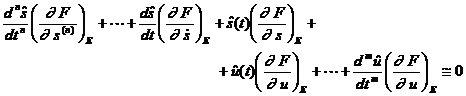
Suntem in prezenta unei ecuatii diferentiale de transfer, lineara cu coeficienti constanti, descriind 'asimptotic' comportamentul dinamic al sistemului nelinear in vecinatatea punctului de echilibru E( ). Acest nou model, corespunzator unui SLCI, este valabil numai local pentru semnale de mica amplitudine.

Exemplul 2: Se considera un model simplificat care descrie comportamentul unui motor electric de curent continuu, comandat prin curentul inductorului notat x(t), tensiunea indusului u₀ fiind mentinuta constanta.

Notam cu w(t) viteza de rotatie a arborelui motorului,

J : inertia rotorului,

f : coeficientul de frecare vascoasa asupra sarcinii,

k : coeficientul de cuplu si de forta contra-electromotoare,

A : coeficientul de proportionalitate intre fluxul F si curentul inductorului,

R : rezistenta electrica a indusului.

In acest context, EDT-ul care leaga marimea de iesire w(t) de intrarea de comanda x(t) poate fi scrisa sub urmatoarea forma:

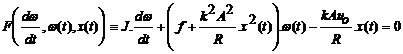(12)

Din cauza termenului sistemul dinamic este nelinear. Caracteristica statica a acestui sistem, de clasa 0, este furnizata de urmatoarea ecuatie algebrica:

care permite exprimarea valorii constante a iesirii in functie de valoarea constanta a intrarii:

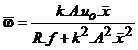
In cazul in care u_o > 0, obtinem caracteristica statica urmatoare:

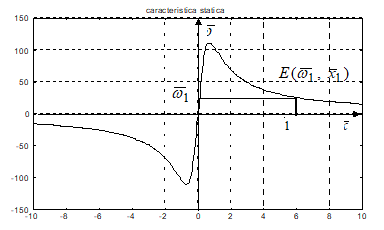
Pentru variatii mici ale marimii de intrare , in vecinatatea punctului de echilibru , variatiile marimii de iesire vor fi definite intr-o maniera aproximativa de solutia EDT (12):

linearizarea in vecinatatea punctului de echilibru E₁.

Ecuatia linearizata se poate scrie:

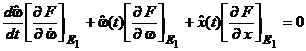
unde

.

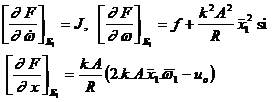Am obtinut o ecuatie diferentiala lineara, cu coeficienti constanti, de ordinul intai, caracterizata de o constanta de timp t₁ si o amplificare de regim stationar K₁ dependenta de punctul de echilibru E₁:

,

cu

si

.
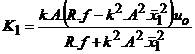