|
|
|
Ecuatia lui Schrodinger
Admitand
existenta unui fenomen ondulatoriu asociat particulei in miscare,
Schrodinger a trecut la o descriere cantitativa a acestuia, asociindu-i o
functie de coordonate si timp 
ca oricarui
fenomen ondulatoriu cunoscut pana atunci. Functia nou introdusa
se numeste functie de unda.
Tinand seama ca optica geometrica este un caz limita al opticii ondulatorii, Schrodinger a cautat sa extinda analogia lui Hamilton intre mecanica clasica si optica fasciculelor, cautand analogul opticii ondulatorii pentru miscarea particulelor, adica mecanica ondulatorie, in concordanta cu teoria lui de Broglie. Pentru ecuatiile diferentiale ale opticii ondulatorii trebuie sa existe ecuatii analoage care sa descrie miscarea particulelor in cadrul mecanicii ondulatorii. Analizand ecuatia fundamentala de propagare a undelor:
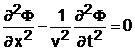(4.13)
unde v viteza de faza a acesteia, Schrodinger a aratat necesitatea introducerii functiei de unda care sa verifice o ecuatie asemanatoare ecuatiei (4.13), in care viteza de faza sa fie:
(4.14)
in care E este energia totala, iar U energia potentiala a particulei. Relatia (4.14) a fost obtinuta de Schrodinger pe baza analogiilor dintre principiile lui Fermat si Hamilton si utilizand teoria de Broglie. O prima forma a ecuatiei cautate este:
Ecuatia nu este complet satisfacatoare, datorita faptului ca in scrierea coeficientilor intervin parametri ca impulsul sau energia si astfel nu poate fi obtinuta o solutie generala. Prin urmare, ecuatia cautata ar trebui sa fie liniara, pentru ca solutiile sa poata fi suprapuse in scopul explicarii unor fenomene ca interferenta si difractia. De asemenea, ar trebui ca in coeficientii ecuatiei sa nu intervina decat constante, care sa permita constructia unei solutii generale. Cum ecuatia diferentiala ar trebui sa admita solutii de tipul:
onsecinte.
