|
|
|
Deseori, pentru analiza unui sistem, consideram ca semnale de intrare semnale canonice, cum ar fi treapta unitara sau semnalul sinusoidal. Daca sistemul considerat este asimptotic stabil in anumite conditii date, constatam ca raspunsul corespunde, dupa un interval de timp indelungat, unui semnal canonic, uneori de acelasi tip ca a celui de intrare. In acest caz, consideram ca sistemul se afla in regim permanent, caruia ii corespunde raspunsul permanent ypm(t).
Astfel, solutia y(t) mai poate fi descompusa intr-o alta forma:
,
ytr(t) fiind raspunsul tranzitoriu al sistemului care are urmatoarea proprietate:
.
Subintelegem existenta, in evolutia sistemului, a unui regim tranzitoriu de durata 'finita', care, o data terminat, lasa loc regimului permanent. In practica, consideram ca regimul tranzitoriu se termina dupa un timp 'suficient' de lung pentru a putea fi neglijat.
Daca reluam sistemul considerat in exemplul 2.3 cu aceeasi stare initiala, si cu raspunsul la treapta unitara:
,
vom constata ca
Putem deci considera urmatoarea descompunere a raspunsului sistemului:
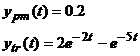
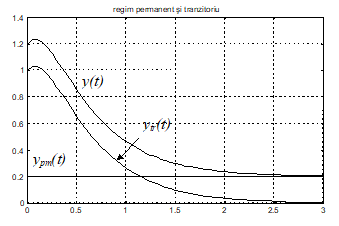
Desi exista o anume dificultate matematica in definirea regimurilor tranzitoriu si permanent, cele doua concepte sunt foarte importante in automatica.
In capitolul 7, consacrat sintezei sistemelor, se va vedea ca anumiti indici de performanta sunt definiti in raport cu aceste regimuri.
Daca
sistemul este asimptotic stabil, atunci exista un regim permanent constant
caracterizat prin punctul de echilibru E(
,
), pentru care ecuatia diferentiala (2.9) se reduce la o simpla relatie de
proportionalitate intre 
si :
unde coeficientul K definit prin:
poarta numele de amplificare in regim stationar a sistemului.
