Ecuatiile de echivalenta

Se considera eforturile interioare : N, T_y, T_z, M_t, M_iy, M_iz ca rezultante datorata tensiunilor.

Se va scrie echivalenta intre eforturi si tensiunile ce actioneaza pe sectiunea transversala. σ_xxdA, dT_y = τ_xydA, dT_z = τ_xzdA

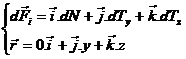
S-a luat elementul de arie  dA = dy.dz, in centrul lui se afla punctul

Q (0;y;z), iar GQ = r ( vectorul de pozitie al punctului Q ), pentru toata sectiunea transversala se obtin rezultatele prin integrare, din figura 19.

tinand cont de sensurile axelor GX;GY;GZ  va rezulta:

dM_tx= (yτ_xz-zτ_xy)dA, dM_iy=zσ_xxdA, dM_iz= yσ_xxdA

, ,

, de unde au rezultat urmatoarele ecuatii de echivalenta:

, ,

, ,