ARDEREA COMBUSTIBILILOR GAZOSI

1 Introducere

Arderea eficienta a combustibililor gazosi reprezinta o problema de mare importanta, avand in vedere ponderea mare a gazelor naturale in structura generala a consumului de combustibil [9, 30, 33, 35, 40, 63, 91, 115].

In functie de marimea componentilor timpului de ardere, arderea se considera cinetica, difuziva sau intermediara.

In general, timpul total de ardere se compune din doua parti: timpul necesar realizarii contactului fizic intre combustibil si aerul necesar arderii si timpul necesar desfasurarii reactiei chimice .

Cand componentele care reactioneaza sunt in stare gazoasa, este timpul de amestecare.

Cand timpul de amestecare , este cu mult mai mic decat timpul , procesul de ardere este determinat de viteza de reactie chimica, arderea in acest caz este denumita ardere cinetica.

Conform terminologiei utilizate in literatura de specialitate, in cazul in care timpul este cu mult mai mare decat cel de reactie chimica , arderea este considerata difuziva; iar in cazul in care cei doi timpi sunt comparabili, arderea este denumita intermediara.

2 Bazele teoretice ale arderii combustibililor gazosi

In general procesul de ardere este dat de reactia chimica a doua elemente, combustibilul si oxigenul [9, 30, 33, 35, 63, 115].

Reactia chimica intre substantele A si B, care decurge cu formarea produselor M si N, poate fi descrisa de ecuatia stoichiometrica, care se prezinta sub forma:

, (1)

in care:

A; B; M; N reprezinta formulele chimice ale substantelor respective;

a, b, m, n sunt coeficientii stoichiometrici;

Q - efectul termic al reactiei.

Pentru cele mai raspandite gaze combustibile utilizate in tehnica arderii, rezulta urmatoarele ecuatii stoichiometrice:

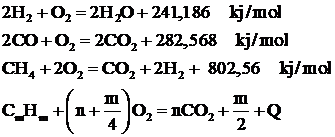
Conform legii actiunii maselor, viteza reactiilor chimice depinde de concentratia substantelor care reactioneaza si de temperatura.

Intr-o forma generala aceasta viteza poate fi scrisa sub forma:

, (2)

in care: w este viteza reactiei chimice, care se considera ca este egala cu viteza de scadere a concentratiilor substantelor respective; C - concentratia substantelor care reactioneaza; T - temperatura initiala.

Dependenta constantei reactiei chimice de temperatura, este data de legea lui Arhenius, care are forma:

, (4)

in care:

k₀ - constanta;

E - energia de activare, kj/mol;

R - constanta universala a gazelor, ;

T - temperatura absoluta, ⁰K.

Constanta k₀, se poate lua proportionala cu , desi unii cercetatori considera ca este independenta de temperatura.

1.2 Mecanismul de reactie in lant in procesele de ardere

Legile de desfasurare a reactiilor chimice in procesele de ardere difera mult de legile clasice ale cineticii chimice. Cauzele acestei abateri se datoreaza faptului ca reactiile chimice in procesele de ardere, nu au loc conform ecuatiilor stoichiometrice de oxidare . Mecanismul de reactie in procesul de ardere, conduce la aparitia in flacara a radicalilor, atomilor sau moleculelor cvasistabile cu energie mica de activare [9, 33, 35, 40, 63, 115].

Este de remarcat ca in afara produsului final de reactie, ramane in amestec si o cantitate de produse intermediare active, care continua lantul de transformari.

Cea mai studiata reactie in lant este cea dintre hidrogen si oxigen.

Conform ecuatiei stoichiometrice rezulta:

ceea ce arata ca reactia este de gradul trei.

Conform literaturii de specialitate, un atom de hidrogen format in amestec poate reactiona cu o molecula stabila de oxigen, conform schemei:

H H

O+H₂ OH+H₂ H₂O

H+O₂ H₂O (9)

OH+H₂

sau:                                                      H

Astfel rezulta ca, la fiecare atom de hidrogen se formeaza, intr-un ciclu doua molecule de apa si trei noi atomi de hidrogen, care la randul lor, pot dezvolta trei cicluri asemanatoare, daca nu are loc reactia de anihilare a centrilor activi, conform relatiei:

. (10)

Reactia in lant poate fi de tip ramificat, cand intr-un ciclu se formeaza mai multi centri activi sau de tip neramificat, cand numarul de centri activi formati pe ciclu este egal cu cel initial in ciclu.

Viteza de formare a centrilor activi in reactia in lant este data de relatia:

, (11)

in care:

w_a este viteza de formare a centrilor activi intr-un ciclu;

c_a - concentratia centrilor activi;

f - constanta de ramificare a lantului;

g - constanta de rupere a lantului;

- viteza de ramificare a ciclurilor;

- viteza de rupere a lantului.

Legea de variatie in timp a concentratiei centrilor activi, care are forma:

. (12)

3.1 Schimbul de masa si de caldura in flacarile difuzive laminare

3.1.1 Ecuatiile proceselor de schimb de masa si de caldura

In prezent datorita lucrarilor fizicienilor S.R. de Groot, J. Prigogine, L. Onsager, A.H. Lakov s-a creat posibilitatea de aplicare a teoriei fenomenologice in studiul proceselor de schimb de masa si caldura in domeniul curgerii laminare, teorie care se bazeaza pe rezultatele obtinute de cercetarile efectuate in domeniul termodinamicii proceselor ireversibile [9, 30, 33, 35, 40, 63, 91, 115].

Conform termodinamicii proceselor ireversibile fluxul specific de masa este dat de relatia:

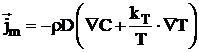, (16)

in care:

D este coeficientul de difuzie moleculara;

r - densitatea sistemului;

C - concentratia;

k_T - constanta de termodifuzie;

T - temperatura

Fluxul specific de caldura conform 7,8 , este dat de relatia:

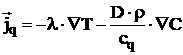, (17)

in care:

este coeficientul de conductibilitate termica.

Conform teoriei cinetico-moleculare a gazelor ideale coeficientul de difuzie moleculara este dat de relatia:

, (19)

- conductivitatea termica

Daca se utilizeaza coeficientul de difuzivitate a temperaturii fluidului a:

, (20)

- coeficientul de vascozitate dinamica,

,

din care rezulta vascozitatea cinematica ,

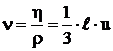, , (21)

In concluzie, pentru gazele ideale, invariantii Prandtl, , Schmidt, si Lewis, , sunt egali cu unitatea, in timp ce pentru gazele reale difera de unitate. Este de remarcat ca, acesti invarianti au un rol deosebit in procesele de transfer de masa si de caldura.

In cazul proceselor de ardere laminara, ecuatia de transport de masa are forma:

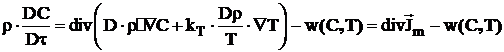(22)

in care termenul w(C,T) reprezinta viteza de reactie chimica care depinde atat de temperatura cat si de concentratii, iar este derivata substantiala a concentratiei.

Ecuatia transferului de caldura in cazul arderii difuziv laminare, conform 30 , in care se vor neglija termenii disipativi si se va considera sistemul izolat adiabatic, se poate scrie sub forma:

, (24)

Se mai adauga ecuatia continuitatii, care are expresia:

,            (25)

si ecuatia Navier-Stokes, in care se neglijeaza termenii disipativi si care conform 30 are forma:

, (26)

3.1.2 Schimbul de masa si caldura in flacarile difuziv turbulente ale gazelor combustibile

Schimbul de masa si de caldura in jeturile turbulente este intensificat puternic, fata de curgerea laminara deoarece in afara schimbului molecular, apare si un schimb de turbioane, care trec dintr-un strat in altul [9, 33, 35, 63, 91, 115].

Conform teoriei lui Prandtl, valoarea medie patratica a pulsatiei vitezei 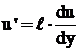, rezulta conform relatiei (29), ca

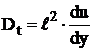. (30)

Avand in vedere ca, scara turbulentei dupa teoria lui Taylor, este , rezulta dupa teoria acestuia ca:

. (31)

Astfel, prin analogie, se poate vorbi de coeficient turbulent de conductie si de vascozitate cinematica turbulenta n_t

3.1.3 Schimbul de masa si caldura intre jeturile de gaze

combustibile si aer

Este de mentionat faptul ca, procesul de amestecare dintre jetul de combustibil si aerul necesar arderii are o influenta majora asupra caracteristicilor flacarii (lungime, stabilitate si radiatie) [9, 30, 35, 40, 63, 115].

Un jet este caracterizat de trei zone, care se pot distinge, conform figurii 2:

Fig. 2 Zonele jetului turbulent liber cu viteza ambianta nula

Cele trei zone ale jetului sunt:

- zona initiala, , in care se stabileste un nucleu potential, in care se conserva toate marimile initiale ale jetului;

- zona de tranzitie , in care are loc o redistribuire ale marimilor initiale in sectiunile transversale:

- zona de baza in care distributia vitezelor, concentratiilor si temperaturilor in sectiunile transversale ale jetului sunt de tipul functiilor Gauss.

In ceea ce priveste zona de tranzitie, aceasta este foarte mica, fapt pentru care in unele cercetari este neglijata.

Functiile de distributie in sectiunile transversale din zona de baza a jeturilor turbulente axial simetrice libere sunt conform literaturii de specialitate:

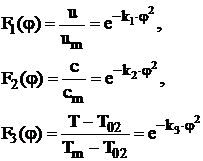(33)

unde:

u - este viteza intr-un punct oarecare dintr-o sectiune oarecare din zona de baza a jetului:

v_m - viteza pe axa jetului, in aceeasi sectiune;

c - concentratia in punctul de coordonate (x,y) al unei sectiuni transversale din zona de baza a jetului;

c_m - concentratia pe axa jetului, in aceeasi sectiune;

- temperatura pe granita jetului;

T_m - temperatura pe axa jetului;

T - temperatura dintr-un punct oarecare din aceeasi sectiune a jetului;

- ordinata adimensionala;

a - coeficientul de structura a jetului, coeficient ce depinde de unghiul de evazare a jetului a

. (34)

4.1 Viteza de propagare a frontului de flacara a combustibililor gazosi in cazul curgerii laminare

Aceasta viteza este cunoscuta in literatura de specialitate sub numele de viteza normala de propagare a frontului de flacara sau viteza normala de ardere .

Pe baza teoriei termice, Kolmogorov, Petrovski si Piscunov arata ca viteza normala de ardere a flacarilor de gaze combustibile se poate determina cu relatia:

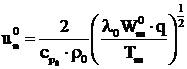,                            (48)

Pentru determinarea valorii maxime a vitezei normale de ardere a unui amestec de mai multe gaze combustibile cu aerul de ardere, se poate utiliza relatia:

, (49)

In practica, viteza normala de propagare a frontului de flacara se determina cu arzatorul Bunsen, folosind flacara laminara, la care frontul de flacara este dat de aria laterala a conului de flacara, conform figurii alaturate:

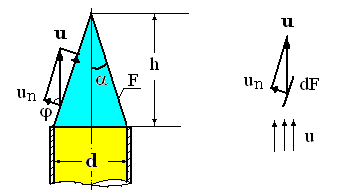
Fig. 4 Conul frontului flacarii laminare la iesirea

amestecului gazelor combustibile din tub

Conform teoriei lui Gouy-Michelson, viteza normala de propagare a frontului de flacara va fi data de relatia care asigura echilibrul suprafetei elementare dF, conform figurii 4:

. (52)

Se poate scrie

, (56)

Pe baza relatiei (56), se poate determina viteza normala de propagare a frontului de flacara, folosind metoda becului Bunssen.

In figura 6 se prezinta variatia vitezei normale de propagare a frontului de flacara in amestecul de gaz metan si aer in functie de temperatura si concentratie.

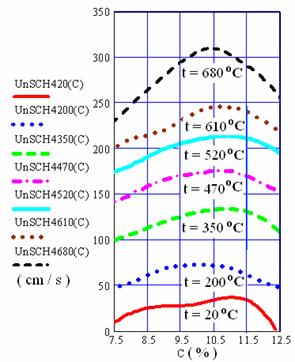
Fig. 6 Variatia vitezei normale de propagare a frontului de flacara a

amestecului de CH₄ cu aer in functie de concentratie si teemperatura

Din analiza graficelor din figura 6 se constata ca la o crestere a temperaturii amestecului de la 20 C la 680 , viteza normala maxima de propagare a frontului de flacara a gazului metan creste de peste zece ori, adica de la 29 cm/s la 315 cm/s,

4.2 Viteza de propagare a frontului de flacara la curgerea turbulenta in cazul arderii combustibililor gazosi

Pentru cazul curgerii cu scara mare a turbulentei ( fiind grosimea frontului de flacara), pentru determinarea vitezei turbulente de propagare a frontului de flacara se poate utiliza relatia:

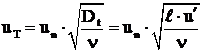, (60)

in care:

D_t - este coeficientul turbulent de difuzie, iar n coeficientul de vascozitate cinematica a amestecului;

- scara turbulentei.

O formula similara cu (60), pentru cazul curgerii cu scara mica a turbulentei este luat in calcul si schimbul molecular de masa:

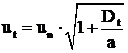, (62)

5 Limitele de aprindere in amestecurile diverselor gaze cu aer si cu oxigen la presiunea atmosferica si temperatura de 293 K

Propagarea flacarii este posibila intre limite determinate de concentratie a combustibilului in amestec (tabelul 1) [35, 63, 115].

Tabelul 1

6 Influenta temperaturii initiale

Viteza de propagare a frontului de flacara depinde de temperatura initiala a amestecului si temperatura gazelor T, conform relatiei:

,    (66)

Variatia lungimii flacarii se calculeaza cu elatia:

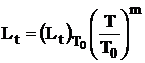, (67)

Variatia temperaturii gazelor de ardere se exprima astfel:

, (69)

7 Influenta presiunii

Viteza de reactie depinde de presiune, conform legii exponentiale in care n este gradul reactiei. Daca se tine seama de relatia (exprima viteza de reactie in functie de presiune, la temperatura constanta, pentru substante care reactioneaza in concentratii volumetrice relative), rezulta [35, 63, 115]:

(69)

Viteza normala masica de ardere este:

.         (70)

In cazul combustibilului format dintr-un amestec de gaze, viteza normala de propagare a frontului de flacara se determina cu relatia:

. (73)

in care x₁, x_k , reprezinta participatiile componentelor, iar u₁ u_k vitezele normale de propagare a frontului de flacara pentru componente.

8 Influenta fluctuatiilor turbulentei asupra vitezei de propagare   a flacarilor amestecurilor omogene combustibil - aer

Viteza de propagare a flacarilor turbulente se determina ca functie de parametrii initiali: compozitia amestecului, presiunea si temperatura initiala, turbulenta initiala a curentului in miscre.

Pentru :,

: ,

rezulta urmatoarele valori numerice si reprezentari grafice:

Fig. 7 Variatia vitezei de ardere laminara a hidrogenului in functie de

coeficientul de dozaj

Fig. 8 Variatia vitezei de ardere laminara a gazului metan in functie de

coeficientul de dozaj

Determinarea ecuatiei de regresie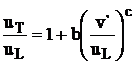

Se aplica metoda celor mai mici patrate pentru determinarea coeficientilor b si c. Se aplica urmatorul algoritm:

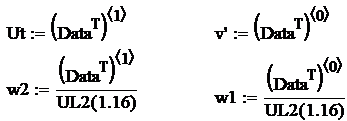
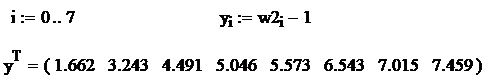
Se logaritmeaza relatia si se fac notatiile:

,

Rezulta: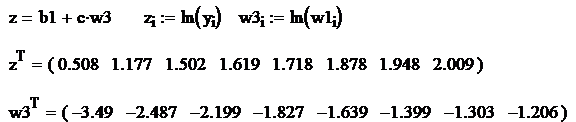

Ecuatia de regresie 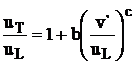ia forma: , care permite determinarea vitezei turbulente la arderea gazului metan in functie de viteza laminara de ardere si de fluctuatia turbulentei.

Reprezentarea grafica a ecuatiei de regresie se efectuiaza pentru valorile relative ale fluctuatiilor:

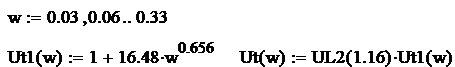
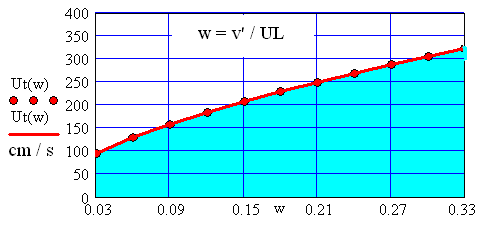
Fig. 9 Variatia vitezei turbulente a gazului metan in functie de fluctuatia

Relativa a turbulentei