Rezolvarea unor probleme cu plati esalonate

Rezolvarea unor probleme cu plati esalonate

1.    Cu 10 ani inaite de a iesi la pensie, o persoana depune cate 700 u. m., la sfarsitul fiecarui an, cu procentul de 5%. Care este valoare fondului acumulat, si ce suma de bani va primii tot restul vietii, la inceputul fiecarui an cu procentul de 4%.

REZOLVARE:

plati esalonate anuale, limitate, posticipate

= T * S_n = T * , unde u = 1+i

p = 100 i => i = = 0,05

u = 1+0,05=1,05

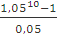= 700 * = 700 * = 700 * 12,58 = 8806

plati esalonate anuale, imediate, nelimitate, anticipate

= T * u * => T =

A_n = T * , unde v = = = 0,95

A₁₀ = 700 * 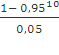= 700 * = 700 * 8,02 = 5614

T = = = = 8806 / 26 = 338,69 u.m.

2.    De ce suma va dispune o persoana daca depune timp de 8 ani, la inceputul fiecarui an, cate 800 u.m. cu procentul de 9% .Care este valoarea actuala a acestor plasamente? Dar daca plasamentele au loc la sfarsitul anului?

REZOLVARE:

a)     plati esalonate anuale, imediate, anticipate, limitate

= T * u * a_n unde a_n =

p = 100 * i => i = = 0,09

u = 1+ i = 1 + 0,09 = 1,09

v = = = = 0,92

= 800 * 1,09 * = 800 * 1,09 * 5,41 = 4717,52

= 4717,52

b)    plati esalonate anuale, imediate, limitate, posticipate

= T * a_n unde a_n =

p = 100*i => i = p/100 = 0,09

v = = = 0,917

= 800 * 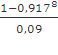= 800 * 5,55 = 4440

= 4440

3.    O datorie a unei persoane a fost esalonata pe timp de 20 de ani cu incepere peste 4 ani, platind anual la inceputul fiecarui an, suma de 6000 u.m. cu procentul de 8%. Care este valoarea datoriei esalonate si care este valoarea finala a acesteia la sfarsitul achitarii ei?

REZOLVARE:

a)     plati esalonate anuale, limitate, amanate, anticipate

= T * u * v^r * a_n-r unde u = 1 + i = 1 + 0,08 = 1,08

p = 100 * i => i = = 0,08

v = = = 0,926

a_n-r = = = = 8,875

=6000 * 1,08 * 0,926⁴ * 8,875=6000* 1,08 * 0,735 * 8,875=42269,85

= 42269,85

b)   

= T * u * s_n-r = T * u *

unde u = 1 + i = 1 + 0,08 = 1,08

p = 100 * i => i = = 0,08

s_n-r = = = = 30,325

= 6000 * 1,08 * 30,325 = 196506

= 196506